Bài tập 21 trang 67 SGK Hình học 12 NC

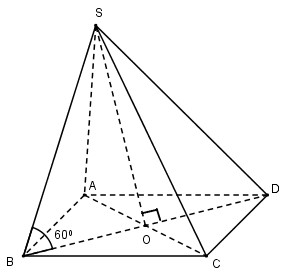
Bán kính đường tròn đáy của hình nón ngoại tiếp hình chóp là

\(\eqalign{
& R = {{a\sqrt 2 } \over 2} \cr 
& \cos {60^0} = {{BO} \over {SB}} \cr 
& \Rightarrow SB = {{BO} \over {\cos {{60}^0}}} = 2{{a\sqrt 2 } \over 2} = a\sqrt 2 \cr} \)

Diện tích xung quanh hình nón \({S_{xq}} = {1 \over 2}.2\pi Rl \) \(= \pi {{a\sqrt 2 } \over 2}a\sqrt 2  = \pi {a^2}\)

Diện tích hình tròn đáy hình nón là \({S_d} = \pi {R^2} = \pi {{{a^2}} \over 2}\)

Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_d} = \pi {a^2} + {{\pi {a^2}} \over 2} = {{3\pi {a^2}} \over 2}\)

Chọn (A).

-- Mod Toán 12 HỌC247