Bài tập 6 trang 65 SGK Hình học 12 NC

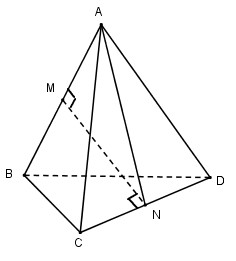
Gọi \(M, N\) lần lượt là trung điểm hai cạnh \(AB\) và \(CD\) của tứ diện đều \(ABCD\).

\(I\) là trung điểm của \(MN\) thì \(I\) cách đều \(6\) cạnh tứ diện nên \(I\) là tâm mặt cầu tiếp xúc với các cạnh của tứ diện đều.

Bán kính mặt cầu: \(R = {{MN} \over 2}\)

Ta có: \(M{N^2} = A{N^2} - M{A^2} \) \(= A{D^2} - N{D^2} - M{A^2}\) \( = {a^2} - {{{a^2}} \over 4} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \)

\(\Rightarrow MN = {{a\sqrt 2 } \over 2} \Rightarrow R = {{a\sqrt 2 } \over 4}\).

Chọn (B).

-- Mod Toán 12 HỌC247