Bài tập 5 trang 64 SGK Hình học 12 NC

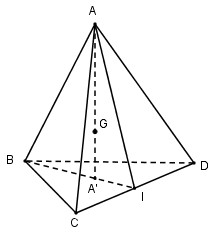
Gọi G là trọng tâm tứ diện ABCD, AA′ là đường cao xuất phát từ A của tứ diện ABCD. Ta có:

\(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)

\(\begin{array}{l}
 \Leftrightarrow {\left( {\overrightarrow {GA}  - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GB}  - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GC}  - \overrightarrow {GM} } \right)^2}\\
 + {\left( {\overrightarrow {GD}  - \overrightarrow {GM} } \right)^2} = 2{a^2}\\
 \Leftrightarrow 4G{A^2} + 4G{M^2} - 2\overrightarrow {GM} \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} } \right) = 2{a^2}\\
 \Leftrightarrow M{G^2} = \frac{{{a^2}}}{2} - G{A^2} = \frac{{{a^2}}}{8}\\
 \Rightarrow MG = \frac{{a\sqrt 2 }}{4}
\end{array}\)

Tập hợp các điểm M là mặt cầu tâm G bán kính \(\frac{{a\sqrt 2 }}{4}\).

Chọn (B).

-- Mod Toán 12 HỌC247