Giải bài 11 tr 53 sách GK Toán Hình lớp 12
Cho hình trụ có bán kính r; O, O' là tâm của hai đáy OO' = 2r. Một mặt cầu (S) tiếp xúc với đáy của hình trụ tại O và O'. Trong các mệnh đề dưới đây, mệnh đề nào sai?
(A) Diện tích mặt cầu bằng diện tích xung quanh của hình trụ;
(B) Diện tích mặt cầy bằng \(\frac{2}{3}\) diện tích toàn phần của hình trụ;
(C) Thể tích khối cầu bằng \(\frac{3}{4}\) thể tích khối trụ;
(D) Thể tích khối cầu bằng \(\frac{2}{3}\) thể tích khối trụ;
Gợi ý trả lời bài 11
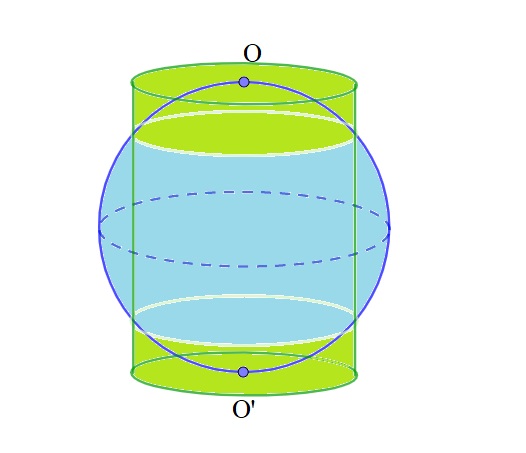
Mặt cầu có đường kính \(\displaystyle 2r\) nên có bán kính là \(\displaystyle r\) và có diện tích:
\(\displaystyle S = 4\pi {r^2}\) và \(\displaystyle V = {4 \over 3}\pi {r^3}\)
Mặt trụ có bán kính \(\displaystyle r\) và chiều cao \(\displaystyle 2r\) nên có:
\(\displaystyle {S_{xq}} = 2\pi rh = 2\pi .r.2r = 4\pi {r^2}\);
\(\displaystyle {S_{tp}}=S_{xq}+S_{2d}=4\pi {r^2} + 2\pi r^2 = 6\pi {r^2}\);
\(\displaystyle V =\pi r^2h=\pi .r.2r= 2\pi {r^3}\).
Do đó A, B, D đúng.
Chọn (C).
-- Mod Toán 12 HỌC247
-


Tính bán kính mặt cầu tiếp xúc với các cạnh của tứ diện đều \(ABCD\) cạnh bằng \(a\) là:
bởi Nguyen Ngoc
 07/06/2021
07/06/2021
(A) \({{a\sqrt 2 } \over 2}\)
(B) \({{a\sqrt 2 } \over 4}\)
(C) \(a\sqrt 2 \)
(D) \(2a\sqrt 2 \)
Theo dõi (0) 1 Trả lời -


Tứ diện đều \(ABCD\) có cạnh bằng \(a\). Tập hợp các điểm \(M\) sao cho \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)
bởi Nguyễn Trà Giang
 06/06/2021
06/06/2021
(A) Mặt cầu có tâm là trọng tâm của tam giác \(ABC\) và bán kính bằng \({{a\sqrt 2 } \over 2}\).
(B) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \({{a\sqrt 2 } \over 4}\).
(C) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \({{a\sqrt 2 } \over 2}\).
(D) Mặt cầu có tâm là trọng tâm của tam giác \(ABC\) và bán kính bằng \({{a\sqrt 2 } \over 4}\).
Theo dõi (0) 1 Trả lời -


(A) Hình chóp có đáy là tứ giác thì có mặt cầu ngoại tiếp.
(B) Hình chóp có đáy là hình thang vuông thì có mặt cầu ngoại tiếp.
(C) Hình chóp có đáy là hình bình hành thì có mặt cầu ngoại tiếp.
(D) Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
Theo dõi (0) 1 Trả lời -


Cho một hình cầu có thể tích \({4 \over 3}\pi \) ngoại tiếp một hình lập phương. Trong các số sau đây, số nào là thể tích khối lập phương?
bởi Mai Trang
 07/06/2021
07/06/2021
(A) \({{8\sqrt 3 } \over 9}\)
(B) \({8 \over 3}\)
(C) 1
(D) \(2\sqrt 3 \)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 9 trang 52 SGK Hình học 12
Bài tập 10 trang 52 SGK Hình học 12
Bài tập 12 trang 53 SGK Hình học 12
Bài tập 13 trang 53 SGK Hình học 12
Bài tập 14 trang 53 SGK Hình học 12
Bài tập 15 trang 54 SGK Hình học 12
Bài tập 16 trang 54 SGK Hình học 12
Bài tập 17 trang 54 SGK Hình học 12
Bài tập 18 trang 54 SGK Hình học 12
Bài tập 2.25 trang 62 SBT Hình học 12
Bài tập 2.26 trang 62 SBT Hình học 12
Bài tập 2.27 trang 62 SBT Hình học 12
Bài tập 2.28 trang 62 SBT Hình học 12
Bài tập 2.29 trang 63 SBT Hình học 12
Bài tập 2.30 trang 63 SBT Hình học 12
Bài tập 2.31 trang 63 SBT Hình học 12
Bài tập 2.32 trang 63 SBT Hình học 12
Bài tập 2.33 trang 64 SBT Hình học 12
Bài tập 2.34 trang 64 SBT Hình học 12
Bài tập 2.35 trang 64 SBT Hình học 12
Bài tập 2.36 trang 64 SBT Hình học 12
Bài tập 2.37 trang 64 SBT Hình học 12
Bài tập 3.38 trang 64 SBT Hình học 12
Bài tập 2.39 trang 65 SBT Hình học 12
Bài tập 2.40 trang 65 SBT Hình học 12
Bài tập 2.41 trang 65 SBT Hình học 12
Bài tập 2.42 trang 65 SBT Hình học 12
Bài tập 2.43 trang 65 SBT Hình học 12
Bài tập 2.44 trang 66 SBT Hình học 12
Bài tập 2.45 trang 66 SBT Hình học 12
Bài tập 2.46 trang 66 SBT Hình học 12
Bài tập 2.47 trang 66 SBT Hình học 12
Bài tập 2.48 trang 66 SBT Hình học 12
Bài tập 2.49 trang 66 SBT Hình học 12
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 63 SGK Hình học 12 NC
Bài tập 3 trang 63 SGK Hình học 12 NC
Bài tập 4 trang 63 SGK Hình học 12 NC
Bài tập 5 trang 63 SGK Hình học 12 NC
Bài tập 6 trang 63 SGK Hình học 12 NC
Bài tập 1 trang 63 SGK Hình học 12 NC
Bài tập 2 trang 64 SGK Hình học 12 NC
Bài tập 3 trang 64 SGK Hình học 12 NC
Bài tập 4 trang 64 SGK Hình học 12 NC
Bài tập 5 trang 64 SGK Hình học 12 NC
Bài tập 6 trang 65 SGK Hình học 12 NC
Bài tập 7 trang 65 SGK Hình học 12 NC
Bài tập 8 trang 65 SGK Hình học 12 NC
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 10 trang 65 SGK Hình học 12 NC
Bài tập 11 trang 66 SGK Hình học 12 NC
Bài tập 12 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 14 trang 66 SGK Hình học 12 NC
Bài tập 15 trang 66 SGK Hình học 12 NC
Bài tập 16 trang 67 SGK Hình học 12 NC
Bài tập 17 trang 67 SGK Hình học 12 NC
Bài tập 18 trang 67 SGK Hình học 12 NC
Bài tập 19 trang 67 SGK Hình học 12 NC
Bài tập 20 trang 67 SGK Hình học 12 NC
Bài tập 21 trang 67 SGK Hình học 12 NC
Bài tập 22 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 24 trang 68 SGK Hình học 12 NC





