Bài tập 11 trang 66 SGK Hình học 12 NC
Một hình trụ có bán kính đáy bằng a, đường cao \({\rm{OO}}' = a\sqrt 3 \). Một đoạn thẳng AB thay đổi sao cho góc giữa AB và trục hình trụ bằng 300. A, B thuộc hai đường tròn đáy của hình trụ. Tập hợp các trung điểm I của AB là:
(A) Một mặt trụ
(B) Một mặt cầu
(C) Một đường tròn
(D) Một mặt phẳng.
Hướng dẫn giải chi tiết
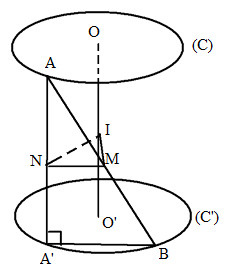
Gọi A′ là hình chiếu của A xuống mặt phẳng đáy thì AA′ = OO′. Gọi I, M, N lần lượt là trung điểm của OO′, AB và AA′.
Ta có: IA = IB và \(IM \bot AB\).
Mp(IMN) qua I và song song với hai mặt phẳng đáy.
Ta có:
\(\begin{array}{l}
MN = AN.\tan {30^0} = \frac{{a\sqrt 3 }}{2}.\frac{1}{{\sqrt 3 }} = \frac{a}{2}\\
\Rightarrow MI = \sqrt {N{I^2} - M{N^2}} \\
= \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}
\end{array}\)
Vậy tập hợp trung điểm M của AB là đường tròn tâm I bán kính \(\frac{{a\sqrt 3 }}{2}\) nằm trong mp(IMN).
Chọn (C).
-- Mod Toán 12 HỌC247
-


Cái ca đựng được bao nhiêu lít nước biết cái ca hình trụ không nắp, đường kính bằng độ cao của cái ca là 10cm?
bởi Hạnh Tồ
 05/11/2019
Một cái ca hình trụ không nắp, đường kính bằng độ cao của cái ca là 10cm. Hỏi cái ca đựng được bao nhiêu lít nướcTheo dõi (0) 5 Trả lời
05/11/2019
Một cái ca hình trụ không nắp, đường kính bằng độ cao của cái ca là 10cm. Hỏi cái ca đựng được bao nhiêu lít nướcTheo dõi (0) 5 Trả lời -


Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC là ?
bởi Trần Quốc Hưng
 28/10/2019
Cho tứ diện S.ABC có cạnh a. S xung quanh của hình nón đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC là ?Theo dõi (0) 7 Trả lời
28/10/2019
Cho tứ diện S.ABC có cạnh a. S xung quanh của hình nón đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC là ?Theo dõi (0) 7 Trả lời -


Tìm tập hợp các điểm M thỏa mãn MA^2+MB^2+2MC^2=12
bởi Nguyễn Nhi
 20/10/2019
Giúp mình câu 43 giải chi tiết nhé
20/10/2019
Giúp mình câu 43 giải chi tiết nhé Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tính thể tích của khối trụ có bán kính đáy r=a và thiết diện đi qua trục là một hình vuông
bởi Lan Ngoc
 22/06/2019
Câu 2
22/06/2019
Câu 2 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 9 trang 65 SGK Hình học 12 NC
Bài tập 10 trang 65 SGK Hình học 12 NC
Bài tập 12 trang 66 SGK Hình học 12 NC
Bài tập 13 trang 66 SGK Hình học 12 NC
Bài tập 14 trang 66 SGK Hình học 12 NC
Bài tập 15 trang 66 SGK Hình học 12 NC
Bài tập 16 trang 67 SGK Hình học 12 NC
Bài tập 17 trang 67 SGK Hình học 12 NC
Bài tập 18 trang 67 SGK Hình học 12 NC
Bài tập 19 trang 67 SGK Hình học 12 NC
Bài tập 20 trang 67 SGK Hình học 12 NC
Bài tập 21 trang 67 SGK Hình học 12 NC
Bài tập 22 trang 68 SGK Hình học 12 NC
Bài tập 23 trang 68 SGK Hình học 12 NC
Bài tập 24 trang 68 SGK Hình học 12 NC





