Bài tập 1 trang 43 SGK Giải tích 12

Phương pháp giải:

Trước khi giải bài 1, ta cùng ôn lại các bước khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 3:

- Tập xác định: \(D=\mathbb{R}.\)

- Sự biến thiên: Xét chiều biến thiên của hàm số

+ Tính đạo hàm: \(y' = 3{\rm{a}}{{\rm{x}}^{\rm{2}}}{\rm{ + 2bx + c}}\)

​​+ \(y' = 0 \Leftrightarrow 3{\rm{a}}{{\rm{x}}^{\rm{2}}}{\rm{ + 2bx + c = 0}}\) (Bấm máy tính nếu nghiệm chẵn, giải \(\Delta ;\Delta '\) nếu nghiệm lẻ - không được ghi nghiệm gần đúng).

+ Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.

- Tìm cực trị

- Tìm các giới hạn tại vô cực (\(x \to \pm \infty\))

- Hàm số bậc ba nói riêng và các hàm số đa thức nói chung không có tiệm cận đứng và tiệm cận ngang.

- Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.

- Đồ thị:

+ Tính đối xứng: Đồ thị hàm số bậc ba nhận điểm \(I(x_0,f(x_0))\) với \(x_0\) là nghiệm phương trình \(f''(x_0)=0\) làm tâm đối xứng.

+ Giao của đồ thị với trục Oy: x=0 =>y=d => (0; d)

+ Giao của đồ thị với trục Ox: \(y = 0 \Leftrightarrow {\rm{a}}{{\rm{x}}^{\rm{3}}}{\rm{ + b}}{{\rm{x}}^{\rm{2}}}{\rm{ + cx + d}} = 0 \Leftrightarrow x = ?\)

+ Các điểm CĐ; CT (nếu có).

+ Lấy thêm một số điểm (nếu cần), điều này làm sau khi hình dung hình dạng của đồ thị. Thiếu bên nào học sinh lấy điểm phía bên đó, không lấy tùy tiện mất thời gian.

Trong thực tế, khi giải bài tập để thuận lợi cho việc tính toán ta thường tính giới hạn, lập bảng biến thiên rồi mới suy ra cực trị của hàm số.

Lời giải:

Áp dụng ta tiến hành giải câu a, b, c, d bài 1 như sau:

Câu a:

Xét hàm số y = 2 + 3x - x³

Tập xác định: \(D=\mathbb{R}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)

Sự biến thiên:

Đạo hàm: y' = 3 - 3x² .

Ta có: y' = 0 ⇔ x = ± 1 .

Bảng biến thiên:

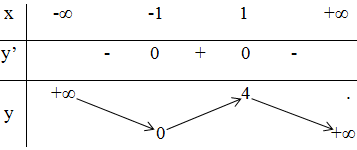
Vậy hàm số đồng biến trên các khoảng (-1;1), nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right).\)

Cực trị: Hàm số đạt cực đại tại x = 1, giá trị cực đại y_CĐ = y(1) = 4, đạt cực tiểu tại x = -1 và y_CT = y(-1) = 0.

Đồ thị:

Ta có: y'' = -6x; y'' = 0 ⇔ x = 0. Với x = 0 ta có y = 2. Vậy đồ thị hàm số nhận điểm I(0;2) làm tâm đối xứng.

Đồ thị cắt trục Ox tại các điểm (2;0) và (-1;0), cắt Oy tại điểm (0;2).

Đồ thị hàm số nhận điểm (0;2) làm điểm uốn. 

Nhận thấy, nhánh bên trái vẫn còn thiếu một điểm để vẽ đồ thị, dựa vào tính đối xứng ta chọn điểm của hoành độ x = -2 suy ra y = 4.

Câu b:

Xét hàm số y = x³ + 4x² + 4x

Tập xác định: \(D=\mathbb{R}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).

Sự biến thiên:

Đạo hàm: y' = 3x² + 8x + 4.

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l} x = - 2\\ x = - \frac{2}{3} \end{array} \right.\)

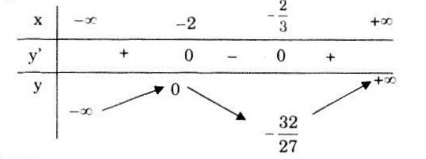
Bảng biến thiên:

Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - \frac{2}{3}; + \infty } \right)\) và nghịch biến trên \(\left( { - 2; - \frac{2}{3}} \right).\)

Cực trị:

Hàm số đạt cực đại tại x=-2, giá trị cực đại y_cđ = y(-2) = 0.

Hàm số đạt cực tiểu tại \(x=-\frac{2}{3}\), giá trị cực tiểu \(y_{ct}=y\left ( -\frac{2}{3} \right )=-\frac{32}{27}.\)

Đồ thị hàm số:

Tâm đối xứng của đồ thị hàm số: \(y''=6x+8;\)\(y''=0\Leftrightarrow x=-\frac{4}{3}\Rightarrow y=-\frac{16}{27}.\) 

Đồ thị hàm số cắt trục Oy tại điểm (0;0), cắt trục Ox tại điểm có hoành độ là nghiệm của phương trình: x³ + 4x² + 4x = 0 ⇔ x = 0 hoặc x = -2 nên tọa độ các giao điểm là (0;0) và (-2;0).

Câu c:

Xét hàm số \(\small y = x^3 + x^2+ 9x\)

Tập xác định: \(D=\mathbb{R}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = + \infty\).

Sự biến thiên:

Đạo hàm: y' = 3x² + 2x + 9 > 0, ∀x.

Vậy hàm số luôn đồng biến trên \(\mathbb{R}\) và không có cực trị.

Bảng biến thiên :

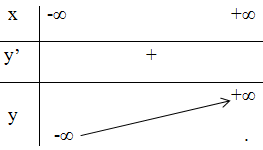
Đồ thị:

Đồ thị hàm số cắt trục Ox tại điểm (0;0), cắt trục Oy tại điểm (0;0).

Đồ thị hàm số có tâm đối xứng là điểm có hoành độ là nghiệm của phương trình y'' = 0 ⇔ 6x+2 = 0 ⇔ \(x=-\frac{1}{3}.\) Suy ra tọa độ tâm đối xứng là: \(I\left ( -\frac{1}{3};-\frac{79}{27} \right ).\)

Lúc này ta vẫn chưa có đủ điểm để vẽ đồ thị hàm số, ta cần lấy thêm hai điểm có hoành độ cách đều hoành độ \(x_1\) và \(x_2\) sao cho \(\left| {{x_1} - \left( { - \frac{1}{3}} \right)} \right| = \left| {{x_2} - \left( { - \frac{1}{3}} \right)} \right|\), khi đó hai điểm này sẽ đối xứng nhau qua điểm uốn. Ta chọn các điểm (-1;-9) và \(\left ( \frac{1}{2};\frac{39}{8} \right ).\)

Câu d:

Xét hàm số y=-2x³+5

Tập xác định: \(D=\mathbb{R}.\)

Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to + \infty } y = - \infty\)

Sự biến thiên:

Đạo hàm: y' = -6x² ≤ 0, ∀x.

Bảng biến thiên:

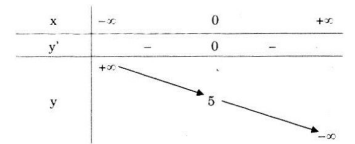
Vậy hàm số luôn nghịch biến trên R.

Hàm số không có cực trị.

Đồ thị:

Tính đối xứng: y'' = -12x; y'' = 0 ⇔ x = 0. Vậy đồ thị hàm số nhận điểm uốn I(0;5) làm tâm đối xứng.

Đồ thị hàm số cắt trục Oy tại điểm (0;5), đồ thị cắt trục Ox tại điểm \(\left( {\sqrt[3]{{\frac{5}{2}}};0} \right).\) 

-- Mod Toán 12 HỌC247