Bài tập 1.64 trang 37 SBT Toán 12

a)

Tập xác định : \(D = R\)

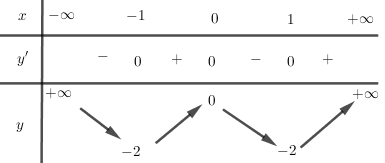
\(y' = 8{x^3} - 8x = 8x({x^2} - 1)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 0\\x = 1\end{array} \right.\)

Hàm số đồng biến trên mỗi khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\)

Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\)

Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = 0\)

Hàm số đạt cực tiểu tại \(x =  \pm 1;{y_{CT}} =  - 2\)

Giới hạn: \(\mathop {\lim }\limits_{x \to  \pm \infty } y =  + \infty \)

\(y'' = 24{x^2} - 8;\)\(y'' = 0 \Leftrightarrow {x^2} = \dfrac{1}{3} \Leftrightarrow x =  \pm \dfrac{{\sqrt 3 }}{3}\)

Đồ thị có hai điểm uốn:  \({I_1}\left( { - \dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right);\)\({I_2}\left( {\dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right)\).

Bảng biến thiên:

Đồ thị:

Đồ thị cắt trục hoành tại: \(A\left( { - \sqrt 2 ;0} \right),O\left( {0;0} \right),B\left( {\sqrt 2 ;0} \right)\)

b)

Ta có: \({x^2}|{x^2} - 2| = m\)\( \Leftrightarrow 2{x^2}\left| {{x^2} - 2} \right| = 2m\)\( \Leftrightarrow \left| {2{x^2}\left( {{x^2} - 2} \right)} \right| = 2m\)\( \Leftrightarrow \left| {2{x^4} - 4{x^2}} \right| = 2m\)

Từ đồ thị hàm số \(y = 2{x^4}-4{x^2}\) có thể suy ra đồ thị của hàm số \(y = \left| {2{x^4} - 4{x^2}} \right|\) như sau:

Phương trình : \(\left| {2{x^4} - 4{x^2}} \right| = 2m\)  có \(6\) nghiệm phân biệt khi và chỉ khi đường thẳng \(y = 2m\) giao với đồ thị trên tại \(6\) điểm phân biệt \( \Leftrightarrow 0 < 2m < 2\) \( \Leftrightarrow 0 < m < 1\).

Vậy \(0 < m < 1\).

-- Mod Toán 12 HỌC247