Giải bài 1.68 tr 38 SBT Toán 12
Hàm số \(y = {x^3} + (m + 3){x^2} + mx - 2\) đạt cực tiểu tại x = 1. Khi :
A. m = 1
B. m = 2
C. m =−3
D. m = 4
Hướng dẫn giải chi tiết
Ta có:
\(y' = 3{x^2} + 2(m + 3)x + m\)
\(y'' = 6x + 2(m + 3)\)
Vì hàm số đạt cực tiểu tại nên ta có:
\(y'(1) = 3 + 2(m + 3) + m = 0 \)
\(\Leftrightarrow 3m + 9 = 0 \Leftrightarrow m = - 3\)
Với ta có:
\(y'' = 6x \Rightarrow y''(1) = 6 > 0\)
Thỏa mãn, vậy với hàm số đạt cực tiểu tại
Đáp án: C
-- Mod Toán 12 HỌC247
-

 Kiểm tra học ki 1 lớp 12 đề ôn số 4
Kiểm tra học ki 1 lớp 12 đề ôn số 4 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm các khẳng định đúng biết y=(x-1)/(x+1)?
bởi Nguyễnn Linhh
 26/12/2019
Giúp e câu 15 với ạ
26/12/2019
Giúp e câu 15 với ạ Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Khảo sát sự biến thiên và vẽ đồ thị hàm số y= 2x-1/x-1Theo dõi (0) 0 Trả lời
Khảo sát sự biến thiên và vẽ đồ thị hàm số y= 2x-1/x-1Theo dõi (0) 0 Trả lời -


Đồ thị hình bên là của hàm số nào?
bởi Nguyễnn Linhh
 22/12/2019
Giải như thế nào v ạ
22/12/2019
Giải như thế nào v ạ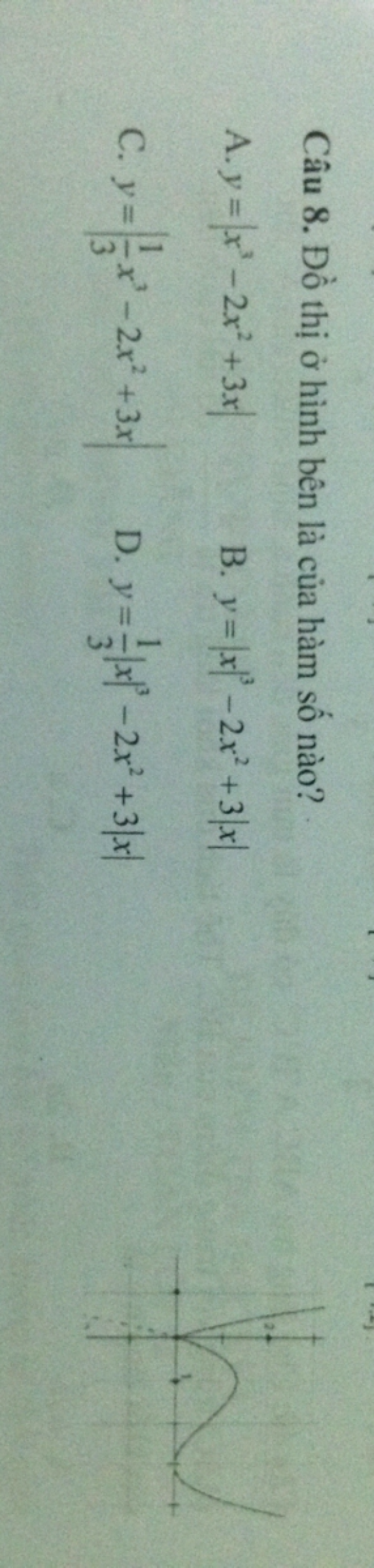 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -

 Câu 22
Câu 22 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Phương trình f(x) < căn(x^2+e)+m nghiệm đúng với mọi x thuộc (-3;-1) khi và chỉ khi?
bởi Yaya Moua
 21/12/2019
21/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tất cả các giá trị thực của m để hàm số y=(mx+4)/(x+m) nghịch biến trên khoảng (-vô cực;1)
bởi Nguyễn Ngọc Ly
 18/12/2019
.
18/12/2019
. Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.66 trang 38 SBT Toán 12
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.69 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC





