Giải bài 1.69 tr 38 SBT Toán 12
Hàm số \(y = {x^4} + ({m^2} - 4){x^2} + 5\) có ba cực trị khi :
A.
B.
C.
D.
Hướng dẫn giải chi tiết
\(\begin{array}{l}
y' = 4{x^3} + 2({m^2} - 4)x\\
\Rightarrow y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{{x^2} = - \frac{{{m^2} - 4}}{2}}
\end{array}} \right.
\end{array}\)
Để đồ thị hàm số có ba cực trị thì phương trình có ba nghiệm phân biệt, hay:
\( - \frac{{{m^2} - 4}}{2} > 0 \Leftrightarrow - 2 < m < 2\)
Chọn A
-- Mod Toán 12 HỌC247
-


Hàm số y=f(x^2) đồng biến trên khoảng nào dưới đây?
bởi Quốc Ngoan
 17/12/2019
Hàm hợp
17/12/2019
Hàm hợp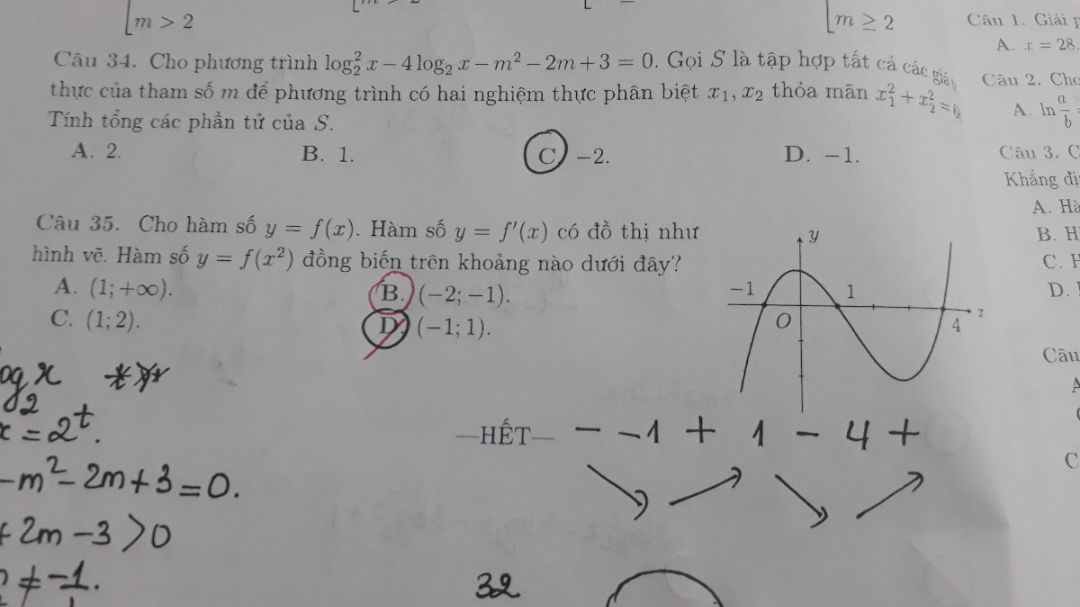 Theo dõi (2) 3 Trả lời
Theo dõi (2) 3 Trả lời -


Đồ thị hàm số y =(2x+1)/(x-1) có tâm đối xứng là?
bởi Thuận Lý
 17/12/2019
Tâm đối xứngTheo dõi (0) 0 Trả lời
17/12/2019
Tâm đối xứngTheo dõi (0) 0 Trả lời -


 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm m để phương trình x^4-2x^2=m có 2nghiệm phân biệt
bởi SiAb's Me'd
 17/12/2019
Cho hàm số y = x^-2x^2-2Theo dõi (0) 0 Trả lời
17/12/2019
Cho hàm số y = x^-2x^2-2Theo dõi (0) 0 Trả lời -


Tìm nghiệm của phương trình 4^x-2^x-12=0
bởi Nguyễn Tuấn Trường
 16/12/2019
Câu 20,21
16/12/2019
Câu 20,21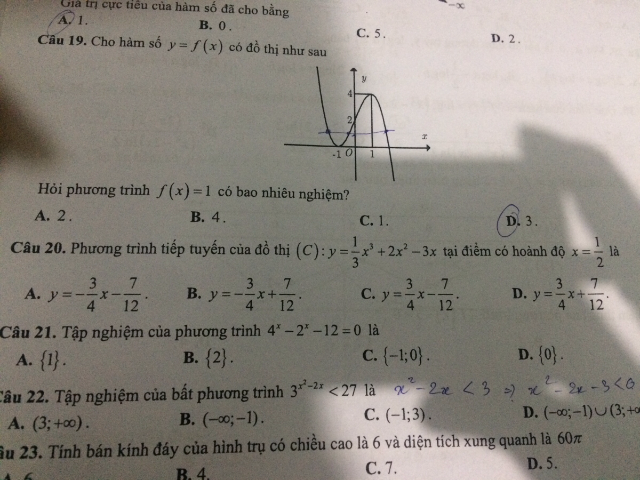 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -

 Bao nhiêu đường tiệm cận z mn
Bao nhiêu đường tiệm cận z mn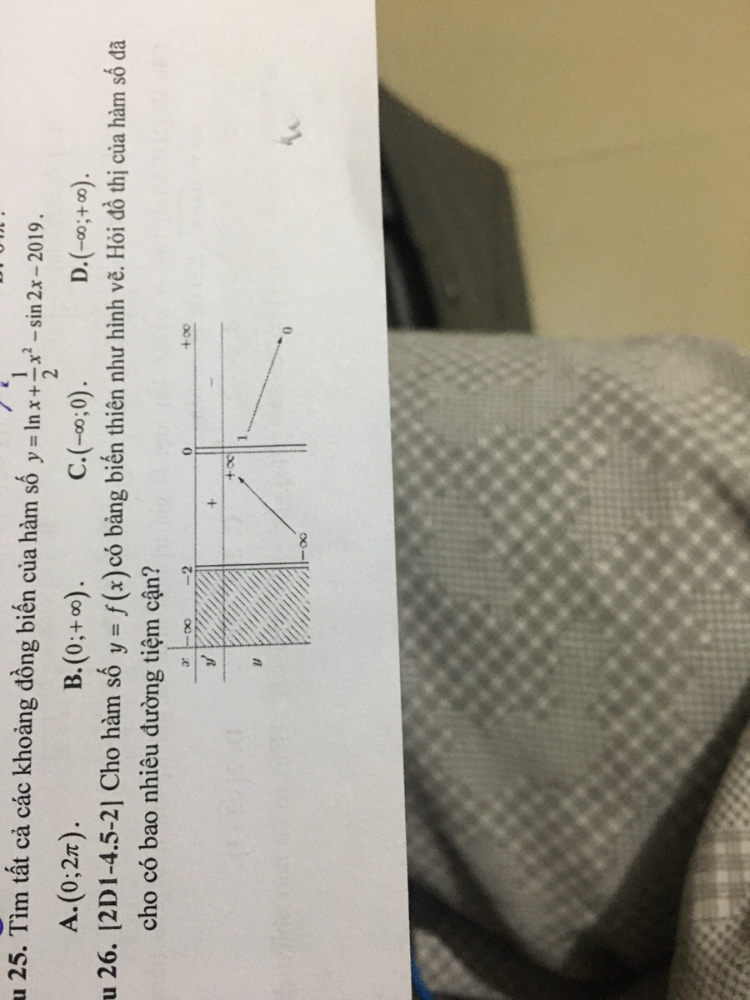 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 1.67 trang 38 SBT Toán 12
Bài tập 1.68 trang 38 SBT Toán 12
Bài tập 1.70 trang 38 SBT Toán 12
Bài tập 1.71 trang 39 SBT Toán 12
Bài tập 1.72 trang 39 SBT Toán 12
Bài tập 1.73 trang 39 SBT Toán 12
Bài tập 1.74 trang 39 SBT Toán 12
Bài tập 29 trang 27 SGK Toán 12 NC
Bài tập 30 trang 27 SGK Toán 12 NC
Bài tập 31 trang 27 SGK Toán 12 NC
Bài tập 32 trang 28 SGK Toán 12 NC
Bài tập 33 trang 28 SGK Toán 12 NC
Bài tập 40 trang 43 SGK Toán 12 NC
Bài tập 41 trang 44 SGK Toán 12 NC
Bài tập 42 trang 45 SGK Toán 12 NC
Bài tập 43 trang 44 SGK Toán 12 NC
Bài tập 44 trang 44 SGK Toán 12 NC
Bài tập 45 trang 44 SGK Toán 12 NC
Bài tập 46 trang 44 SGK Toán 12 NC
Bài tập 47 trang 45 SGK Toán 12 NC
Bài tập 48 trang 45 SGK Toán 12 NC
Bài tập 49 trang 49 SGK Toán 12 NC
Bài tập 50 trang 49 SGK Toán 12 NC
Bài tập 51 trang 49 SGK Toán 12 NC
Bài tập 52 trang 50 SGK Toán 12 NC
Bài tập 53 trang 50 SGK Toán 12 NC
Bài tập 54 trang 50 SGK Toán 12 NC
Bài tập 55 trang 50 SGK Toán 12 NC
Bài tập 56 trang 50 SGK Toán 12 NC
Bài tập 57 trang 55 SGK Toán 12 NC
Bài tập 58 trang 56 SGK Toán 12 NC
Bài tập 59 trang 56 SGK Toán 12 NC
Bài tập 60 trang 56 SGK Toán 12 NC
Bài tập 61 trang 56 SGK Toán 12 NC
Bài tập 62 trang 57 SGK Toán 12 NC
Bài tập 63 trang 57 SGK Toán 12 NC
Bài tập 64 trang 57 SGK Toán 12 NC





