Giải bài 5 tr 26 sách GK Toán Hình lớp 12
Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Hãy tính đường cao OH của hình chóp.
Hướng dẫn giải chi tiết bài 5
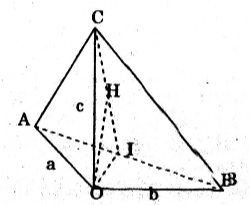
Gọi I là hình chiếu của O lên AB. Vì OC vuông góc với OA và OB nên \(OC\perp (OAB)\Rightarrow OC\perp AB\).
Từ đó ta suy ra: \(AB\perp (COI)\).
Vậy H là hình chiếu của O lên CI.
Trong tam giác vuông AOB ta có:
\(\frac{1}{OI^2}=\frac{1}{OA^2}+\frac{1}{OB^2} \ \ \ (1)\)
Trong tam giác vuông COI ta có: \(\frac{1}{OH^2}=\frac{1}{OI^2}+\frac{1}{OC^2} \ \ (2)\)
Từ (1) và (2) ta có:
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2} + \frac{1}{OC^2} \)
\(= \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
\(=\frac{a^2b^2+b^2c^2+c^2a^2}{a^2b^2c^2}\)
\(\Leftrightarrow OH=\frac{abc}{\sqrt{a^2b^2+b^2c^2+c^2a^2}}\)
Nhận xét: Ta có thể tính OH từ mối liên hệ:
\(V_{O.ABC}=\frac{1}{6}abc=\frac{1}{3}.OH.S_{\Delta ABC}\)
-- Mod Toán 12 HỌC247
-
Hai hình đa diện bằng nhau khi và chỉ khi:
bởi Trần Hoàng Mai
29/05/2020
A. Có phép tịnh tiến biến hình này thành hình kia
B. Có phép dời hình biến hình này thành hình kia
C. Có các cạnh tương ứng bằng nhau
D. Có các mặt tương ứng là các đa giác bằng nhau
Theo dõi (0) 4 Trả lời -
A. Chẵn
B. Lẻ
C. Nhỏ hơn hoặc bằng số đỉnh
D. Lớn hơn hoặc bằng 6
Theo dõi (0) 3 Trả lời -
A. 5 cạnh B. 4 cạnh
C. 3 cạnh D. 2 cạnh
Theo dõi (0) 4 Trả lời -
A. 2 mặt B. 3 mặt
C. 4 mặt D. 5 mặt
Theo dõi (0) 3 Trả lời -
Trong các mệnh đề sau, mệnh đề nào đúng?
bởi Trần Bảo Việt
29/05/2020
A. Mỗi hình đa diện có ít nhất 8 mặt
B. Mỗi hình đa diện có ít nhất 6 mặt
C. Mỗi hình đa diện có ít nhất 5 mặt
D. Mỗi hình đa diện có ít nhất 4 mặt
Theo dõi (0) 3 Trả lời -
Trong các hình sau đây, hình nào là hình đa diện?
bởi Trần Bảo Việt
29/05/2020
Theo dõi (0) 1 Trả lời -
Trong các mệnh đề sau, mệnh đề nào đúng?
bởi Nguyễn Sơn Ca
28/05/2020
A. Trong một hình đa diện tổng của số mặt và số cạnh nhỏ hơn số đỉnh.
B. Trong một hình đa diện tổng của số mặt và số đỉnh lớn hơn số cạnh
C. Trong một hình đa diện tổng số cạnh và số đỉnh nhỏ hơn số mặt
D. Tồn tại một hình đa diện có tổng của số mặt và số đỉnh nhỏ hơn số cạnhTheo dõi (0) 1 Trả lời -
Trong các mệnh đề sau, mệnh đề nào sai ?
bởi Lê Gia Bảo
29/05/2020
A. Tồn tại một hình đa diện có số cạnh bằng 7
B. Tồn tại một hình đa diện có số cạnh nhỏ hơn 7
C. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6
D. Tồn tại một hình đa diện có số cạnh lớn hơn 7
Theo dõi (0) 1 Trả lời
