Giải bài 6 tr 26 sách GK Toán Hình lớp 12
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một góc bằng 600. Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA.
a) Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC
b) Tính thể tích khối chóp S.DBC
Hướng dẫn giải chi tiết bài 6
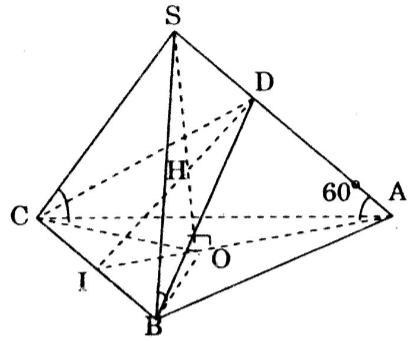
Câu a:
Ta có: AB = BC = CA = a
Gọi O là hình chiều vuông góc của (S) lên (ABC)
Khi đó ta có: \(\widehat{SBO}=\widehat{SCO}=\widehat{SAO}=60^0\)
\(\Rightarrow \Delta SOA=\Delta SOB=\Delta SOC\)
\(\Rightarrow OA=OB=OC\) hay O là tâm của tam giác đều ABC.
Trong các tam giác SOA, SOB, SOC. Ta có:
\(SA=SB=SC=2OA=2.\frac{2}{3}.\frac{a\sqrt{3}}{2}\)
\(=\frac{2a\sqrt{3}}{3}\)
\(SO=\sqrt{SB^2-OB^2}=a\)
Gọi I là trung điểm của BC, ta có: \(ID\perp SA\)
Nên \(ID. SA=SO.IA\)
\(\Rightarrow ID=\frac{a.\frac{a\sqrt{3}}{2}}{\frac{2a\sqrt{3}}{3}}= \frac{3}{4}a\)
Xét tam giác vuông IDA, ta có:
\(DA=\sqrt{IA^2-ID^2}=\frac{a\sqrt{3}}{4}\)
\(\Rightarrow SD=\frac{2a\sqrt{3}}{3}- \frac{a\sqrt{3}}{4}=\frac{5a\sqrt{3}}{12}\)
Mặt khác:
\(\frac{V_{S.ABC}}{V_{S.DBC}}=\frac{V_{S.DBC}+V_{A.BCD}}{V_{SDBC}}= 1+\frac{AD}{SD}\)
\(=1+\frac{\frac{a\sqrt{3}}{4}}{\frac{5a\sqrt{3}}{12}}=\frac{8}{5}\Rightarrow \frac{V_{S.DBC}}{V_{S.ABC}}=\frac{5}{8}\)
Câu b:
Ta có: \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4};SH = AH.\tan {60^0} = a\)
\( \Rightarrow {V_{SABC}} = \frac{1}{3}.SH.{S_{ABC}} = \frac{1}{3}.a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
Từ kết quả câu a) ta có:
\({V_{S.DBC}} = \frac{5}{8}.{V_{S.ABC}} = \frac{5}{8}.\frac{{{a^3}\sqrt 3 }}{{12}} = \frac{{5{a^3}\sqrt 3 }}{{96}}\)
-- Mod Toán 12 HỌC247
-


Cho tứ diện đều ABCD và phép dời hình f biến ABCD thành chính nó, nghĩa là biến mỗi đỉnh của tứ diện thành một đỉnh của tứ diện. Tìm tập hợp các điểm M trong không gian sao cho \(M = f\left( M \right)\) trong trường hợp sau đây: \(\eqalign{ & f\left( A \right) = B,f\left( B \right) = C,f\left( C \right) = A \cr} \)
bởi Thanh Thanh
 06/06/2021
06/06/2021
Cho tứ diện đều ABCD và phép dời hình f biến ABCD thành chính nó, nghĩa là biến mỗi đỉnh của tứ diện thành một đỉnh của tứ diện. Tìm tập hợp các điểm M trong không gian sao cho \(M = f\left( M \right)\) trong trường hợp sau đây: \(\eqalign{ & f\left( A \right) = B,f\left( B \right) = C,f\left( C \right) = A \cr} \)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC và phép dời hình f biến tam giác ABC thành chính nó với \(f\left( A \right) = A,f\left( B \right) = B,f\left( C \right) = C\). Chứng minh f biến mọi điểm M của \(mp\left( {ABC} \right)\) thành chính nó, tức là \(f\left( M \right) = M\).
bởi Suong dem
 06/06/2021
06/06/2021
Cho tam giác ABC và phép dời hình f biến tam giác ABC thành chính nó với \(f\left( A \right) = A,f\left( B \right) = B,f\left( C \right) = C\). Chứng minh f biến mọi điểm M của \(mp\left( {ABC} \right)\) thành chính nó, tức là \(f\left( M \right) = M\).
Theo dõi (0) 1 Trả lời -


Cho hai điểm phân biệt A, B và phép dời hình f biến A thành A, biến B thành B. Chứng minh rằng f biến mọi điểm M nằm trên đường thẳng AB thành chính nó.
bởi Lam Van
 06/06/2021
06/06/2021
Cho hai điểm phân biệt A, B và phép dời hình f biến A thành A, biến B thành B. Chứng minh rằng f biến mọi điểm M nằm trên đường thẳng AB thành chính nó.
Theo dõi (0) 1 Trả lời -


Chứng minh phép dời hình biến một mặt cầu thành một mặt cầu có cùng bán kính.
bởi Bảo Anh
 07/06/2021
07/06/2021
Chứng minh phép dời hình biến một mặt cầu thành một mặt cầu có cùng bán kính.
Theo dõi (0) 1 Trả lời -


Cho hai tứ diện \(ABCD\) và \({A'}{B'}{C'}{D'}\) có các cạnh tương ứng bằng nhau : \(AB = {A'}{B'},BC = {B'}{C'},CD = {C'}{D'},\) \(DA = {D'}{A'},DB = {D'}{B'},AC = {A'}{C'}.\) Chứng minh rằng có không quá một phép dời hình biến các điểm \(A,B,C,D\) lần lượt thành các điểm \({A'},{B'},{C'},{D'}\).
bởi Kieu Oanh
 06/06/2021
06/06/2021
Cho hai tứ diện \(ABCD\) và \({A'}{B'}{C'}{D'}\) có các cạnh tương ứng bằng nhau : \(AB = {A'}{B'},BC = {B'}{C'},CD = {C'}{D'},\) \(DA = {D'}{A'},DB = {D'}{B'},AC = {A'}{C'}.\) Chứng minh rằng có không quá một phép dời hình biến các điểm \(A,B,C,D\) lần lượt thành các điểm \({A'},{B'},{C'},{D'}\).
Theo dõi (0) 1 Trả lời -


Cho tứ diện ABCD. Chứng tỏ rằng phép dời hình biến mỗi điểm A, B, C, D thành chính nó phải là phép đồng nhất.
bởi Đào Thị Nhàn
 07/06/2021
07/06/2021
Cho tứ diện ABCD. Chứng tỏ rằng phép dời hình biến mỗi điểm A, B, C, D thành chính nó phải là phép đồng nhất.
Theo dõi (0) 1 Trả lời -


Phép biến hình biến mỗi điểm M của không gian thành chính nó gọi là phép đồng nhất, thường được kí hiệu là e. Hỏi phép đồng nhất e có phải là phép dời hình hay không?
bởi bala bala
 07/06/2021
07/06/2021
Phép biến hình biến mỗi điểm M của không gian thành chính nó gọi là phép đồng nhất, thường được kí hiệu là e. Hỏi phép đồng nhất e có phải là phép dời hình hay không?
Theo dõi (0) 1 Trả lời -


Mỗi lần cưa, máy cưa có thể cưa một hay nhiều tấm gỗ theo một mặt phẳng. Người ta muốn cưa một khối gỗ hình lập phương thành 27 khối lập phương bằng nhau. Có thể dùng ít hơn 6 lần cưa hay không?
bởi can tu
 07/06/2021
07/06/2021
Mỗi lần cưa, máy cưa có thể cưa một hay nhiều tấm gỗ theo một mặt phẳng. Người ta muốn cưa một khối gỗ hình lập phương thành 27 khối lập phương bằng nhau. Có thể dùng ít hơn 6 lần cưa hay không?
Theo dõi (0) 1 Trả lời -


Khối lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\). Mặt phẳng \(\left( {MB'D'N} \right)\) chia khối lập phương đã cho thành hai khối đa diện. Gọi \(\left( H \right)\) là khối đa diện chứa đỉnh \(A\). Thể tích của khối đa diện \(\left( H \right)\) bằng:
bởi Naru to
 07/06/2021
07/06/2021
A. \(\dfrac{{{a^3}}}{9}\)
B. \(\dfrac{{{a^3}}}{6}\)
C. \(\dfrac{{{a^3}}}{4}\)
D. \(\dfrac{{7{a^3}}}{{24}}\)
Theo dõi (0) 1 Trả lời -


Với hình chóp \(S.ABCD\) có đáy là hình vuông, \(SA\) vuông góc với đáy, \(SA = AC\). Mặt phẳng qua \(A\) vuông góc với \(SC\) cắt \(SB,SC,SD\) lần lượt tại \(B',C',D'\). Tỉ số giữa thể tích hình chóp \(S.AB'C'D'\) và thể tích hình chóp \(S.ABCD\) là:
bởi Minh Thắng
 07/06/2021
07/06/2021
A. \(\dfrac{1}{6}\)
B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{3}\)
D. \(\dfrac{1}{2}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4 trang 26 SGK Hình học 12
Bài tập 5 trang 26 SGK Hình học 12
Bài tập 7 trang 26 SGK Hình học 12
Bài tập 8 trang 26 SGK Hình học 12
Bài tập 9 trang 26 SGK Hình học 12
Bài tập 10 trang 27 SGK Hình học 12
Bài tập 11 trang 27 SGK Hình học 12
Bài tập 12 trang 27 SGK Hình học 12
Bài tập 1 trang 27 SGK Hình học 12
Bài tập 2 trang 27 SGK Hình học 12
Bài tập 3 trang 27 SGK Hình học 12
Bài tập 4 trang 28 SGK Hình học 12
Bài tập 5 trang 28 SGK Hình học 12
Bài tập 6 trang 28 SGK Hình học 12
Bài tập 7 trang 28 SGK Hình học 12
Bài tập 8 trang 28 SGK Hình học 12
Bài tập 9 trang 28 SGK Hình học 12
Bài tập 10 trang 28 SGK Hình học 12
Bài tập 1.18 trang 19 SBT Hình học 12
Bài tập 1.19 trang 19 SBT Hình học 12
Bài tập 1.20 trang 19 SBT Hình học 12
Bài tập 1.21 trang 19 SBT Hình học 12
Bài tập 1.22 trang 19 SBT Hình học 12
Bài tập 1.23 trang 19 SBT Hình học 12
Bài tập 1.24 trang 19 SBT Hình học 12
Bài tập 1.25 trang 19 SBT Hình học 12
Bài tập 1.26 trang 19 SBT Hình học 12
Bài tập 1.27 trang 20 SBT Hình học 12
Bài tập 1.28 trang 20 SBT Hình học 12
Bài tập 1.29 trang 20 SBT Hình học 12
Bài tập 1.30 trang 20 SBT Hình học 12
Bài tập 1.31 trang 20 SBT Hình học 12
Bài tập 1.32 trang 20 SBT Hình học 12
Bài tập 1.33 trang 20 SBT Hình học 12
Bài tập 1.34 trang 20 SBT Hình học 12
Bài tập 1.35 trang 20 SBT Hình học 12
Bài tập 1.36 trang 21 SBT Hình học 12
Bài tập 1.37 trang 21 SBT Hình học 12
Bài tập 1.38 trang 21 SBT Hình học 12
Bài tập 1.39 trang 21 SBT Hình học 12
Bài tập 1.40 trang 21 SBT Hình học 12
Bài tập 1.41 trang 21 SBT Hình học 12
Bài tập 1.42 trang 21 SBT Hình học 12
Bài tập 1.43 trang 21 SBT Hình học 12
Bài tập 1.44 trang 22 SBT Hình học 12
Bài tập 1.45 trang 22 SBT Hình học 12
Bài tập 1.46 trang 22 SBT Hình học 12
Bài tập 1.47 trang 22 SBT Hình học 12
Bài tập 1.48 trang 22 SBT Hình học 12
Bài tập 1.49 trang 22 SBT Hình học 12
Bài tập 1.50 trang 22 SBT Hình học 12
Bài tập 1.51 trang 23 SBT Hình học 12
Bài tập 1.52 trang 23 SBT Hình học 12
Bài tập 1.53 trang 23 SBT Hình học 12
Bài tập 1.54 trang 23 SBT Hình học 12
Bài tập 1.55 trang 23 SBT Hình học 12
Bài tập 1.56 trang 23 SBT Hình học 12
Bài tập 1.57 trang 24 SBT Hình học 12
Bài tập 1.58 trang 24 SBT Hình học 12
Bài tập 1.59 trang 24 SBT Hình học 12
Bài tập 1 trang 30 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 31 SGK Hình học 12 NC
Bài tập 4 trang 31 SGK Hình học 12 NC
Bài tập 5 trang 31 SGK Hình học 12 NC
Bài tập 6 trang 31 SGK Hình học 12 NC
Bài tập 1 trang 31 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 32 SGK Hình học 12 NC
Bài tập 4 trang 32 SGK Hình học 12 NC
Bài tập 5 trang 32 SGK Hình học 12 NC
Bài tập 6 trang 32 SGK Hình học 12 NC
Bài tập 7 trang 32 SGK Hình học 12 NC
Bài tập 8 trang 32 SGK Hình học 12 NC
Bài tập 9 trang 32 SGK Hình học 12 NC
Bài tập 10 trang 32 SGK Hình học 12 NC
Bài tập 11 trang 33 SGK Hình học 12 NC
Bài tập 12 trang 33 SGK Hình học 12 NC
Bài tập 13 trang 33 SGK Hình học 12 NC
Bài tập 14 trang 33 SGK Hình học 12 NC
Bài tập 15 trang 33 SGK Hình học 12 NC
Bài tập 16 trang 33 SGK Hình học 12 NC
Bài tập 17 trang 33 SGK Hình học 12 NC
Bài tập 18 trang 33 SGK Hình học 12 NC
Bài tập 19 trang 34 SGK Hình học 12 NC
Bài tập 20 trang 34 SGK Hình học 12 NC
Bài tập 21 trang 34 SGK Hình học 12 NC
Bài tập 22 trang 34 SGK Hình học 12 NC
Bài tập 23 trang 34 SGK Hình học 12 NC
Bài tập 24 trang 35 SGK Hình học 12 NC
Bài tập 25 trang 35 SGK Hình học 12 NC
Bài tập 26 trang 35 SGK Hình học 12 NC
Bài tập 27 trang 35 SGK Hình học 12 NC
Bài tập 28 trang 35 SGK Hình học 12 NC
Bài tập 29 trang 36 SGK Hình học 12 NC
Bài tập 30 trang 36 SGK Hình học 12 NC





