Giải bài 9 tr 26 sách GK Toán Hình lớp 12
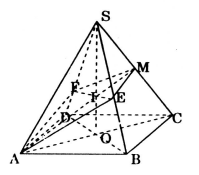
Cho hình chóp tứ giác đều S.ABCD đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc bằng 600. Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khối chóp S.AEMF.
Hướng dẫn giải chi tiết bài 9
Gọi O là giao điểm của AC và BD. AM cắt SO tại I.
Do mặt phẳng chứ AM, song song với BD nên E, F lần lượt là các giao điểm của đường thẳng qua I, song song với BD với các đường thẳng SB, SD.
Ta có: \(DB\perp AC\) (giả thiết)
\(SO\perp BD\) (vì S.ABCD là hình chóp đều)
Nên \(BD\perp (SAC)\Rightarrow EF\perp (SAC)\)
\(\Rightarrow EF\perp SC\) (1)
Mặt khác tam giác SAC cân tại S, hơn nữa theo giả thiết thì góc giữa SA và (ABCD) bằng 600 tức là góc \(\widehat{SAC}=60^0\) nên \(\Delta SAC\) đều. Vì M là trung điểm của SC nên \(AM\perp SC\) (2)
Từ (1) và (2), ta có: \(SC\perp (AEMF)\Rightarrow SM\) là chiều cao của khối chóp S.AEMF
Cũng từ \(EF\perp (SAC)\Rightarrow EF\perp AM\)
\(\Rightarrow S_{AEMF}=\frac{1}{2} EF.AM\)
\(\Rightarrow V_{S.AEMF}=\frac{1}{3}.\frac{1}{2}EF.AM.SM\) (*)
Vì \(\Delta SAC\) đều và \(AC=a\sqrt{2}\) (đường chéo của hình vuông cạnh a) nên \(SC=a\sqrt{2}\Rightarrow SM=\frac{a\sqrt{2}}{2}(3)\)
Cũng vì \(\Delta SAC\) đều cạnh \(a\sqrt{2}\) nên \(AM=\frac{a\sqrt{2}.\sqrt{3}}{2}=\frac{a\sqrt{6}}{2} \ (4)\)
Để thấy I là trọng tâm của tâm giác SDB nên theo định lý Talet ta có:
\(\frac{EF}{BD}=\frac{SI}{SO}=\frac{2}{3}\Rightarrow EF=\frac{2}{3}BD\)
\(= \frac{2}{3}a\sqrt{2} (5)\)
Thay (3), (4) và (5) vào (*) ta có:
\(V_{S.AEMF}=\frac{1}{6}.\frac{2}{3}.a\sqrt{2}.\frac{a\sqrt{2}}{2}. \frac{a\sqrt{6}}{2}=\frac{a^3\sqrt{6}}{18}\)
-- Mod Toán 12 HỌC247
-


Khẳng định nào sau đây sai về đa diện lồi?
bởi Bảo khanh
 07/06/2021
07/06/2021
A. Hình lập phương là đa diện lồi.
B. Tứ diện là đa diện lồi.
C. Hình hộp là đa diện lồi.
D. Hình tạo bởi hai khối lăng trụ có chung nhau một mặt bên là một hình đa diện lồi.
Theo dõi (0) 1 Trả lời -


Chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống khẳng định sau trở thành khẳng định đúng: “Số cạnh của một hình đa diện luôn … số đỉnh của hình đa diện ấy”.
bởi Mai Trang
 07/06/2021
07/06/2021
A. bằng
B. lớn hơn
C. nhỏ hơn
D. nhỏ hơn hoặc bằng
Theo dõi (0) 1 Trả lời -


Chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống khẳng định sau trở thành khẳng định đúng: “Số cạnh của một hình đa diện luôn … số mặt của hình đa diện ấy”.
bởi Việt Long
 07/06/2021
07/06/2021
A. bằng
B. nhỏ hơn hoặc bằng
C. nhỏ hơn
D. lớn hơn
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(ABCD\). Gọi \({h_A},{h_B},{h_C},{h_D}\;\) lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh: \(\dfrac{1}{{{h_A}}} + \dfrac{1}{{{h_B}}} + \dfrac{1}{{{h_C}}} + \dfrac{1}{{{h_D}}} = \dfrac{1}{r}\)
bởi Nguyễn Thị Lưu
 07/06/2021
07/06/2021
Cho tứ diện \(ABCD\). Gọi \({h_A},{h_B},{h_C},{h_D}\;\) lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh: \(\dfrac{1}{{{h_A}}} + \dfrac{1}{{{h_B}}} + \dfrac{1}{{{h_C}}} + \dfrac{1}{{{h_D}}} = \dfrac{1}{r}\)
Theo dõi (0) 1 Trả lời -


Hai đoạn thẳng \(AB\) và \(CD\) chéo nhau, \(AC\) là đường vuông góc chung của chúng. Biết rằng \(AC = h, AB = a, CD = b\) và góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({60^0}\). Hãy tính thể tích của khối tứ diện \(ABCD\).
bởi Bảo Hân
 07/06/2021
07/06/2021
Hai đoạn thẳng \(AB\) và \(CD\) chéo nhau, \(AC\) là đường vuông góc chung của chúng. Biết rằng \(AC = h, AB = a, CD = b\) và góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({60^0}\). Hãy tính thể tích của khối tứ diện \(ABCD\).
Theo dõi (0) 1 Trả lời -


Hãy tính thể tích khối lăng trụ có chiều cao bằng \(h\), đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính \(r\).
bởi Nguyen Ngoc
 07/06/2021
07/06/2021
Hãy tính thể tích khối lăng trụ có chiều cao bằng \(h\), đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính \(r\).
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác vuông cân ở \(C\). Cạnh \(B’B = a\) và tạo với đáy một góc bằng \({60^0}\). Hình chiếu vuông góc hạ từ \(B’\) lên đáy trùng với trọng tâm của tam giác \(ABC\). Hãy tính thể tích khối lăng trụ đó theo \(a\).
bởi Anh Tuyet
 06/06/2021
06/06/2021
Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác vuông cân ở \(C\). Cạnh \(B’B = a\) và tạo với đáy một góc bằng \({60^0}\). Hình chiếu vuông góc hạ từ \(B’\) lên đáy trùng với trọng tâm của tam giác \(ABC\). Hãy tính thể tích khối lăng trụ đó theo \(a\).
Theo dõi (0) 1 Trả lời -


Chứng minh mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
bởi Trịnh Lan Trinh
 06/06/2021
06/06/2021
Chứng minh mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Theo dõi (0) 1 Trả lời -


Hình được tạo thành từ hình lập phương \(ABCD.A’B’C’D’\) khi ta bỏ đi các điểm trong của mặt phẳng \( (ABCD) \) có phải là một hình đa diện không?
bởi Minh Thắng
 07/06/2021
07/06/2021
Hình được tạo thành từ hình lập phương \(ABCD.A’B’C’D’\) khi ta bỏ đi các điểm trong của mặt phẳng \( (ABCD) \) có phải là một hình đa diện không?
Theo dõi (0) 1 Trả lời -


Cho khối chóp \(S.ABC\) có thể tích bằng \(V\). Gọi \(B’\) và \(C’\) lần lượt là trung điểm của \(SB\) và \(SC\), \(A’\) nằm trên \(SA\) sao cho \(\overrightarrow {SA} = 3\overrightarrow {SA'} \). Tính thể tích khối chóp \(S.A’B’C’\) theo \(V\).
bởi Nguyễn Thủy Tiên
 07/06/2021
07/06/2021
Cho khối chóp \(S.ABC\) có thể tích bằng \(V\). Gọi \(B’\) và \(C’\) lần lượt là trung điểm của \(SB\) và \(SC\), \(A’\) nằm trên \(SA\) sao cho \(\overrightarrow {SA} = 3\overrightarrow {SA'} \). Tính thể tích khối chóp \(S.A’B’C’\) theo \(V\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 26 SGK Hình học 12
Bài tập 8 trang 26 SGK Hình học 12
Bài tập 10 trang 27 SGK Hình học 12
Bài tập 11 trang 27 SGK Hình học 12
Bài tập 12 trang 27 SGK Hình học 12
Bài tập 1 trang 27 SGK Hình học 12
Bài tập 2 trang 27 SGK Hình học 12
Bài tập 3 trang 27 SGK Hình học 12
Bài tập 4 trang 28 SGK Hình học 12
Bài tập 5 trang 28 SGK Hình học 12
Bài tập 6 trang 28 SGK Hình học 12
Bài tập 7 trang 28 SGK Hình học 12
Bài tập 8 trang 28 SGK Hình học 12
Bài tập 9 trang 28 SGK Hình học 12
Bài tập 10 trang 28 SGK Hình học 12
Bài tập 1.18 trang 19 SBT Hình học 12
Bài tập 1.19 trang 19 SBT Hình học 12
Bài tập 1.20 trang 19 SBT Hình học 12
Bài tập 1.21 trang 19 SBT Hình học 12
Bài tập 1.22 trang 19 SBT Hình học 12
Bài tập 1.23 trang 19 SBT Hình học 12
Bài tập 1.24 trang 19 SBT Hình học 12
Bài tập 1.25 trang 19 SBT Hình học 12
Bài tập 1.26 trang 19 SBT Hình học 12
Bài tập 1.27 trang 20 SBT Hình học 12
Bài tập 1.28 trang 20 SBT Hình học 12
Bài tập 1.29 trang 20 SBT Hình học 12
Bài tập 1.30 trang 20 SBT Hình học 12
Bài tập 1.31 trang 20 SBT Hình học 12
Bài tập 1.32 trang 20 SBT Hình học 12
Bài tập 1.33 trang 20 SBT Hình học 12
Bài tập 1.34 trang 20 SBT Hình học 12
Bài tập 1.35 trang 20 SBT Hình học 12
Bài tập 1.36 trang 21 SBT Hình học 12
Bài tập 1.37 trang 21 SBT Hình học 12
Bài tập 1.38 trang 21 SBT Hình học 12
Bài tập 1.39 trang 21 SBT Hình học 12
Bài tập 1.40 trang 21 SBT Hình học 12
Bài tập 1.41 trang 21 SBT Hình học 12
Bài tập 1.42 trang 21 SBT Hình học 12
Bài tập 1.43 trang 21 SBT Hình học 12
Bài tập 1.44 trang 22 SBT Hình học 12
Bài tập 1.45 trang 22 SBT Hình học 12
Bài tập 1.46 trang 22 SBT Hình học 12
Bài tập 1.47 trang 22 SBT Hình học 12
Bài tập 1.48 trang 22 SBT Hình học 12
Bài tập 1.49 trang 22 SBT Hình học 12
Bài tập 1.50 trang 22 SBT Hình học 12
Bài tập 1.51 trang 23 SBT Hình học 12
Bài tập 1.52 trang 23 SBT Hình học 12
Bài tập 1.53 trang 23 SBT Hình học 12
Bài tập 1.54 trang 23 SBT Hình học 12
Bài tập 1.55 trang 23 SBT Hình học 12
Bài tập 1.56 trang 23 SBT Hình học 12
Bài tập 1.57 trang 24 SBT Hình học 12
Bài tập 1.58 trang 24 SBT Hình học 12
Bài tập 1.59 trang 24 SBT Hình học 12
Bài tập 1 trang 30 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 31 SGK Hình học 12 NC
Bài tập 4 trang 31 SGK Hình học 12 NC
Bài tập 5 trang 31 SGK Hình học 12 NC
Bài tập 6 trang 31 SGK Hình học 12 NC
Bài tập 1 trang 31 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 32 SGK Hình học 12 NC
Bài tập 4 trang 32 SGK Hình học 12 NC
Bài tập 5 trang 32 SGK Hình học 12 NC
Bài tập 6 trang 32 SGK Hình học 12 NC
Bài tập 7 trang 32 SGK Hình học 12 NC
Bài tập 8 trang 32 SGK Hình học 12 NC
Bài tập 9 trang 32 SGK Hình học 12 NC
Bài tập 10 trang 32 SGK Hình học 12 NC
Bài tập 11 trang 33 SGK Hình học 12 NC
Bài tập 12 trang 33 SGK Hình học 12 NC
Bài tập 13 trang 33 SGK Hình học 12 NC
Bài tập 14 trang 33 SGK Hình học 12 NC
Bài tập 15 trang 33 SGK Hình học 12 NC
Bài tập 16 trang 33 SGK Hình học 12 NC
Bài tập 17 trang 33 SGK Hình học 12 NC
Bài tập 18 trang 33 SGK Hình học 12 NC
Bài tập 19 trang 34 SGK Hình học 12 NC
Bài tập 20 trang 34 SGK Hình học 12 NC
Bài tập 21 trang 34 SGK Hình học 12 NC
Bài tập 22 trang 34 SGK Hình học 12 NC
Bài tập 23 trang 34 SGK Hình học 12 NC
Bài tập 24 trang 35 SGK Hình học 12 NC
Bài tập 25 trang 35 SGK Hình học 12 NC
Bài tập 26 trang 35 SGK Hình học 12 NC
Bài tập 27 trang 35 SGK Hình học 12 NC
Bài tập 28 trang 35 SGK Hình học 12 NC
Bài tập 29 trang 36 SGK Hình học 12 NC
Bài tập 30 trang 36 SGK Hình học 12 NC