Giải bài 11 tr 27 sách GK Toán Hình lớp 12
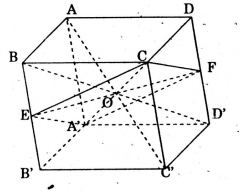
Cho hình hộp ABCD.A'B'C'D'. Gọi E và F theo thứ tự là trung điểm của các cạnh BB' và DD'. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số của hai khối đa diện đó.
Hướng dẫn giải chi tiết bài 11
Trước hết, ta xác định thiết diện của hình hộp ABCD.A'B'C'D' khi cắt bởi mp (CEF). Mặt phẳng (CEF) chứa đường thẳng EF mà E là trung điểm của BB', F là trung điểm của CC' nên EF chứa giao điểm O của các đường chéo hình hộp, do đó mặt phẳng (CEF) cùng chứa giao điểm O của các đường chéo và nó cũng chứa đường chéo A'C của hình hộp. Ta dễ dàng nhận xét rằng thiết diện chính là hình bình hành CEA'F. Qua EF ta dựng một mặt phẳng song song với đáy hình hộp, mặt phẳng này cắt AA' ở P và cắt CC' ở Q.
Ta có thể tích của hình hộp ABCD.PEQF là:
\(V_{ABCD.PEQF}=\frac{1}{2}V_{ABCD.A'B'C'D'}\) (1)
Ta cũng chứng minh được một cách dễ dàng:
\(V_{CFQE}=V_{AFPE}\) (2)
(Hai hình chóp CFQE và A'FPE có chiều cao bằng nhau và diện tích đáy bằng nhau)
Xét khối đa diện ABCDE'F do mặt phẳng (CEF) chia ra trên hình hộp ABCD.A'B'C'D', ta có:
\(V_{ABCD.FA'EQ}=V_{ABCD.FPE}+V_{A'FPE}\)
Từ (1), (2), (3) suy ra:
\(V_{ABCD.FA'EQ}=\frac{1}{2}.V_{ABCD.A'B'C'D'}\)
Vậy mặt phẳng (CEF) chia hình hộp thành hai khối đa diện có thể tích bằng nhau, tỉ số của chúng là 1.
Chú ý: Có thể lí luận như sau: Giao điểm O của các đường chéo của hình hộp là tâm đối xứng của hình hộp, do đó mặt phẳng (CEF) chứa điểm O nên chia hình hộp thành hai hình đối xứng với nhau qua điểm O. Vậy hai hình này là hai hình bằng nhau và có thể tích bằng nhau.
-- Mod Toán 12 HỌC247
-


Cho biết nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên n lần thì thể tích của nó tăng lên:
bởi Hoàng giang
 06/06/2021
06/06/2021
(A) \({n^2}\) lần
(B) \(2{n^2}\) lần
(C) \({n^3}\) lần
(D) \(2{n^3}\) lần
Theo dõi (0) 1 Trả lời -


Cho một khối chóp tam giác có cạnh đáy bằng \(6, 8, 10\). Một cạnh bên có độ dài bằng \(4\) và tạo với đáy góc \({60^0}\). Thể tích của khối chóp đó là:
bởi thanh duy
 06/06/2021
06/06/2021
(A) \(16\sqrt 3 \)
(B) \(8\sqrt 3 \)
(C) \(16{{\sqrt 2 } \over 3}\)
(D) \(16\pi \)
Theo dõi (0) 1 Trả lời -


Cho hình chóp tứ giác đều \(H\) có diện tích đáy bằng \(4\) và diện tích của một mặt bên bằng \(\sqrt 2 \). Tính thể tích của \(H\) là:
bởi trang lan
 06/06/2021
06/06/2021
(A) \({{4\sqrt 3 } \over 3}\)
(B) \(4\)
(C) \({4 \over 3}\)
(D) \({{4\sqrt 3 } \over 2}\)
Theo dõi (0) 1 Trả lời -


Cho một hình chóp tam giác đều có cạnh bên bằng \(b\) và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Thể tích của hình chóp là:
bởi Anh Linh
 07/06/2021
07/06/2021
(A) \({3 \over 4}{b^3}{\cos ^2}\alpha \sin \alpha \)
(B) \({{\sqrt 3 } \over 4}{b^3}{\cos ^2}\alpha \sin \alpha \)
(C) \({3 \over 4}{b^3}\cos \alpha {\sin ^2}\alpha \)
(D) \({{\sqrt 3 } \over 4}{b^3}\cos \alpha \sin \alpha \)
Theo dõi (0) 1 Trả lời -


Cho một hình chóp tam giác đều có cạnh đáy bằng \(a\) và cạnh bên tạo với mặt phẳng đáy một góc \(\alpha \). Hãy tính thể tích của hình chóp đó là:
bởi Thùy Nguyễn
 07/06/2021
07/06/2021
(A) \({{{a^3}\cot \alpha } \over {12}}\)
(B) \({{{a^3}tan\alpha } \over {12}}\)
(C) \({{{a^2}tan\alpha } \over {12}}\)
(D) \({{{a^3}tan\alpha } \over 4}\)
Theo dõi (0) 1 Trả lời -


Cho một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh \(12cm\) rồi gấp lại thành nột hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là \(4800\) \(c{m^3}\) thì cạnh tấm bìa đó có độ dài là:
bởi hồng trang
 07/06/2021
07/06/2021
(A) \(42cm\)
(B) \(36cm\)
(C) \(44cm\)
(D) \(38cm\)
Theo dõi (0) 1 Trả lời -


Cho biết đáy của một hình hộp là một hình thoi có cạnh bằng \(6cm\) và góc nhọn bằng \({45^0}\), cạnh bên của hình hộp dài \(10cm\) và tạo với mặt phẳng đáy một góc \({45^0}\). Khi đó thể tích của hình hộp là:
bởi Choco Choco
 06/06/2021
06/06/2021
(A) \(124\sqrt 3 \,\,c{m^3}\)
(B) \(180\,\,c{m^3}\)
(C) \(120\sqrt 2 \,\,c{m^3}\)
(D) \(180\sqrt 2 \,\,c{m^3}\)
Theo dõi (0) 1 Trả lời -


Cho một khối lăng trụ tam giác có các cạnh đáy bằng \(19, 20, 37\), chiều cao của khối lăng trụ bằng trung bình cộng của các cạnh đáy. Khi đó thể tích của khối lăng trụ là:
bởi Dương Quá
 06/06/2021
06/06/2021
(A) \(2888\)
(B) \(1245\sqrt 2 \)
(C) \(1123\)
(D) \(4273\)
Theo dõi (0) 1 Trả lời -


Cho khối \(12\) mặt đều \((H)\) có thể tích \(V\) và diện tích mỗi mặt của nó bằng S. Cho biết tổng các khoảng cách từ một điểm nằm trong \((H)\) đến các mặt của nó bằng:
bởi Phong Vu
 06/06/2021
06/06/2021
(A) \({{3V} \over {4S}}\)
(B) \({V \over {4S}}\)
(C) \({{3V} \over S}\)
(D) \({V \over {12S}}\)
Theo dõi (0) 1 Trả lời -


Với khối tứ diện đều có cạnh bằng \(a\). Khi đó, thể tích của khối tám mặt đều mà các đỉnh là trung điểm của các cạnh của khối tứ diện đã cho là:
bởi Thuy Kim
 06/06/2021
06/06/2021
(A) \({{{a^3}\sqrt 2 } \over {24}}\)
(B) \({{{a^3}\sqrt 3 } \over {12}}\)
(C) \({{{a^3}\sqrt 2 } \over 6}\)
(D) \({{{a^3}\sqrt 3 } \over {24}}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 9 trang 26 SGK Hình học 12
Bài tập 10 trang 27 SGK Hình học 12
Bài tập 12 trang 27 SGK Hình học 12
Bài tập 1 trang 27 SGK Hình học 12
Bài tập 2 trang 27 SGK Hình học 12
Bài tập 3 trang 27 SGK Hình học 12
Bài tập 4 trang 28 SGK Hình học 12
Bài tập 5 trang 28 SGK Hình học 12
Bài tập 6 trang 28 SGK Hình học 12
Bài tập 7 trang 28 SGK Hình học 12
Bài tập 8 trang 28 SGK Hình học 12
Bài tập 9 trang 28 SGK Hình học 12
Bài tập 10 trang 28 SGK Hình học 12
Bài tập 1.18 trang 19 SBT Hình học 12
Bài tập 1.19 trang 19 SBT Hình học 12
Bài tập 1.20 trang 19 SBT Hình học 12
Bài tập 1.21 trang 19 SBT Hình học 12
Bài tập 1.22 trang 19 SBT Hình học 12
Bài tập 1.23 trang 19 SBT Hình học 12
Bài tập 1.24 trang 19 SBT Hình học 12
Bài tập 1.25 trang 19 SBT Hình học 12
Bài tập 1.26 trang 19 SBT Hình học 12
Bài tập 1.27 trang 20 SBT Hình học 12
Bài tập 1.28 trang 20 SBT Hình học 12
Bài tập 1.29 trang 20 SBT Hình học 12
Bài tập 1.30 trang 20 SBT Hình học 12
Bài tập 1.31 trang 20 SBT Hình học 12
Bài tập 1.32 trang 20 SBT Hình học 12
Bài tập 1.33 trang 20 SBT Hình học 12
Bài tập 1.34 trang 20 SBT Hình học 12
Bài tập 1.35 trang 20 SBT Hình học 12
Bài tập 1.36 trang 21 SBT Hình học 12
Bài tập 1.37 trang 21 SBT Hình học 12
Bài tập 1.38 trang 21 SBT Hình học 12
Bài tập 1.39 trang 21 SBT Hình học 12
Bài tập 1.40 trang 21 SBT Hình học 12
Bài tập 1.41 trang 21 SBT Hình học 12
Bài tập 1.42 trang 21 SBT Hình học 12
Bài tập 1.43 trang 21 SBT Hình học 12
Bài tập 1.44 trang 22 SBT Hình học 12
Bài tập 1.45 trang 22 SBT Hình học 12
Bài tập 1.46 trang 22 SBT Hình học 12
Bài tập 1.47 trang 22 SBT Hình học 12
Bài tập 1.48 trang 22 SBT Hình học 12
Bài tập 1.49 trang 22 SBT Hình học 12
Bài tập 1.50 trang 22 SBT Hình học 12
Bài tập 1.51 trang 23 SBT Hình học 12
Bài tập 1.52 trang 23 SBT Hình học 12
Bài tập 1.53 trang 23 SBT Hình học 12
Bài tập 1.54 trang 23 SBT Hình học 12
Bài tập 1.55 trang 23 SBT Hình học 12
Bài tập 1.56 trang 23 SBT Hình học 12
Bài tập 1.57 trang 24 SBT Hình học 12
Bài tập 1.58 trang 24 SBT Hình học 12
Bài tập 1.59 trang 24 SBT Hình học 12
Bài tập 1 trang 30 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 31 SGK Hình học 12 NC
Bài tập 4 trang 31 SGK Hình học 12 NC
Bài tập 5 trang 31 SGK Hình học 12 NC
Bài tập 6 trang 31 SGK Hình học 12 NC
Bài tập 1 trang 31 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 32 SGK Hình học 12 NC
Bài tập 4 trang 32 SGK Hình học 12 NC
Bài tập 5 trang 32 SGK Hình học 12 NC
Bài tập 6 trang 32 SGK Hình học 12 NC
Bài tập 7 trang 32 SGK Hình học 12 NC
Bài tập 8 trang 32 SGK Hình học 12 NC
Bài tập 9 trang 32 SGK Hình học 12 NC
Bài tập 10 trang 32 SGK Hình học 12 NC
Bài tập 11 trang 33 SGK Hình học 12 NC
Bài tập 12 trang 33 SGK Hình học 12 NC
Bài tập 13 trang 33 SGK Hình học 12 NC
Bài tập 14 trang 33 SGK Hình học 12 NC
Bài tập 15 trang 33 SGK Hình học 12 NC
Bài tập 16 trang 33 SGK Hình học 12 NC
Bài tập 17 trang 33 SGK Hình học 12 NC
Bài tập 18 trang 33 SGK Hình học 12 NC
Bài tập 19 trang 34 SGK Hình học 12 NC
Bài tập 20 trang 34 SGK Hình học 12 NC
Bài tập 21 trang 34 SGK Hình học 12 NC
Bài tập 22 trang 34 SGK Hình học 12 NC
Bài tập 23 trang 34 SGK Hình học 12 NC
Bài tập 24 trang 35 SGK Hình học 12 NC
Bài tập 25 trang 35 SGK Hình học 12 NC
Bài tập 26 trang 35 SGK Hình học 12 NC
Bài tập 27 trang 35 SGK Hình học 12 NC
Bài tập 28 trang 35 SGK Hình học 12 NC
Bài tập 29 trang 36 SGK Hình học 12 NC
Bài tập 30 trang 36 SGK Hình học 12 NC