Giải bài 8 tr 26 sách GK Toán Hình lớp 12
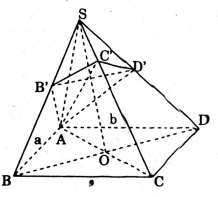
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. SA vuông góc với đáy và AB=a, AD=b, SA=c. Lấy các điểm B', D' theo thứ tự thuộc SB, SD sao cho \(AB'\perp SB, AD'\perp SD\). Mặt phẳng (AB'D') cắt SC tại C'. Tính thể tích khối chóp S.AB'C'D'.
Hướng dẫn giải chi tiết bài 8
Dựng điểm C' như hình vẽ.
Ta có: \(BC\perp AB\) (giả thiết) (1)
Mặt khác: \(SA\perp (ABCD)\) nên \(SA\perp BC\) (2)
Từ (1) và (2) ta có: \(BC\perp (SAB)\)
\(\Rightarrow BC\perp AB'\) (3)
Ta có: \(AB'\perp SB\) (giả thiết) (4)
Từ (3) và (4) suy ra suy ra \(AB'\perp (SBC)\)
Hay ta có được \(AB'\perp BC'\)
\(\Leftrightarrow \Delta AB'C'\) vuông tại B'
Hoàn toàn tương tự ta cũng có \(\Delta AD'C'\) vuông tại D'
Ta có: \(AB'\perp SC;AD'\perp SC\)
(vì \(AB'\perp (SBC), AD'\perp (SDC)\))
Nên \(SC\perp (AB'C'D')\). Vì vậy:
\(V_{S.AB'C'D'}=\frac{1}{3}.S_{AB'C'D'}.SC'\)
\(=\frac{1}{3} \left [ S_{\Delta AB'C'}+S_{\Delta AD'C'} \right ].SC'\)
\(=\frac{1}{6}\left [ AB'.B'C'+AD'.D'C' \right ].SC' \ \ (*)\)
Ta có:
\(\frac{1}{AB^2}=\frac{1}{a^2}+\frac{1}{c^2}=\frac{a^2+c^2}{a^2.c^2} \)
\(\Rightarrow AB^2=\frac{a^2.c^2}{a^2+c^2}\Rightarrow AB^2= \frac{ac}{\sqrt{a^2+c^2}}\) (5)
Tương tự: \(AD'^2=\frac{b^2c^2}{b^2+c^2}\Rightarrow AD'=\frac{bc}{\sqrt{b^2+c^2}}\) (6)
\(\frac{1}{AC'^2}=\frac{1}{c^2}+\frac{1}{AC^2}=\frac{1}{c^2}+\frac{1}{a^2+b^2}\)
\(= \frac{a^2+b^2+c^2}{c^2(a^2+b^2)}\)
\(\Rightarrow AC'^2=\frac{c^2(a^2+b^2)}{a^2+b^2+c^2}\)
\(\Rightarrow AC'= \frac{c\sqrt{a^2+b^2}}{\sqrt{a^2+b^2+c^2}}\) (7)
\(\Rightarrow B'C'^2=AC'^2-AB'^2\)
\(=-\frac{a^2c^2}{a^2+c^2}+\frac{c^2(a^2+b^2)}{a^2+b^2+c^2}\)
\(=\frac{-a^4c^2-a^2b^2c^2-a^2c^4+a^4c^2+c^4a^2+a^2b^2c^2+c^4b^2} {(a^2+c^2)(a^2+b^2+c^2)}\)
\(=\frac{c^4b^2}{(a^2+c^2)(a^2+b^2+c^2)}\)
\(\Rightarrow B'C'=\frac{c^2b}{\sqrt{(a^2+c^2)(a^2+b^2+c^2)}} \ \ (8)\)
Tương tự: \(C'D'=\frac{c^2a}{\sqrt{(b^2+c^2)(a^2+b^2+c^2)}} \ \ (9);\)
\(SC'= \frac{c^2}{\sqrt{a^2+b^2+c^2}} \ \ (10)\)
Thay (5) (6) (7) (8) (9) và (10) vào (*) ta có:
\(V_{S.AB'C'D'}=\)
\(\frac{1}{6}\Bigg [ \frac{ac}{\sqrt{a^2+c^2}}.\frac{c^2b}{(a^2+c^2)(a^2+b^2+c^2)}\).\(+ \frac{bc}{\sqrt{a^2+c^2}}. \frac{c^2a}{\sqrt{(b^2+c^2)}(a^2+b^2+c^2)} \Bigg ]\) \(\frac{c^2}{\sqrt{a^2+b^2+c^2}}\)
\(=\frac{1}{6}\frac{c^5ab}{a^2+b^2+c^2} \left [ \frac{1}{a^2+c^2}+\frac{1}{b^2+c^2} \right ]\)
-- Mod Toán 12 HỌC247
-


Cho tứ diện \(ABCD\). Gọi \(B'\) và \(C'\) lần lượt là trung điểm của \(AB\) và \(AC\). Tỉ số thể tích của khối tứ diện \(AB'C'D\) và khối tứ diện \(ABCD\) bằng bao nhiêu?
bởi Tram Anh
 07/06/2021
07/06/2021
A. \(\dfrac{1}{2}\)
B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{6}\)
D. \(\dfrac{1}{8}\)
Theo dõi (0) 1 Trả lời -


Cho \(\left( H \right)\) là khối chóp tứ giác đều có tất cả các cạnh bằng \(a\). Hãy tính thể tích của \(\left( H \right)\) là:
bởi Mai Linh
 07/06/2021
07/06/2021
A. \(\dfrac{{{a^3}}}{3}\)
B. \(\dfrac{{{a^3}\sqrt 2 }}{6}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
D. \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
Theo dõi (0) 1 Trả lời -


Với \(\left( H \right)\) là khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng \(a\). Thể tích của \(\left( H \right)\) bằng:
bởi Nguyễn Hiền
 06/06/2021
06/06/2021
A. \(\dfrac{{{a^3}}}{2}\)
B. \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
D. \(\dfrac{{{a^3}\sqrt 3 }}{3}\)
Theo dõi (0) 1 Trả lời -


Số đỉnh của hình hai mươi mặt đều là bao nhiêu?
bởi Mai Vàng
 07/06/2021
07/06/2021
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi
Theo dõi (0) 1 Trả lời -


Số cạnh của hình mười hai mặt đều là bằng?
bởi Lê Trung Phuong
 06/06/2021
06/06/2021
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi
Theo dõi (0) 1 Trả lời -


Hãy cho biết số đỉnh của hình mười hai mặt đều là:
bởi na na
 07/06/2021
07/06/2021
A. Mười hai
B. Mười sáu
C. Hai mươi
D. Ba mươi
Theo dõi (0) 1 Trả lời -


Cho biết số đỉnh của hình bát diện đều là bằng:
bởi Hữu Trí
 07/06/2021
07/06/2021
A. Sáu
B. Tám
C. Mười
D. Mười hai
Theo dõi (0) 1 Trả lời -


Số cạnh của hình bát diện đều là bằng bao nhiêu?
bởi sap sua
 07/06/2021
07/06/2021
A. Tám
B. Mười
C. Mười hai
D. Mười sáu
Theo dõi (0) 1 Trả lời -


A. Hai
B. Vô số
C. Bốn
D. Sáu
Theo dõi (0) 1 Trả lời -


A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
D. Mỗi mặt có ít nhất ba cạnh.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 6 trang 26 SGK Hình học 12
Bài tập 7 trang 26 SGK Hình học 12
Bài tập 9 trang 26 SGK Hình học 12
Bài tập 10 trang 27 SGK Hình học 12
Bài tập 11 trang 27 SGK Hình học 12
Bài tập 12 trang 27 SGK Hình học 12
Bài tập 1 trang 27 SGK Hình học 12
Bài tập 2 trang 27 SGK Hình học 12
Bài tập 3 trang 27 SGK Hình học 12
Bài tập 4 trang 28 SGK Hình học 12
Bài tập 5 trang 28 SGK Hình học 12
Bài tập 6 trang 28 SGK Hình học 12
Bài tập 7 trang 28 SGK Hình học 12
Bài tập 8 trang 28 SGK Hình học 12
Bài tập 9 trang 28 SGK Hình học 12
Bài tập 10 trang 28 SGK Hình học 12
Bài tập 1.18 trang 19 SBT Hình học 12
Bài tập 1.19 trang 19 SBT Hình học 12
Bài tập 1.20 trang 19 SBT Hình học 12
Bài tập 1.21 trang 19 SBT Hình học 12
Bài tập 1.22 trang 19 SBT Hình học 12
Bài tập 1.23 trang 19 SBT Hình học 12
Bài tập 1.24 trang 19 SBT Hình học 12
Bài tập 1.25 trang 19 SBT Hình học 12
Bài tập 1.26 trang 19 SBT Hình học 12
Bài tập 1.27 trang 20 SBT Hình học 12
Bài tập 1.28 trang 20 SBT Hình học 12
Bài tập 1.29 trang 20 SBT Hình học 12
Bài tập 1.30 trang 20 SBT Hình học 12
Bài tập 1.31 trang 20 SBT Hình học 12
Bài tập 1.32 trang 20 SBT Hình học 12
Bài tập 1.33 trang 20 SBT Hình học 12
Bài tập 1.34 trang 20 SBT Hình học 12
Bài tập 1.35 trang 20 SBT Hình học 12
Bài tập 1.36 trang 21 SBT Hình học 12
Bài tập 1.37 trang 21 SBT Hình học 12
Bài tập 1.38 trang 21 SBT Hình học 12
Bài tập 1.39 trang 21 SBT Hình học 12
Bài tập 1.40 trang 21 SBT Hình học 12
Bài tập 1.41 trang 21 SBT Hình học 12
Bài tập 1.42 trang 21 SBT Hình học 12
Bài tập 1.43 trang 21 SBT Hình học 12
Bài tập 1.44 trang 22 SBT Hình học 12
Bài tập 1.45 trang 22 SBT Hình học 12
Bài tập 1.46 trang 22 SBT Hình học 12
Bài tập 1.47 trang 22 SBT Hình học 12
Bài tập 1.48 trang 22 SBT Hình học 12
Bài tập 1.49 trang 22 SBT Hình học 12
Bài tập 1.50 trang 22 SBT Hình học 12
Bài tập 1.51 trang 23 SBT Hình học 12
Bài tập 1.52 trang 23 SBT Hình học 12
Bài tập 1.53 trang 23 SBT Hình học 12
Bài tập 1.54 trang 23 SBT Hình học 12
Bài tập 1.55 trang 23 SBT Hình học 12
Bài tập 1.56 trang 23 SBT Hình học 12
Bài tập 1.57 trang 24 SBT Hình học 12
Bài tập 1.58 trang 24 SBT Hình học 12
Bài tập 1.59 trang 24 SBT Hình học 12
Bài tập 1 trang 30 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 31 SGK Hình học 12 NC
Bài tập 4 trang 31 SGK Hình học 12 NC
Bài tập 5 trang 31 SGK Hình học 12 NC
Bài tập 6 trang 31 SGK Hình học 12 NC
Bài tập 1 trang 31 SGK Hình học 12 NC
Bài tập 2 trang 31 SGK Hình học 12 NC
Bài tập 3 trang 32 SGK Hình học 12 NC
Bài tập 4 trang 32 SGK Hình học 12 NC
Bài tập 5 trang 32 SGK Hình học 12 NC
Bài tập 6 trang 32 SGK Hình học 12 NC
Bài tập 7 trang 32 SGK Hình học 12 NC
Bài tập 8 trang 32 SGK Hình học 12 NC
Bài tập 9 trang 32 SGK Hình học 12 NC
Bài tập 10 trang 32 SGK Hình học 12 NC
Bài tập 11 trang 33 SGK Hình học 12 NC
Bài tập 12 trang 33 SGK Hình học 12 NC
Bài tập 13 trang 33 SGK Hình học 12 NC
Bài tập 14 trang 33 SGK Hình học 12 NC
Bài tập 15 trang 33 SGK Hình học 12 NC
Bài tập 16 trang 33 SGK Hình học 12 NC
Bài tập 17 trang 33 SGK Hình học 12 NC
Bài tập 18 trang 33 SGK Hình học 12 NC
Bài tập 19 trang 34 SGK Hình học 12 NC
Bài tập 20 trang 34 SGK Hình học 12 NC
Bài tập 21 trang 34 SGK Hình học 12 NC
Bài tập 22 trang 34 SGK Hình học 12 NC
Bài tập 23 trang 34 SGK Hình học 12 NC
Bài tập 24 trang 35 SGK Hình học 12 NC
Bài tập 25 trang 35 SGK Hình học 12 NC
Bài tập 26 trang 35 SGK Hình học 12 NC
Bài tập 27 trang 35 SGK Hình học 12 NC
Bài tập 28 trang 35 SGK Hình học 12 NC
Bài tập 29 trang 36 SGK Hình học 12 NC
Bài tập 30 trang 36 SGK Hình học 12 NC