Bài tập 10 trang 27 SGK Hình học 12

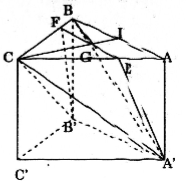
Câu a:

Ta tính thể tích hình chóp A'.BCB'.

Gọi M là trung điểm của B'C', ta có: \(A'M\perp B'C'\)  (1)

Lăng trụ ABC.A'B'C' là lăng trụ đứng nên: \(BB'\perp (A'B'C')\)

\(\Rightarrow BB'\perp A'M\)

Từ (1) và (2) suy ra \(A'M\perp (BB'C)\) hay A'M là đường cao của hình chóp A'.BCB'.

Ta có: \(A'M=\frac{a\sqrt{3}}{2};S_{BB'C}=\frac{1}{2}a^2\)

\(\Rightarrow V_{A'BB'C}=\frac{1}{3}A'M.S_{BB'C}\)

\(\Rightarrow V_{A'BB'C}=\frac{a^3\sqrt{3}}{12}\)

Câu b:

Thể tích hình chóp C.A'B'EF bằng tổng thể tích hai hình chóp:

- V₁ là thể tích hình chóp đỉnh B', đáy là tam giác CEF.

- V₂ là thể tích hình chóp đỉnh B', đáy là tam giác A'EC.

Do mp (ABC) // mp(A'B'C') nên dễ thấy EF // AB. Ta cũng có: \(EF=\frac{2}{3}a\)

Hình chóp B'.CEF có chiều cao BB' = a và diện tích đáy là:

\(S_{CEF}=\frac{1}{2}.\frac{2a}{3}.\frac{2}{3}.\frac{a\sqrt{3}}{3}=\frac{a^2\sqrt{3}}{9}\)

Từ đây ta có: \(V_1=\frac{a^3\sqrt{3}}{27}\)

Do \(EC=\frac{2}{3}AC\) nên:

\(S_{A'EC}=\frac{2}{3}a.\frac{1}{2}a=\frac{a^2}{3}\)

Hình chóp B'.A'EC có chiều cao là B'I (chiều cao của \(\Delta A'B'C'\)) bằng \(\frac{a\sqrt{3}}{2}\) nên \(V_2=\frac{a^3\sqrt{3}}{18}\)

Vậy thể tích hình chóp C.A'B'FE là: \(V=V_1+V_2=\frac{5a^3\sqrt{3}}{54}\)

-- Mod Toán 12 HỌC247