Toán 11 Ôn tập chương 2 Đường thẳng và mặt phẳng trong không gian

Tóm tắt lý thuyết

1.1. Đường thẳng và mặt phẳng song song

a) Định nghĩa:

Đường thẳng và mặt phẳng gọi là song song với nhau nếu chúng không có điểm nào chung.

\(a//(P) \Leftrightarrow a \cap (P) = \emptyset \)

Đường thẳng và mặt phẳng song song

b) Các định lý:

ĐL1:Nếu đường thẳng d không nằm trên mp(P) và song song với đường thẳng a nằm trên mp(P) thì đường thẳng d song song với mp(P)	\(\left\{ \begin{array}{l}d \not\subset (P)\\d//a\\a \subset (P)\end{array} \right. \Rightarrow d//(P)\)
ĐL2: Nếu đường thẳng a song song với mp(P) thì mọi mp(Q) chứa a mà cắt mp(P) thì cắt theo giao tuyến song song với a.	\(\left\{ \begin{array}{l}a//(P)\\a \subset (Q)\\(P) \cap (Q) = d\end{array} \right. \Rightarrow d//a\)
ĐL3: Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó.	\(\left\{ \begin{array}{l}(P) \cap (Q) = d\\(P)//a\\(Q)//a\end{array} \right. \Rightarrow d//a\)

1.2. Hai mặt phẳng song song

a) Định nghĩa:

Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm nào chung.

\((P)//(Q) \Leftrightarrow (P) \cap (Q) = \emptyset \)

Hai mặt phẳng song song

b) Các định lý:

ĐL1: Nếu mp(P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.	\(\left\{ \begin{array}{l}a,b \subset (P)\\a \cap b = I\\a//(Q),b//(Q)\end{array} \right. \Rightarrow (P)//(Q)\)
ĐL2: Nếu một đường thẳng nằm một trong hai mặt phẳng song song thì song song với mặt phẳng kia.	\(\left\{ \begin{array}{l}(P)//(Q)\\a \subset (P)\end{array} \right. \Rightarrow a//(Q)\)
ĐL3: Nếu hai mặt phẳng (P) và (Q) song song thì mọi mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.	\(\left\{ \begin{array}{l}(P)//(Q)\\(R) \cap (P) = a\\(R) \cap (Q) = b\end{array} \right. \Rightarrow a//b\)

Bài tập minh họa

Bài 1:

Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên đoạn \(BD\) lấy điểm \(P\) sao cho \(BP = 3PD\).

a) Tìm giao điểm của đường thẳng \(CD\) với mặt phẳng \(\left( {MNP} \right)\).

b) Tìm giao tuyến của hai mặt phẳng \(\left( {ABD} \right)\) và \(\left( {MNP} \right)\).

Hướng dẫn:

a) Trong \(\left( {BCD} \right)\) gọi \(E = CD \cap NP\) thì

\(\left\{ \begin{array}{l}E \in CD\\E \in NP \subset \left( {MNP} \right)\end{array} \right.\)

\( \Rightarrow E = CD \cap \left( {MNP} \right)\).

b) Trong \(\left( {ACD} \right)\) gọi \(Q = AD \cap ME\) thì ta có\(\left( {MNP} \right) \cap \left( {ABD} \right) = PQ\)

Bài 2:

Cho tứ diện \(ABCD\). Gọi \(I,J\) lần lượt là trung điểm của \(BC\) và \(BD\), \(E\) là một điểm thuộc cạnh \(AD\)( \(E\) khác \(A\) và \(D\)).

a) Xác định thiết diện của tứ diện với \(\left( {IJE} \right)\).

b) Tìm vị trí của điểm \(E\) trên \(AD\) sao cho thiết diện là hình bình hành.

c) Tìm điều kiện của tứ diện \(ABCD\) và vị trí của điểm \(E\) trên \(AD\) sao cho thiết diện là hình thoi.

Hướng dẫn:

a) Ta có \(\left\{ \begin{array}{l}F \in \left( {IJF} \right) \cap \left( {ACD} \right)\\IJ \subset \left( {IJF} \right),CD \subset \left( {ACD} \right)\\IJ\parallel CD\end{array} \right. \Rightarrow \left( {IJF} \right) \cap \left( {ACD} \right) = FE\parallel CD\parallel IJ\).

Thiết diện là tứ giác \(IJEF\).

b) Để thiết diện \(IJEF\) là hình bình hành thì \(IJ\parallel = EF\) mà \(IJ\parallel = \frac{1}{2}CD\) nên \(EF\parallel = \frac{1}{2}CD\), hay \(EF\) là đường trung bình trong tam giác \(ACD\)ứng với cạnh \(CD\) do đó \(E\) là trung điểm của \(AD\).

c) Để thiết diện \(IJEF\) là hình thoi thì trước tiên nó phải là hình bình hành, khi đó \(E\) là trung điểm của \(AD\). Mặt khác \(IJEF\) là hình thoi thì \(IJ = IF\), mà \(IJ = \frac{1}{2}CD,IF = \frac{1}{2}AB \Rightarrow AB = CD\).

Vậy điều kiện để thiết diện là hình thoi là tứ diện \(ABCD\) có \(AB = CD\) và \(E\) là trung điểm của \(AD\).

Bài 3:

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,P\) lần lượt là trung điểm các cạnh \(AB,CD,SA\).

a) Chứng minh \(\left( {SBN} \right)\parallel \left( {DPM} \right)\).

b) \(Q\) là một điểm thuộc đoạn \(SP\)(\(Q\) khác \(S,P\)). Xác định thiết diện của hình chóp cắt bởi \(\left( \alpha \right)\) đi qua \(Q\) và song song với \(\left( {SBN} \right)\).

c) Xác định thiết diện của hình chóp cắt bởi \(\left( \beta \right)\) đi qua \(MN\) song song với \(\left( {SAD} \right)\).

Hướng dẫn:

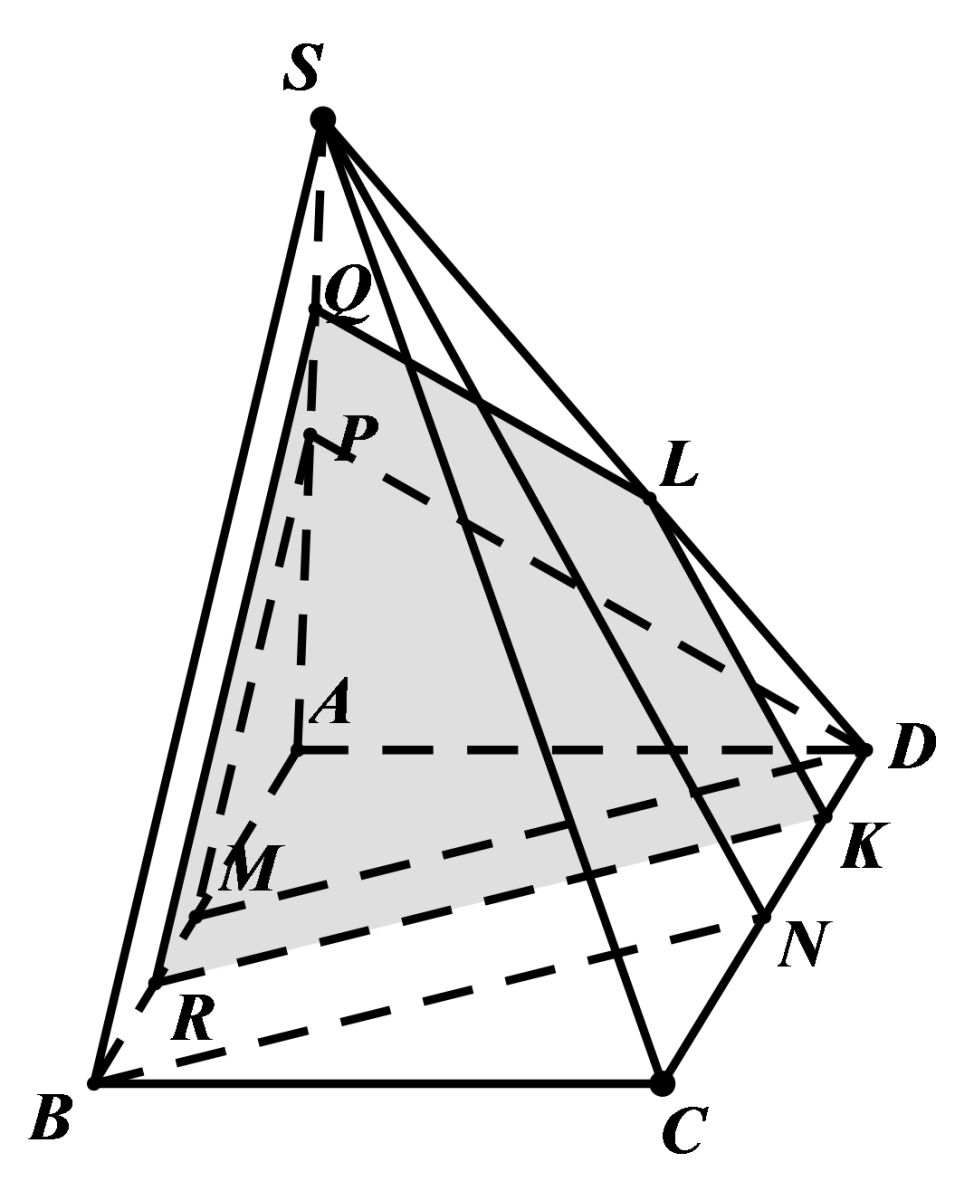
a) Ta có \(\left\{ \begin{array}{l}BN\parallel DM\\DM \subset \left( {DPM} \right)\end{array} \right. \Rightarrow BN\parallel \left( {DPM} \right){\rm{ }}\left( 1 \right)\)Tương tự \(\left\{ \begin{array}{l}BS\parallel MP\\MP \subset \left( {DPM} \right)\end{array} \right. \Rightarrow BS\parallel \left( {DPM} \right){\rm{ }}\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\left( {SBN} \right)\parallel \left( {DPM} \right)\).

b) Ta có \(\left\{ \begin{array}{l}SB \subset \left( {SBN} \right)\\\left( \alpha \right)\parallel \left( {SBN} \right)\end{array} \right. \Rightarrow SB\parallel \left( \alpha \right)\).

vậy\(\left\{ \begin{array}{l}Q \in \left( {SAB} \right) \cap \left( \alpha \right)\\SB \subset \left( {SAB} \right)\\SB\parallel \left( \alpha \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = QR\parallel SB,R \in AB\) .

Tương tự

\(\left( \alpha \right) \cap \left( {ABCD} \right) = RK\parallel BN,K \in CD\)

\(\left( \alpha \right) \cap \left( {SCD} \right) = KL\parallel SB,L \in SD\).

Vậy thiết diện là tứ giác \(QRKL\).

c)

Ta có \(\begin{array}{l}\left\{ \begin{array}{l}M \in \left( \beta \right) \cap \left( {SAB} \right)\\SA\parallel \left( \beta \right)\\SA \subset \left( {SAB} \right)\end{array} \right.\\ \Rightarrow \left( \beta \right) \cap \left( {SAB} \right) = MF\parallel SA,F \in SB\end{array}\)

Tương tự \(\left( \beta \right) \cap \left( {SCD} \right) = NE//SD,E \in SC\).

Thiết diện là hình thang \(MNEF\).

3. Luyện tập Bài 6 chương 2 hình học 11

Bài ôn tập chương Đường thẳng và mặt phẳng trong không gian - Quan hệ song song sẽ giúp các em hệ thống lại toàn bộ kiến thức đã học ở chương II Hình học 11. Thông qua phần tóm tắt kiến thưc trọng tâm, các em sẽ có được cách ghi nhớ bài một cách dễ dàng, hiệu quả.

3.1 Trắc nghiệm về Ôn tập đường thẳng và mặt phẳng trong không gian - Quan hệ song song

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Ôn tập chương II để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Trong các khẳng định sau, khẳng định nào đúng?
- A. Hai đường thẳng chéo nhau thì chúng có điểm chung.
- B. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
- C. Hai đường thẳng song song với nhau khi chúng ở trên cùng một mặt phẳng.
- D. Khi hai đường thẳng ở trên hai mặt phẳng phân biệt thì hai đường thẳng đó chéo nhau.
Câu 2:
Cho hai đường thẳng chéo nhau \(a,\;b\) và điểm \(M\) ở ngoài \(a\) và ngoài \(b\). Có nhiều nhất bao nhiêu đường thẳng qua \(M\) cắt cả \(a\) và \(b\)?
- A. 1
- B. 2
- C. 0
- D. Vô số
Câu 3:
Cho hình chóp \(S.ABCD\) có \(AD\) không song song với \(BC.\) Gọi \(M,N,\) \(P,Q,R,T\)lần lượt là trung điểm \(AC,BD,BC,CD,SA,SD.\) Cặp đường thẳng nào sau đây song song với nhau?
- A. \(MP\) và \(RT.\)
- B. \(MQ\) và \(RT.\)
- C. \(MN\) và \(RT.\)
- D. \(PQ\) và \(RT.\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK và Nâng Cao về Ôn tập đường thẳng và mặt phẳng trong không gian - Quan hệ song song

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Ôn tập chương II sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.

Bài tập 1 trang 77 SGK Hình học 11

Bài tập 2 trang 77 SGK Hình học 11

Bài tập 3 trang 77 SGK Hình học 11

Bài tập 4 trang 77 SGK Hình học 11

Bài tập 5 trang 77 SGK Hình học 11

Bài tập 6 trang 77 SGK Hình học 11

Bài tập 7 trang 77 SGK Hình học 11

Bài tập 1 trang 77 SGK Hình học 11

Bài tập 2 trang 77 SGK Hình học 11

Bài tập 3 trang 77 SGK Hình học 11

Bài tập 4 trang 78 SGK Hình học 11

Bài tập 1 trang 78 SGK Hình học 11