Giải bài 2.42 tr 82 SBT Hình học 11
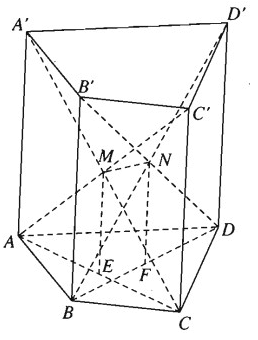
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'.
a) Chứng minh rằng hai đường chéo AC' và A'C cắt nhau và hai đường chéo BD' và B'D cắt nhau.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.
Hướng dẫn giải chi tiết
a) Hình bình hành ACC’A có hai đường chéo là AC’ và A’C, cắt nhau tại trung điểm M của mỗi đường. Tương tự, hai đường chéo BD’ và B’D cắt nhau tại trung điểm N của mỗi đường.
b) Trung điểm E của AC là hình chiếu của trung điểm M của AC’ thep phương của cạnh lăng trụ. Tương tự, trung điểm F là hình chiếu trung điểm N của đường chéo BD’ trên BD. Ta có EM //CC′ và \(EM = \frac{{CC'}}{2}\).
Mặt khác FN // DD′ và \(FN = \frac{{DD'}}{2}\). Từ đó suy ra tứ giác MNFE là hình bình hành và ta có MN = EF.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 2.40 trang 81 SBT Hình học 11
Bài tập 2.41 trang 82 SBT Hình học 11
Bài tập 2.43 trang 82 SBT Hình học 11
Bài tập 2.44 trang 82 SBT Hình học 11
Bài tập 2.45 trang 83 SBT Hình học 11
Bài tập 2.46 trang 83 SBT Hình học 11
Bài tập 2.47 trang 83 SBT Hình học 11
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.50 trang 84 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC