Giải bài 2.41 tr 82 SBT Hình học 11
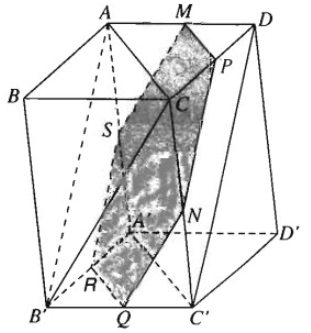
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnhAD và CC’ sao cho \(\frac{{AM}}{{MD}} = \frac{{CN}}{{NC'}}\)
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
Hướng dẫn giải chi tiết
a) Vẽ MP song song với AC và cắt CD tại P
Ta có: \(\frac{{AM}}{{MD}} = \frac{{CP}}{{PD}} = \frac{{CN}}{{NC'}}\)
Do đó PN // DC′ // AB′
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có MP // AC và PN // AB′. Vậy mặt phẳng(MNP) song song với mặt phẳng (ACB’) và do đó MN // (ACB′)
b) Vì mặt phẳng (MNP) song song với mặt phẳng (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ NQ // CB′, QR // C′A′ (// CA), RS //AB′ (// PN) và tất nhiên SM // QN. Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: MP // RQ, PN //SR, NQ // MS.
-- Mod Toán 11 HỌC247
-


Nêu cách xác định thiết diện được tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ.
bởi Thanh Thanh
 25/02/2021
Theo dõi (0) 1 Trả lời
25/02/2021
Theo dõi (0) 1 Trả lời -


Phát biểu định lí Ta – lét trong không gian.
bởi Nguyễn Trung Thành
 26/02/2021
Theo dõi (0) 1 Trả lời
26/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2.39 trang 81 SBT Hình học 11
Bài tập 2.40 trang 81 SBT Hình học 11
Bài tập 2.42 trang 82 SBT Hình học 11
Bài tập 2.43 trang 82 SBT Hình học 11
Bài tập 2.44 trang 82 SBT Hình học 11
Bài tập 2.45 trang 83 SBT Hình học 11
Bài tập 2.46 trang 83 SBT Hình học 11
Bài tập 2.47 trang 83 SBT Hình học 11
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.50 trang 84 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC