Giải bài 2 tr 77 sách GK Toán Hình lớp 11
Cho hình chóp S.ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là tâm hình bình hành, tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).
Hướng dẫn giải chi tiết bài 2
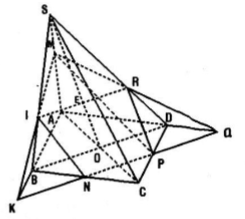
Trên mp(ABCD) gọi K là giao điểm của AB và NP. Trên mp(SAB), gọi I là giao điểm của MK và AB.
\( \Rightarrow \) M, K là 2 điểm chung của 2 mp(MNP) và (SAB)
\( \Rightarrow (MNP) \cap (SAB) = MI\)
Trên mp(ABCD) gọi Q là giao điểm của AD và NP. Trên mp (SAD) gọi R là giao điểm của MQ và SD.
\( \Rightarrow (MNP) \cap (SAD) = MR\) và \((MNP) \cap (ABCD) = NP\)
\( \Rightarrow \) Thiết diện của hình chóp khi cắt bởi mp(MNP) là ngũ giác MINPR.
Trên mp(SBD), gọi E là giao điểm của SO và IR.
Mà \({\rm{IR}} = (SBD) \cap (MNP) \Rightarrow E\) là giao điểm của SO và (MNP).
-- Mod Toán 11 HỌC247
-


Cho năm điểm \(A, B, C, D, E\) sao cho không có bốn điểm nào cùng nằm trên một mặt phẳng. Số hình tứ diện có các đỉnh lấy từ năm điểm đã cho là
bởi Thùy Nguyễn
 28/02/2021
28/02/2021
A. 5
B. 6
C. 3
D. 4
Theo dõi (0) 1 Trả lời -


A. Qua một điểm và một đường thẳng không chứa điểm đó có duy nhất một mặt phẳng.
B. Qua hai đường thẳng cắt nhau có duy nhất một mặt phẳng.
C. Qua hai đường thẳng song song có duy nhất một mặt phẳng.
D. Qua hai đường thẳng không chéo nhau có duy nhất một mặt phẳng.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 77 SGK Hình học 11
Bài tập 1 trang 77 SGK Hình học 11
Bài tập 3 trang 77 SGK Hình học 11
Bài tập 4 trang 78 SGK Hình học 11
Bài tập 1 trang 78 SGK Hình học 11
Bài tập 2 trang 78 SGK Hình học 11
Bài tập 3 trang 78 SGK Hình học 11
Bài tập 4 trang 79 SGK Hình học 11
Bài tập 5 trang 79 SGK Hình học 11
Bài tập 6 trang 79 SGK Hình học 11
Bài tập 7 trang 79 SGK Hình học 11
Bài tập 8 trang 80 SGK Hình học 11
Bài tập 9 trang 80 SGK Hình học 11
Bài tập 10 trang 80 SGK Hình học 11
Bài tập 11 trang 80 SGK Hình học 11
Bài tập 12 trang 80 SGK Hình học 11
Bài tập 2.37 trang 81 SBT Hình học 11
Bài tập 2.38 trang 81 SBT Hình học 11
Bài tập 2.39 trang 81 SBT Hình học 11
Bài tập 2.40 trang 81 SBT Hình học 11
Bài tập 2.41 trang 82 SBT Hình học 11
Bài tập 2.42 trang 82 SBT Hình học 11
Bài tập 2.43 trang 82 SBT Hình học 11
Bài tập 2.44 trang 82 SBT Hình học 11
Bài tập 2.45 trang 83 SBT Hình học 11
Bài tập 2.46 trang 83 SBT Hình học 11
Bài tập 2.47 trang 83 SBT Hình học 11
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.50 trang 84 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC






