Giải bài 2.37 tr 81 SBT Hình học 11
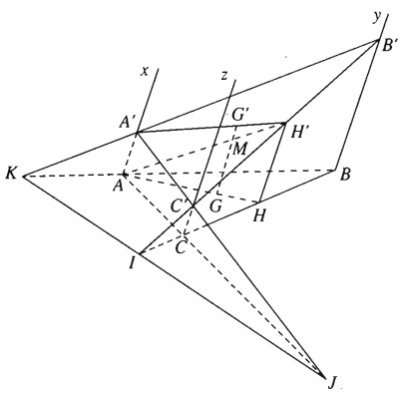
Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA' = a, trên By lấy đoạn BB' = b, trên Cz lấy đoạn CC' = c.
a) Gọi I, J và K lần lượt là các giao điểm B'C', C'A' và A'B' với (α).
Chứng minh rằng \(\frac{{IB}}{{IC}}.\frac{{JC}}{{JA}}.\frac{{KA}}{{KB}} = 1\)
b) Gọi G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C'.
Chứng minh: GG′ // AA′.
c) Tính GG' theo a, b, c
Hướng dẫn giải chi tiết
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′ \( \Rightarrow \frac{{IB}}{{IC}} = \frac{{BB'}}{{CC'}} = \frac{b}{c}\)
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′ \( \Rightarrow \frac{{JC}}{{JA}} = \frac{{CC'}}{{AA'}} = \frac{c}{a}\)
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′ \( \Rightarrow \frac{{KA}}{{KB}} = \frac{{AA'}}{{BB'}} = \frac{a}{b}\)
Do đó \(\frac{{IB}}{{IC}}.\frac{{JC}}{{JA}}.\frac{{KA}}{{KB}} = \frac{b}{c}.\frac{c}{a}.\frac{a}{b} = 1\)
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
\(\left\{ \begin{array}{l}
\frac{{AG}}{{AH}} = \frac{2}{3}\\
\frac{{A'G'}}{{A'H'}} = \frac{2}{3}
\end{array} \right. \Rightarrow AA'\parallel GG'\parallel HH'\)
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
\( \Rightarrow \frac{{G'M}}{{AA'}} = \frac{{H'G'}}{{H'A'}} = \frac{1}{3} \Rightarrow G'M = \frac{1}{3}AA' = \frac{1}{3}a\)
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
\( \Rightarrow \frac{{MG}}{{HH'}} = \frac{{AG}}{{AH}} = \frac{2}{3} \Rightarrow MG = \frac{2}{3}HH'\)
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
\(HH' = \frac{{BB' + CC'}}{2} = \frac{{b + c}}{2} \Rightarrow MG = \frac{2}{3}HH' = \frac{2}{3}.\frac{{b + c}}{2} = \frac{1}{3}\left( {b + c} \right)\)
Do đó \(GG' = G'M + MG = \frac{1}{3}a + \frac{1}{3}\left( {b + c} \right) = \frac{1}{3}\left( {a + b + c} \right)\).
-- Mod Toán 11 HỌC247
-


Trong không gian, cho ba đường thẳng phân biệt \(a,\;b,\;c\) trong đó \(a\,\parallel \,b\). Khẳng định nào sau đây sai ?
bởi Lan Ha
 25/02/2021
25/02/2021
A. Nếu \(a\,\parallel \,c\) thì \(b\,\parallel \,c\).
B. Nếu \(c\) cắt \(a\) thì \(c\) cắt \(b\).
C. Nếu \(A \in a\) và \(B \in b\) thì ba đường thẳng \(a,\;b,\;AB\) cùng ở trên một mặt phẳng.
D. Tồn tại duy nhất một mặt phẳng qua \(a\) và \(b\).
Theo dõi (0) 1 Trả lời -


Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy \(A, B\) thuộc a và \(C, D\) thuộc b. Khẳng định nào sau đây đúng khi nói về hai đường thẳng AD và BC?
bởi Nguyễn Thị Thúy
 25/02/2021
25/02/2021
A. Có thể song song hoặc cắt nhau.
B. Cắt nhau.
C. Song song với nhau.
D. Chéo nhau.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 11 trang 80 SGK Hình học 11
Bài tập 12 trang 80 SGK Hình học 11
Bài tập 2.38 trang 81 SBT Hình học 11
Bài tập 2.39 trang 81 SBT Hình học 11
Bài tập 2.40 trang 81 SBT Hình học 11
Bài tập 2.41 trang 82 SBT Hình học 11
Bài tập 2.42 trang 82 SBT Hình học 11
Bài tập 2.43 trang 82 SBT Hình học 11
Bài tập 2.44 trang 82 SBT Hình học 11
Bài tập 2.45 trang 83 SBT Hình học 11
Bài tập 2.46 trang 83 SBT Hình học 11
Bài tập 2.47 trang 83 SBT Hình học 11
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.50 trang 84 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC