Giải bài 2.38 tr 81 SBT Hình học 11
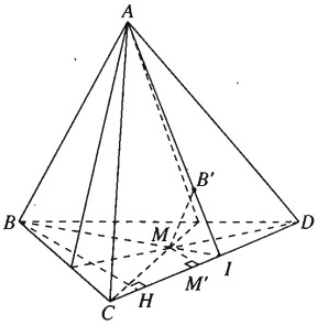
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B'.
Chứng minh rằng AB', BM và CD đồng quy tại một điểm.
b) Chứng minh \(\frac{{MB'}}{{BA}} = \frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C' và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D'. Chứng minh rằng\(\frac{{MB'}}{{BA}} + \frac{{MC'}}{{CA}} + \frac{{MD'}}{{DA}} = 1\)
Hướng dẫn giải chi tiết
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD); I ∈ AB′ ⇒ I ∈ (ACD)
Suy ra I ∈ (BCD) ∩ (ACD) = CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB ⇒ \(\frac{{MB'}}{{AB}} = \frac{{IM}}{{IB}}\)
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH \( \Rightarrow \frac{{IM}}{{IB}} = \frac{{MM'}}{{BH}}\)
Mặt khác:
\(\begin{array}{l}
\left\{ \begin{array}{l}
dt\left( {\Delta MCD} \right) = \frac{1}{2}CD.MM'\\
dt\left( {\Delta BCD} \right) = \frac{1}{2}CD.BH
\end{array} \right.\\
\frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}} = \frac{{\frac{1}{2}CD.MM'}}{{\frac{1}{2}CD.BH}} = \frac{{MM'}}{{BH}}
\end{array}\)
Do đó: \(\frac{{MB'}}{{AB}} = \frac{{IM}}{{IB}} = \frac{{MM'}}{{BH}} = \frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
Vậy \(\frac{{MB'}}{{BA}} = \frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
c) Tương tự ta có: \(\frac{{MC'}}{{CA}} = \frac{{dt\left( {\Delta MBD} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
\(\frac{{MD'}}{{DA}} = \frac{{dt\left( {\Delta MBC} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
Vậy:
\(\begin{array}{l}
\frac{{MB'}}{{BA}} + \frac{{MC'}}{{CA}} + \frac{{MD'}}{{DA}} = \frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}} + \frac{{dt\left( {\Delta MBD} \right)}}{{dt\left( {\Delta BCD} \right)}} + \frac{{dt\left( {\Delta MBC} \right)}}{{dt\left( {\Delta BCD} \right)}}\\
= \frac{{dt\left( {\Delta MCD} \right) + dt\left( {\Delta MBD} \right) + dt\left( {\Delta MBC} \right)}}{{dt\left( {\Delta BCD} \right)}} = \frac{{dt\left( {\Delta BCD} \right)}}{{dt\left( {\Delta BCD} \right)}} = 1
\end{array}\)
-- Mod Toán 11 HỌC247
-


A. Hai đường thẳng chéo nhau thì chúng có điểm chung.
B. Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
C. Hai đường thẳng song song với nhau thì có thể chéo nhau.
D. Khi hai đường thẳng ở trên hai mặt phẳng phân biệt thì hai đường thẳng đó chéo nhau.
Theo dõi (0) 1 Trả lời -


Trong các mệnh đề sau về hai đường thẳng cùng song song, mệnh đề nào đúng?
bởi Nguyễn Tiểu Ly
 26/02/2021
26/02/2021
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng nhau.
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt phẳng song song.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 12 trang 80 SGK Hình học 11
Bài tập 2.37 trang 81 SBT Hình học 11
Bài tập 2.39 trang 81 SBT Hình học 11
Bài tập 2.40 trang 81 SBT Hình học 11
Bài tập 2.41 trang 82 SBT Hình học 11
Bài tập 2.42 trang 82 SBT Hình học 11
Bài tập 2.43 trang 82 SBT Hình học 11
Bài tập 2.44 trang 82 SBT Hình học 11
Bài tập 2.45 trang 83 SBT Hình học 11
Bài tập 2.46 trang 83 SBT Hình học 11
Bài tập 2.47 trang 83 SBT Hình học 11
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.50 trang 84 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC