Giải bài 2.50 tr 84 SBT Hình học 11
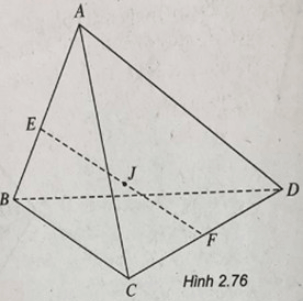
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho MA2 + MB2 + MC2 + MD2 đạt giá trị cực tiểu.
Hướng dẫn giải chi tiết
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
\(\begin{array}{l}
M{A^2} + M{B^2} = 2M{E^2} + \frac{1}{2}A{B^2}\,\,\left( 1 \right)\\
M{C^2} + M{D^2} = 2M{F^2} + \frac{1}{2}C{D^2}\,\,\left( 2 \right)
\end{array}\)
Cộng (1) và (2) ta có:
\(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2\left( {M{E^2} + M{F^2}} \right) + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)\)
Gọi J là trung điểm của EF, ta có:
\(M{E^2} + M{F^2} = 2M{J^2} + \frac{1}{2}E{F^2}\)
Khi đó:
\(\begin{array}{l}
M{A^2} + M{B^2} + M{C^2} + M{D^2}\\
= 2\left( {2M{J^2} + \frac{1}{2}E{F^2}} \right) + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)\\
\ge E{F^2} + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)
\end{array}\)
Vậy MA2 + MB2 + MC2 + MD2 đạt giá trị nhỏ nhất khi M ≡ J.
-- Mod Toán 11 HỌC247
-


Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm SA và SD. Lấy điểm K trên cạnh SB sao cho 2BK=SK. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
bởi Đoàn Diệu Linh
 27/03/2020
ai giải giúp mình 2 bài này với ạ :(
27/03/2020
ai giải giúp mình 2 bài này với ạ :( Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Chứng minh ba vecto MN, PQ, AB đồng phẳng biết trên MQ lấy điểm A sao cho MA =3AQ
bởi Nhung Nhung
 07/02/2020
cho tứ diện MNPQ, trên MQ lấy điểm A sao cho MA =3AQ, trên NP lấy điểm B sao cho BP=-1/2 BN. Chứng minh ba vecto MN, PQ, AB đồng phẳngTheo dõi (0) 0 Trả lời
07/02/2020
cho tứ diện MNPQ, trên MQ lấy điểm A sao cho MA =3AQ, trên NP lấy điểm B sao cho BP=-1/2 BN. Chứng minh ba vecto MN, PQ, AB đồng phẳngTheo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2.48 trang 83 SBT Hình học 11
Bài tập 2.49 trang 83 SBT Hình học 11
Bài tập 2.51 trang 84 SBT Hình học 11
Bài tập 2.52 trang 84 SBT Hình học 11
Bài tập 2.53 trang 84 SBT Hình học 11
Bài tập 2.54 trang 84 SBT Hình học 11
Bài tập 2.55 trang 84 SBT Hình học 11
Bài tập 2.56 trang 85 SBT Hình học 10
Bài tập 2.57 trang 85 SBT Hình học 11
Bài tập 2.58 trang 85 SBT Hình học 11
Bài tập 2.59 trang 85 SBT Hình học 11
Bài tập 2.60 trang 85 SBT Hình học 11
Bài tập 2.61 trang 85 SBT Hình học 11
Bài tập 2.62 trang 86 SBT Hình học 11
Bài tập 2.63 trang 86 SBT Hình học 11
Bài tập 2.64 trang 86 SBT Hình học 11
Bài tập 2.65 trang 86 SBT Hình học 11
Bài tập 2.66 trang 86 SBT Hình học 11
Bài tập 2.67 trang 86 SBT Hình học 11
Bài tập 2.68 trang 87 SBT Hình học 11
Bài tập 2.69 trang 87 SBT Hình học 11
Bài tập 2.70 trang 87 SBT Hình học 11
Bài tập 1 trang 77 SGK Hình học 11 NC
Bài tập 2 trang 77 SGK Hình học 11 NC
Bài tập 3 trang 77 SGK Hình học 11 NC
Bài tập 4 trang 78 SGK Hình học 11 NC
Bài tập 5 trang 78 SGK Hình học 11 NC
Bài tập 6 trang 78 SGK Hình học 11 NC
Bài tập 7 trang 78 SGK Hình học 11 NC
Bài tập 8 trang 78 SGK Hình học 11 NC
Bài tập 1 trang 78 SGK Hình học 11 NC
Bài tập 2 trang 79 SGK Hình học 11 NC
Bài tập 3 trang 79 SGK Hình học 11 NC
Bài tập 4 trang 79 SGK Hình học 11 NC
Bài tập 5 trang 79 SGK Hình học 11 NC
Bài tập 6 trang 79 SGK Hình học 11 NC
Bài tập 7 trang 79 SGK Hình học 11 NC
Bài tập 8 trang 80 SGK Hình học 11 NC
Bài tập 9 trang 80 SGK Hình học 11 NC
Bài tập 10 trang 80 SGK Hình học 11 NC