Phần hướng dẫn giải bài tập Hình học 11 Ôn tập chương II Đường thẳng và mặt phẳng trong không gian - Quan hệ song song sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 11 Cơ bản và Nâng cao.
-
Bài tập 1 trang 77 SGK Hình học 11
Hãy nêu những cách xác định mặt phẳng, kí hiệu mặt phẳng.
-
Bài tập 2 trang 77 SGK Hình học 11
Thế nào là đường thẳng song song với đường thẳng? Đường thẳng song song với mặt phẳng? Mặt phẳng song song với mặt phẳng.
-
Bài tập 3 trang 77 SGK Hình học 11
Nêu phương pháp chứng minh 3 điểm thẳng hàng?
-
Bài tập 4 trang 77 SGK Hình học 11
Nêu phương pháp chứng minh ba đường thẳng đồng quy?
-
Bài tập 5 trang 77 SGK Hình học 11
Nêu phương pháp chứng minh:
- Đường thẳng song song với đường thẳng.
- Đương thẳng song song với mặt phẳng.
- Mặt phẳng song song với mặt phẳng.
-
Bài tập 6 trang 77 SGK Hình học 11
Phát biểu định lí Ta-let trong không gian.
-
Bài tập 7 trang 77 SGK Hình học 11
Nêu cách xác định thiết diện tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ.
-
Bài tập 1 trang 77 SGK Hình học 11
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.
a) Tìm giao tuyến của các mặt phẳng: (AEC) và (BFD); (BCE) và (ADF)
b) Lấy M là điểm thuộc đoạn DF. Tìm giao điểm của đường tẳng AM với mặt phẳng (BCE)
c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
-
Bài tập 2 trang 77 SGK Hình học 11
Cho hình chóp S.ABCD là hình bình hành. Gọi M, N, P theo thứ tự là trung điểm của SA, BC, CD. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). Gọi O là tâm hình bình hành, tìm giao điểm của đường thẳng SO với mặt phẳng (MNP).
-
Bài tập 3 trang 77 SGK Hình học 11
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M. N theo thứ tự là trung điểm của các cạnh SB và SC
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
-
Bài tập 4 trang 78 SGK Hình học 11
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn nửa đường thẳng Ax,By, Cz, Dt ở cùng phía đối với mặt phẳng (ABCD), song song với nhau và không nằm trong mặt phẳng (ABCD). Một mặt phẳng \((\beta )\) lần lượt cắt Ax, By, Cz và Dt tại A’, B’, C’ và D’.
a) Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt)
b) Gọi \(I = AC \cap BD,J = A'C'\, \cap \,B'D'.\) Chứng minh IJ song song với AA’.
c) Cho \({\rm{AA}}' = a,BB' = b,CC' = c.\) Hãy tính DD’.
-
Bài tập 1 trang 78 SGK Hình học 11
Tìm mệnh đề sai trong các mệnh đề sau đây:
(A) Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa;
(B) Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau;
(C) Nếu hai đường thẳng song song với một mặt phẳng thì song song với nhau
(D) Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại.
-
Bài tập 2 trang 78 SGK Hình học 11
Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó.
(A) Đồng quy
(B) Tạo thành tam giác;
(C) Trùng nhau
(D) Cùng song song với một mặt phẳng
Tìm mệnh đề đúng trong các mệnh đề trên.
-
Bài tập 3 trang 78 SGK Hình học 11
Cho tứ diện ABCD. Gọi I, J và K lần lượt là trung điểm của AC, BC và BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
.jpg)
(A) KD
(B) KI
(C) Đường thẳng qua K và song song với AB
(D) Không có
-
Bài tập 4 trang 79 SGK Hình học 11
Tìm mệnh đề đúng trong các mệnh đề sau:
(A) Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong \((\alpha )\) đều song song với \((\beta )\) ;
(B) Nếu hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau thì mọi đường thẳng nằm trong \((\alpha )\) đều song song với mọi đường thẳng nằm trong \((\beta )\) ;
(C) Nếu hai đường thẳng song song với nhau lần lượt nằm trong hai mặt phẳng phân biệt \((\alpha )\) và \((\beta )\) thì \((\alpha )\) và \((\beta )\) song song với nhau;
(D) Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
-
Bài tập 5 trang 79 SGK Hình học 11
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC. E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
(A) Tam giác MNE;
(B) Tứ giác MNEF với F là điểm bất kì trên cạnh BD;
(C) Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC
(D) Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC.
-
Bài tập 6 trang 79 SGK Hình học 11
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi I, J lần lượt là trọng tâm của tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là:
(A) Tam giác cân
(B) Tam giác vuông
(C) Hình thang
(D) Hình bình hành
-
Bài tập 7 trang 79 SGK Hình học 11
Cho tứ diện đều SABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng \((\alpha )\) song song với (SIC). Thiết diện tạo bởi \((\alpha )\) và tứ diện SABC là:
(A) Tam giác cân tại M
(B) Tam giác đều
(C) Hình bình hành
(D) Hình thoi
-
Bài tập 8 trang 80 SGK Hình học 11
Với giả thiết của bài tập 7, chu vi của thiết diện tính theo AM = x là:
(A) \(x(1 + \sqrt {3)} \) (B) \(2x(1 + \sqrt 3 )\)
(C) \(3x(1 + \sqrt 3 )\) (D) Không tính được
-
Bài tập 9 trang 80 SGK Hình học 11
Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng song song với nhau lần lượt đi qua B, C, D và nằm về một phía của mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt Bx, Cy, Dz lần lượt tại B', C' D' với BB' = 2, DD' = 4. Khi đó CC' bằng
(A) 3
(B) 4
(C) 5
(D) 6.
-
Bài tập 10 trang 80 SGK Hình học 11
Tìm mệnh đề đúng trong các mệnh đề sau:
(A) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau;
(B) Hai đường thẳng phân biệt không cắt nhau thì chéo nhau;
(C) Hai đường thẳng phân biệt không song song thì chéo nhau;
(D) Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau.
-
Bài tập 11 trang 80 SGK Hình học 11
Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng \(\left( \alpha \right)\) song song với (SBC). Thiết diện tạo bởi \(\left( \alpha \right)\) và hình chóp S.ABCD là hình gì?
(A) Tam giác;
(B) Hình bình hành
(C) Hình thang
(D) Hình vuông
-
Bài tập 12 trang 80 SGK Hình học 11
Với giả thiết của bài tập 11, gọi N, P, Q lần lượt là giao của mặt phẳng \(\left( \alpha \right)\) với các đường thẳng CD, DS, SA. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
(A) Đường thẳng
(B) Nửa đường thẳng
(C) Đoạn thẳng song song với AB
(D) Tập hợp rỗng
-
Bài tập 2.37 trang 81 SBT Hình học 11
Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA' = a, trên By lấy đoạn BB' = b, trên Cz lấy đoạn CC' = c.
a) Gọi I, J và K lần lượt là các giao điểm B'C', C'A' và A'B' với (α).
Chứng minh rằng \(\frac{{IB}}{{IC}}.\frac{{JC}}{{JA}}.\frac{{KA}}{{KB}} = 1\)
b) Gọi G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C'.
Chứng minh: GG′ // AA′.
c) Tính GG' theo a, b, c
-
Bài tập 2.38 trang 81 SBT Hình học 11
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B'.
Chứng minh rằng AB', BM và CD đồng quy tại một điểm.
b) Chứng minh \(\frac{{MB'}}{{BA}} = \frac{{dt\left( {\Delta MCD} \right)}}{{dt\left( {\Delta BCD} \right)}}\)
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C' và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D'. Chứng minh rằng\(\frac{{MB'}}{{BA}} + \frac{{MC'}}{{CA}} + \frac{{MD'}}{{DA}} = 1\)
-
Bài tập 2.39 trang 81 SBT Hình học 11
Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA', BB', CC' song song cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC', A'B'C'.
a) Chứng minh (IGK) // (BB′CC′).
b) Chứng minh rằng (A′GK) // (AIB′).
-
Bài tập 2.40 trang 81 SBT Hình học 11
Cho hình hộp ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
-
Bài tập 2.41 trang 82 SBT Hình học 11
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnhAD và CC’ sao cho \(\frac{{AM}}{{MD}} = \frac{{CN}}{{NC'}}\)
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
-
Bài tập 2.42 trang 82 SBT Hình học 11
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'.
a) Chứng minh rằng hai đường chéo AC' và A'C cắt nhau và hai đường chéo BD' và B'D cắt nhau.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.
-
Bài tập 2.43 trang 82 SBT Hình học 11
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S1, S2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng MS1, MS2 cắt (α) lần lượt tại M1 và M2.
a) Chứng minh rằng M1M2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M1 và M2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
-
Bài tập 2.44 trang 82 SBT Hình học 11
Cho hình lập phương ABCD.A'B'C'D' các trung điểm E, F của các cạnh AB, DD'. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC') và (EFK) với K là trung điểm của cạnh B'C'.
-
Bài tập 2.45 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD có đáy là hình thang (đáy lớn AD). Gọi O la giao điểm của AC và BD, I và J lần lượt là trung điểm của SB và SC.
a) Xác định giao điểm M của AI và (SCD).
b) Chứng minh IJ // (SAD).
c) Xác định thiết diện của hình chóp cắt bởi mp (P) qua I, song song với SD và AC.
-
Bài tập 2.46 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C' là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C'M và song song với BC.
a) Xác định thiết diện (P) cắt hình chóp S.ABCD. Xác định vị trí điểm M để thiết diện là hình bình hành.
b) Khi M di động trên cạnh SA, thì giao điểm của hai cạnh đối của thiết diện chạy trên đường nào?
-
Bài tập 2.47 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.
a) Tìm giao điểm của MN và mặt phẳng (SAC).
b) Tìm thiết diện của hình chóp với mặt phẳng (NBC). Thiết diện đó là hình gì?
-
Bài tập 2.48 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G1 và G2 lần lượt là trọng tâm của các tam giác SBC và SCD.
a) Tìm giao tuyến của mặt phẳng (AG1G2) với các mặt phẳng (ABCD) và (SCD).
b) Xác định thiết diện của hình chóp với mặt phẳng (AG1G2).
-
Bài tập 2.49 trang 83 SBT Hình học 11
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' sao cho đường thẳng B'C' cắt đường thẳng BC tại K, đường thẳng C'D' cắt đường thẳng CD tại J, đường thẳng D'B' cắt đường thẳng DB tại I.
a) Chứng minh ba điểm I, J, K thẳng hàng.
b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
-
Bài tập 2.50 trang 84 SBT Hình học 11
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho MA2 + MB2 + MC2 + MD2 đạt giá trị cực tiểu.
-
Bài tập 2.51 trang 84 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu một mặt phẳng cắt một trong hai đường thẳng song song thì mặt phẳng đó sẽ cắt đường thẳng còn lại.
B. Hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì cắt nhau theo một giao tuyến song song với một trong hai đường thẳng đó.
C. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó sẽ cắt đường thẳng còn lại.
D. Hai mặt phẳng có một điểm chung thì cắt nhau theo một giao tuyến đi qua điểm chung nào đó.
-
Bài tập 2.52 trang 84 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
B. Hai mặt phẳng có một điểm chung thì chúng còn vô số điểm chung khác nữa.
C. Tồn tại duy nhất một mặt phẳng đi qua 3 điểm phân biệt.
D. Tồn tại duy nhất một mặt phẳng đi qua 1 điểm và một đường thẳng cho trước.
-
Bài tập 2.53 trang 84 SBT Hình học 11
Cho a ⊂ (P); b ⊂ (Q). Khẳng định nào sau đây đúng?
A. (P) // (Q) ⇒ a // b B. a // b ⇒ (P) // (Q)
C. (P) // (Q) ⇒ a // (Q), b // (P) D. a và b chéo nhau
-
Bài tập 2.54 trang 84 SBT Hình học 11
Cho đường thẳng a và mặt phẳng (P) song song với nhau. Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a là
A. 0 B. 2 C. Vô số D. 3
-
Bài tập 2.55 trang 84 SBT Hình học 11
Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó, ta có
A. a và b song song hoặc trùng nhau
B. a và b cắt nhau
C. a và b trùng nhau
D. a và b song song
-
Bài tập 2.56 trang 85 SBT Hình học 10
Khẳng định nào sau đây đúng?
A. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
B. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
C. Hai đường thẳng không có điểm chung thì song song với nhau.
D. Hai đường thẳng phân biệt lần lượt nằm trong hai mặt phẳng khác nhau thì chéo nhau.
-
Bài tập 2.57 trang 85 SBT Hình học 11
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi ấy giao tuyến của MG và mặt phẳng (ABC) là
A. Điểm N.
B. Điểm C.
C. Giao điểm của đường thẳng MG và đường thẳng BC.
D. Giao điểm của đường thẳng MG và đường thẳng AN.
-
Bài tập 2.58 trang 85 SBT Hình học 11
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAD. Mặt phẳng (GBC) cắt SD tạo E. Tỉ số SE / SD là
A. 1 B. \(\frac{1}{2}\)
C. \(\frac{2}{3}\) D. \(\frac{3}{2}\)
-
Bài tập 2.59 trang 85 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB, SAD. Lấy M là trung điểm CD. Khẳng định nào sau đây đúng?
A. IJ // (SBM) B. IJ // (SBD)
C. IJ // (SBC) D. IJ // (SCD)
-
Bài tập 2.60 trang 85 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với (β)
B. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với mọi đường thẳng trong (β)
C. Trong (α) có chứa hai đường thẳng phân biệt và hai đường thẳng này cùng song song với (β) thì (α) và (β) song song với nhau.
D. Qua một điểm nằm ngoài mặt phẳng (α) cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
-
Bài tập 2.61 trang 85 SBT Hình học 11
Cho lăng trụ ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm của tam giác ABC, A'B'C'. M là điểm trên cạnh AC sao cho AM = 2MC. Khẳng định nào sau đây sai?
A. GG' // (ACC'A') B. GG' // (ABB'A')
C. MG' // (BCC'B') ≠ ∅ D. (MGG') // (BCC'B')
-
Bài tập 2.62 trang 86 SBT Hình học 11
Cho mặt phẳng (P) và đường thẳng d ⊂ (P). Khẳng định nào sau đây đúng?
A. Nếu 3 điểm A, B, C cùng thuộc (P) và A, B, C thẳng hàng thì A, B, C ∈ d.
B. Nếu A ∉ d thì A ∉ (P).
C. Nếu A ∈ (P) thì A ∉ d.
D. ∀A, A ∈ d ⇒ A ∈ (P)
-
Bài tập 2.63 trang 86 SBT Hình học 11
Khẳng định nào sau đây sai?
A. Qua một điểm và một đường thẳng không chứa điểm đó có duy nhất một mặt phẳng.
B. Qua hai đường thẳng cắt nhau có duy nhất một mặt phẳng.
C. Qua hai đường thẳng song song có duy nhất một mặt phẳng.
D. Qua hai đường thẳng không chéo nhau có duy nhất một mặt phẳng.
-
Bài tập 2.64 trang 86 SBT Hình học 11
Cho năm điểm A, B, C, D, E sao cho không có bốn điểm nào cùng nằm trên một mặt phẳng. Số hình tứ diện có các đỉnh lấy từ năm điểm đã cho là
A. 5 B. 6 C. 3 D. 4
-
Bài tập 2.65 trang 86 SBT Hình học 11
Cho tứ diện ABCD. Trên các cạnh AB, AD lần lượt lấy các điểm M, N sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\). Gọi P, Q lần lượt là trung điểm các cạnh CD, CB.
Khẳng định nào sau đây đúng?
A. Bốn điểm M, N, P, Q không đồng phẳng.
B. Tứ giác MNPQ là hình bình hành.
C. Tứ giác MNPQ là hình thang.
D. Tứ giác MNPQ không có các cặp cạnh đối nào song song.
-
Bài tập 2.66 trang 86 SBT Hình học 11
Cho tứ giác đều ABCD. Một mặt phẳng (α) qua trung điểm của cạnh AB và lần lượt song song với AC và BD cắt tứ diện trên theo thiết diện là
A. hình chữ nhật. B. hình vuông.
C. hình thoi. D. hình thang cân.
-
Bài tập 2.67 trang 86 SBT Hình học 11
Cho hai hình bình hành ABCD và ABEF lần lượt có tâm O1, O2 và không cùng nằm trong một mặt phẳng. Khẳng định nào sau đây sai?
A. O1O2 song song với mặt phẳng (BCE).
B. O1O2 song song với mặt phẳng (BDE).
C. O1O2 song song với mặt phẳng (ADF).
D. O1O2 song song với mặt phẳng (CDE).
-
Bài tập 2.68 trang 87 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, I lần lượt là trung điểm của các cạnh AB, SC. Mặt phẳng (α) qua M song song với mặt phẳng (BID) sẽ cắt hình chóp theo thiết diện là
A. hình tam giác B. hình lục giác
C. hình tứ giác D. hình ngũ giác
-
Bài tập 2.69 trang 87 SBT Hình học 11
Trong mặt phẳng (α), cho tứ giác ABCD có O là giao điểm của AC và BD. S nằm ngoài (ABCD). Giao tuyến của (SAC) và (SBD) là
A. BD B. AC C. SO D. SC
-
Bài tập 2.70 trang 87 SBT Hình học 11
Cho hình chóp S.ABCD với I = AB ∩ CD. Giao tuyến của (SAB) và (SCD) là
A. SB B. SI C. SC D. BC
-
Bài tập 1 trang 77 SGK Hình học 11 NC
Trong các mệnh đề sau, mệnh đề nào đúng?
a. Hai đường thẳng chéo nhau thì không có điểm chung
b. Hai đường thẳng không có điểm chung thì chéo nhau
c. Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng
d. Hai đường thẳng không song song thì chéo nhau
-
Bài tập 2 trang 77 SGK Hình học 11 NC
Trong các mệnh đề sau, mệnh đề nào đúng ?
a. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
b. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau
c. Hai mặt phẳng phân biệt không song song thì cắt nhau
d.Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau
e. Một đường thẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại
f. Một mặt phẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại
g. Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại
-
Bài tập 3 trang 77 SGK Hình học 11 NC
Trong các hình sau, hình nào là hình biểu diễn của một tứ diện?
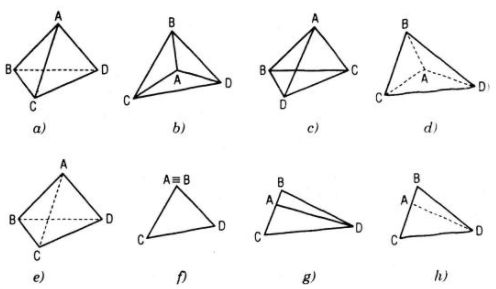
-
Bài tập 4 trang 78 SGK Hình học 11 NC
Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
a. MN // DE
b. M1N1 // mp(DEF)
c. mp(MNN1M1) // mp(DEF)
-
Bài tập 5 trang 78 SGK Hình học 11 NC
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’. Một mặt phẳng (α) cắt các cạnh AA’, BB’, CC, GG’ lần lượt tại A1, B1, C1 và G1. Chứng minh rằng:
a. GG’ song song và bằng cạnh bên của hình lăng trụ
b. G1 là trọng tâm của tam giác A1B1C1
c. \({G_1}G' = \frac{1}{3}\left( {{A_1}A' + {B_1}B' + {C_1}C'} \right);\)
\({G_1}G = \frac{1}{3}({A_1}A + {B_1}B + {C_1}C)\)
-
Bài tập 6 trang 78 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’. Vẽ thiết diện của hình hộp tạo bởi mặt phẳng đi qua hai trung điểm M, N của các cạnh AB, AD và tâm O của mặt CDD’C’
-
Bài tập 7 trang 78 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \(\frac{{AM}}{{AB}} = \frac{{D\prime N}}{{D\prime D}} = \frac{{B\prime P}}{{B\prime C\prime }}\)
a. Chứng minh rằng mp(MNP) và mp(AB'D’) song song với nhau
b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)
-
Bài tập 8 trang 78 SGK Hình học 11 NC
Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = kBN (k > 0 cho trước)
a. Chứng minh rằng MN song song với một mặt phẳng cố định
b. Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = kIN
-
Bài tập 1 trang 78 SGK Hình học 11 NC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm tam giác BCD. Khi ấy, giao điểm của đường thẳng MG và mp(ABC) là :
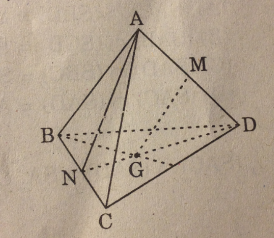
A. Điểm C
B. Giao điểm của đường thẳng MG và đường thẳng AN
C. Điểm N
D. Giao điểm của đường thẳng MG và đường thẳng BC
-
Bài tập 2 trang 79 SGK Hình học 11 NC
Cho tứ diện ABCD và ba điểm E, F, G lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là :
A. Một đoạn thẳng’
B. Một tam giác
C. Một tứ giác
D. Một ngũ giác
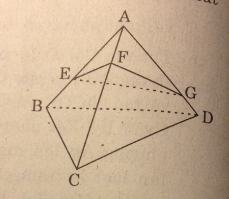
-
Bài tập 3 trang 79 SGK Hình học 11 NC
Cho tứ diện ABCD và ba điểm I, J, K lần lượt nằm trên ba cạnh AB, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(IJK) là :
A. Một tam giác
B. Một tứ giác
C. Một hình thang
D. Một ngũ giác
-
Bài tập 4 trang 79 SGK Hình học 11 NC
Cho hình chóp S.ABCD. Gọi AC ∩ BD = I, AB ∩ CD = J, AD ∩ BC = K. Đẳng thức nào sai trong các đẳng thức sau đây ?
A. (SAD) ∩ (SBD) = SI
B. (SAD) ∩ (SCD) = SJ
C. (SAD) ∩ (SBC) = SK
D. (SAC) ∩ (SAD) = AB
-
Bài tập 5 trang 79 SGK Hình học 11 NC
Cho hình chóp S.ABCD. Một mặt phẳng không đi qua đỉnh nào của hình chóp cắt các cạnh SA, SB, SC, SD lần lượt tại A’, B’, C’, D’. Gọi O là giao điểm AC và BD. Tìm mệnh đề đúng trong các mệnh đề sau đây
A. Các đường thẳng A’C’, B’D’, SO đôi một chéo nhau
B. Các đường thẳng A’C, B’D’, SO đồng phẳng
C. Các đường thẳng A’C’, B’D’, SO đồng quy
D. Hai đường thẳng A’C’ và B’D’ cắt nhau còn hai đường thẳng A’C’ và SO chéo nhau
-
Bài tập 6 trang 79 SGK Hình học 11 NC
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng ?
A. Đường thẳng GE song song với đường thẳng CD
B. Đường thẳng GE cắt đường thẳng CD
C. Hai đường thẳng GE và CD chéo nhau
D. Đường thẳng GE cắt đường thẳng AD
-
Bài tập 7 trang 79 SGK Hình học 11 NC
Cho tứ diện ABCD. Gọi M, K lần lượt là trung điểm của BC và AC, N là điểm trên cạnh BD sao cho BN = 2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau đây, mệnh đề nào đúng ?
A. AF = FD
B. AF = 2FD
C. AF = 3FD
D. FD = 2AF
-
Bài tập 8 trang 80 SGK Hình học 11 NC
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :
A. \(\frac{{{a^2}\sqrt 3 }}{2}\)
B. \(\frac{{{a^2}\sqrt 2 }}{4}\)
C. \(\frac{{{a^2}\sqrt 2 }}{6}\)
D. \(\frac{{{a^2}\sqrt 3 }}{4}\)
-
Bài tập 9 trang 80 SGK Hình học 11 NC
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của AB và CB. Khi ấy, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với :
A. Đường thẳng AD
B. Đường thẳng BJ
C. Đường thẳng BI
D. Đường thẳng IJ
-
Bài tập 10 trang 80 SGK Hình học 11 NC
Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Tìm mệnh đề đúng trong các mệnh đề sau đây :
A. A’B’ // mp(SAD)
B. A’C’ // mp(SBD)
C. mp(A’C’D’) // mp(ABC)
D. A’C’ // BD
-
Bài tập 11 trang 80 SGK Hình học 11 NC
Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là:
A. \(\frac{{{m^2}\sqrt 3 }}{4}\)
B. \(\frac{{{{\left( {a - m} \right)}^2}\sqrt 2 }}{2}\)
C. \(\frac{{{{\left( {a + m} \right)}^2}}}{4}\)
D. \(\frac{{{{\left( {a - m} \right)}^2}\sqrt 3 }}{4}\)
-
Bài tập 12 trang 80 SGK Hình học 11 NC
Cho hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) song song với AC và SB lần lượt cắt các cạnh SA, AB, BC, SC, SD, BD tại M, N, E, F, I, J. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
A. Bốn đường thẳng MN, EF, IJ, SB đôi một song song
B. Bốn đường thẳng MN, EF, IJ, SB đồng quy
C. Bốn đường thẳng MN, EF, IJ, SB đồng phẳng
D. Cả ba mệnh đề trên đều sai.

.JPG)






