Giải bài 4 tr 122 sách GK Toán ĐS & GT lớp 11
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh dấu 1, 2, 3, ..., n trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó.
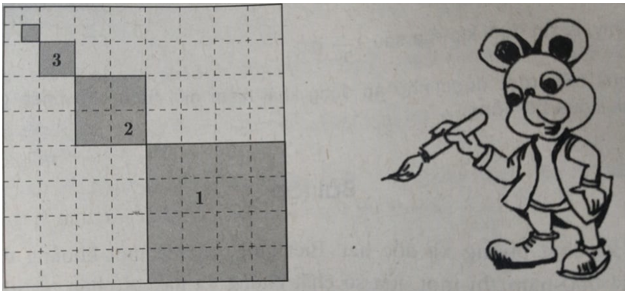
Giả sử quy trình tô màu của Mickey có thể tiến ra vô hạn.
a) Gọi un là diện tích của hình vuông màu xám thứ n. Tính \(u_1 , u_2 , u_3\) và \(u_n\).
b) Tính lim\(S_n\) với \(S_n = u_1 + u_2 + u_3 + ... + u_n\) .
Hướng dẫn giải chi tiết bài 4
Câu a:
Do miếng bìa hình vuông đã cho có cạnh bằng 1 nên hình vuông màu xám thứ 1 có cạnh bằng \(\frac{1}{2}\) do đó diện tích hình vuông thứ nhất: \(u_1=\left ( \frac{1}{2} \right )^2\)
Tương tự như trên ta có \(u_2=\left ( \frac{1}{4} \right )^2=\left ( \frac{1}{2} \right )^4, u_3=\left ( \frac{1}{8} \right )^2=\left ( \frac{1}{2} \right )^6, u_n=\left (\frac{1}{2} \right )^{2n}\)
Câu b:
Ta có \({S_n} = {u_1} + {u_2} + ... + {u_n} = {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^4} + ... + {\left( {\frac{1}{2}} \right)^2}^n = \frac{1}{4} + {\left( {\frac{1}{4}} \right)^2} + ...{\left( {\frac{1}{4}} \right)^n}\)
Dễ thấy đây là Cấp số nhân lùi vô hạn có \({u_1} = \frac{1}{4}\) và công bội \(q = \frac{1}{4}\)
Vậy: \({S_n} = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{1}{4}}}{{1 - \frac{1}{4}}} = \frac{1}{3}.\)
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 4 SGK
-


Thực hiện tính giới hạn của dãy số có số hạng tổng quát sau đây, khi \(\displaystyle n \to + \infty \): \(\displaystyle {u_n} = {2^n} + {1 \over n}\)
bởi Nguyen Phuc
 26/04/2022
Theo dõi (0) 1 Trả lời
26/04/2022
Theo dõi (0) 1 Trả lời -


Thực hiện tính giới hạn của dãy số có số hạng tổng quát sau đây, khi \(\displaystyle n \to + \infty \): \(\displaystyle {c_n} = {{2n\sqrt n } \over {{n^2} + 2n - 1}}\)
bởi Nguyễn Vân
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Thực hiện tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi \(\displaystyle n \to + \infty \): \(\displaystyle {b_n} = {{3{n^3} - 5n + 1} \over {{n^2} + 4}}\)
bởi Lê Viết Khánh
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Thực hiện tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi \(\displaystyle n \to + \infty \): \(\displaystyle {a_n} = {{2n - 3{n^3} + 1} \over {{n^3} + {n^2}}}\)
bởi hi hi
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Cho biết rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn hữu hạn, còn dãy số \(\left( {{v_n}} \right)\) không có giới hạn hữu hạn. Cho biết dãy số \(\left( {{u_n} + {v_n}} \right)\) có thể có giới hạn hữu hạn không ?
bởi Bánh Mì
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 121 SGK Đại số & Giải tích 11
Bài tập 3 trang 121 SGK Đại số & Giải tích 11
Bài tập 5 trang 122 SGK Đại số & Giải tích 11
Bài tập 6 trang 122 SGK Đại số & Giải tích 11
Bài tập 7 trang 122 SGK Đại số & Giải tích 11
Bài tập 8 trang 122 SGK Đại số & Giải tích 11
Bài tập 4.1 trang 156 SBT Toán 11
Bài tập 4.2 trang 156 SBT Toán 11
Bài tập 4.3 trang 156 SBT Toán 11
Bài tập 4.4 trang 156 SBT Toán 11
Bài tập 4.5 trang 156 SBT Toán 11
Bài tập 4.6 trang 157 SBT Toán 11
Bài tập 4.7 trang 157 SBT Toán 11
Bài tập 4.8 trang 157 SBT Toán 11
Bài tập 4.9 trang 157 SBT Toán 11
Bài tập 4.10 trang 157 SBT Toán 11
Bài tập 4.11 trang 157 SBT Toán 11
Bài tập 4.12 trang 157 SBT Toán 11
Bài tập 4.13 trang 157 SBT Toán 11
Bài tập 4.14 trang 157 SBT Toán 11
Bài tập 4.15 trang 157 SBT Toán 11
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





