Bài tập 14 trang 142 SGK Toán 11 NC
Chứng minh rằng nếu q > 1 thì \(\lim {q^n} = + \infty \).
Hướng dẫn giải chi tiết
Ta có:
\(\lim {\left( {\frac{1}{q}} \right)^n} = 0\) (do q > 1) mà q > 0 nên \(\lim {q^n} = + \infty \).
-- Mod Toán 11 HỌC247
Nếu bạn thấy
hướng dẫn giải
Bài tập 14 trang 142 SGK Toán 11 NC HAY thì click chia sẻ
YOMEDIA
-
Tính lim (2n.căn n+1)/(n^2+n+3)
bởi Thủy Em
09/01/2020
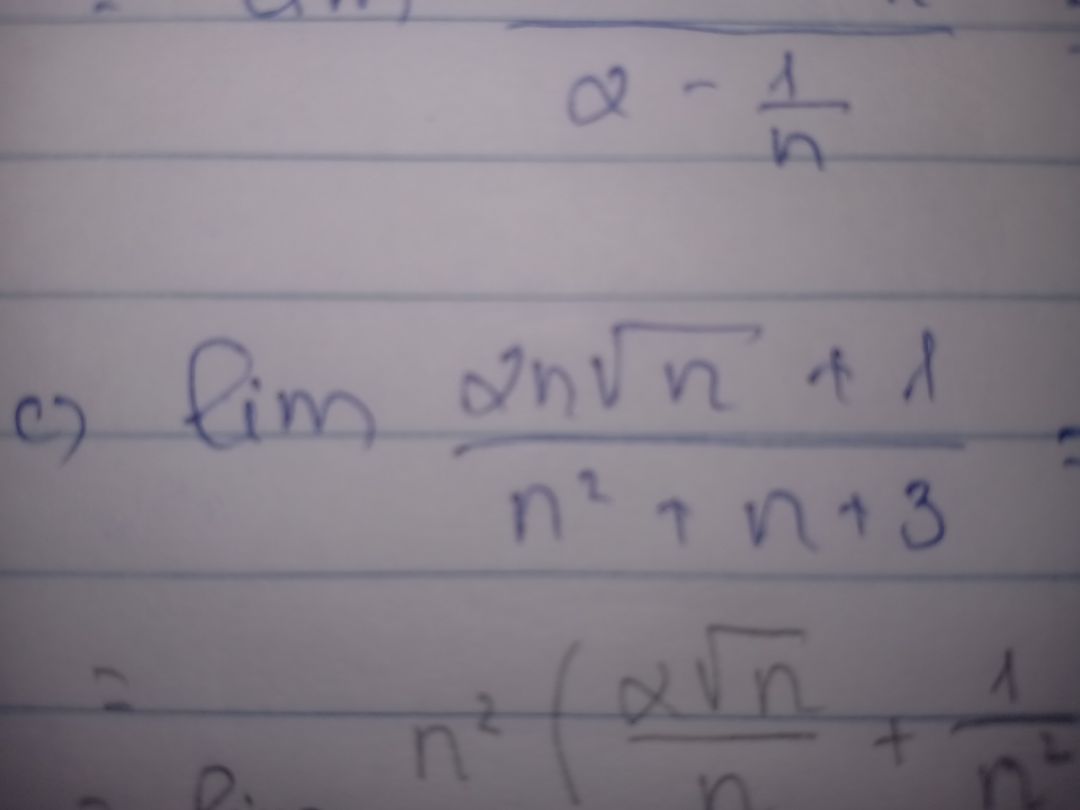Theo dõi (0) 2 Trả lời -
Tính lim n(căn(n^2+2)-căn(n^2-4))
bởi Vy Linh
08/01/2020
Theo dõi (1) 1 Trả lời -
Tìm lim sin n/căn n
bởi Như Trúc
08/01/2020
Lim sinn/√nTheo dõi (0) 1 Trả lời -
Tính lim (1+2+...+n)/n^2
bởi Tâm Thanh
07/01/2020
Giải giúp mình ạ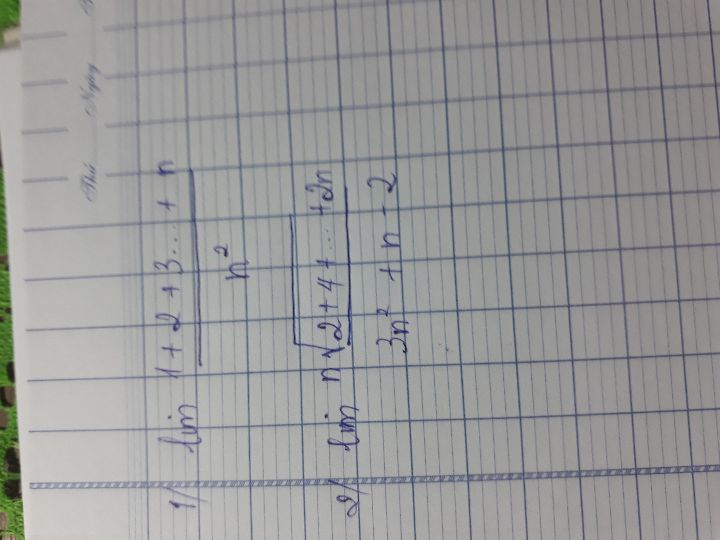
Theo dõi (0) 0 Trả lời -
Tính lim (3^n-4^n+1)/(2.4^n+2^n)
bởi Nguyễn Ngọc Khánh Vy
07/01/2020
Tính các giới hạn:
Theo dõi (0) 0 Trả lời
