Bài tập 4 trang 130 SGK Toán 11 NC
Cho dãy số (un) với \({u_n} = \frac{n}{{{3^n}}}\)
a. Chứng minh rằng \(\frac{{{u_{n + 1}}}}{{{u_n}}} \le \frac{2}{3}\) với mọi n.
b. Bằng phương pháp qui nạp, chứng minh rằng \(0 < {u_n} \le {\left( {\frac{2}{3}} \right)^n}\) với mọi n.
c. Chứng minh rằng dãy số (un) có giới hạn 0.
Hướng dẫn giải chi tiết
a) Ta có
\(\begin{array}{l}
\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{n + 1}}{{{3^{n + 1}}}}:\frac{n}{{{3^n}}}\\
= \frac{1}{3}.\frac{{n + 1}}{n} = \frac{1}{3}.\left( {1 + \frac{1}{n}} \right) \le \frac{2}{3},\forall n \ge 1
\end{array}\)
b) Rõ ràng \({u_n} > 0,\forall n \ge 1\).
Ta chứng minh \({u_n} \le {\left( {\frac{2}{3}} \right)^n}\,\,\,\,\left( 1 \right)\)
- Với n = 1 ta có \({u_1} = \frac{1}{3} \le \frac{2}{3}\)
Vậy (1) đúng với n = 1
- Giả sử (1) đúng với n = k, tức là ta có \({u_k} \le {\left( {\frac{2}{3}} \right)^k}\)
Khi đó \({u_{k + 1}} \le \frac{2}{3}{u_k}\) (theo câu a)
\( \Rightarrow {u_{k + 1}} \le \frac{2}{3}.{\left( {\frac{2}{3}} \right)^k} = {\left( {\frac{2}{3}} \right)^{k + 1}}\)
Vậy (1) đúng với n = k+1 nên (1) đúng với mọi n.
c) Ta có \(0 < {u_n} \le {\left( {\frac{2}{3}} \right)^n} \Rightarrow \left| {{u_n}} \right| \le {\left( {\frac{2}{3}} \right)^n}\)
Mà \(\lim {\left( {\frac{2}{3}} \right)^n} = 0 \Rightarrow \lim \left| {{u_n}} \right| = 0 \Rightarrow \lim {u_n} = 0\)
-- Mod Toán 11 HỌC247
-


Tìm giới hạn lim n^4/(n + 1)(2 + n)(n^2 +1)
bởi Nhi Nguyễn
 20/02/2020
20/02/2020
Tìm các giới hạn sau:
1. lim (n4) / ( (n + 1)(2 + n)(n2 + 1) )
2. lim (-n2 + n - 1) / (2n2 - 1)
3. lim (√(4n - 1)) / (√(n) + 1)
4. lim (2n - 3) / (3√(n3 - 2n) + 1)
5. lim (2n4 + n2 - 3) / (3n3 - 2n2 + 1)
6. lim (3n3 + 2n2 + n) / (4 - n2)
Theo dõi (0) 2 Trả lời -


Tính lim (-1)^n/n+3
bởi Phuong Ly
 19/02/2020
lim (-1)^n/n 3Theo dõi (0) 0 Trả lời
19/02/2020
lim (-1)^n/n 3Theo dõi (0) 0 Trả lời -


Tính giá trị lim (1/2 +1+ 2/3 +...+ n/2)/(n^2 +1)
bởi Hách
 18/02/2020
18/02/2020
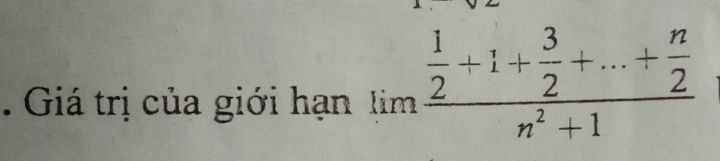 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính lim (sin(2n))/(n+1)
bởi Phan Thị Thùy Nhung
 18/02/2020
18/02/2020
Lim (sin(2n))/(n+1)
Theo dõi (0) 0 Trả lời -


Kết quả của giới hạn lim 10/căn(n^4+n^2+1) là?
bởi Nguyen Ngoc Thao
 18/02/2020
Mọi người giải giúp mình câu 49 với ạ!
18/02/2020
Mọi người giải giúp mình câu 49 với ạ! Theo dõi (2) 1 Trả lời
Theo dõi (2) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





