Giải bài 4.6 tr 157 SBT Toán 11
Cho hai dãy số () và (). Chứng minh rằng nếu \(\lim {v_n} = 0\) và \(|{u_n}| \le {v_n}\) với mọi thì \(\lim {u_n} = 0\)
Hướng dẫn giải chi tiết
Chứng minh bằng định nghĩa
Vì \(\lim {v_n} = 0\) nên \(\left| {{v_n}} \right|\) có thể nhỏ hơn một số dương tùy ý từ số hạng nào đó trở đi.
Mà \(|{u_n}| \le {v_n} \le |{v_n}|\) nên \(|{u_n}| \le |{v_n}|\) với mọi n
Do đó, \(\left| {{u_n}} \right|\) cũng có thể nhỏ hơn một số dương bé tùy ý từ số hạng nào đó trở đi. Nghĩa là \(\lim {u_n} = 0\)
-- Mod Toán 11 HỌC247
-


Biết dãy số \((u_n)\) thỏa mãn \(|u_n-1| < \dfrac{1}{n^{3}}\) với mọi \(n\). Chứng minh rằng \(\lim u_n=1\).
bởi Phạm Khánh Linh
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Có \(1 kg\) chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian \(T = 24 000\) năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (\(T\) được gọi là chu kì bán rã). Gọi \((u_n)\) là khối lượng chất phóng xạ còn sót lại sau chu kì thứ \(n\). Tìm số hạng tổng quát \(u_n\) của dãy số \((u_n)\).
bởi Hoang Vu
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Giới hạn dãy số
bởi Lê Thị Hương Giang
 18/02/2021
18/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn: Iim 6n 2026/28n-27
bởi Đàm Thị Hồng Tươi
 07/02/2021
07/02/2021
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giới hạn của các dãy số
bởi Ngọc Hiền
 02/02/2021
02/02/2021
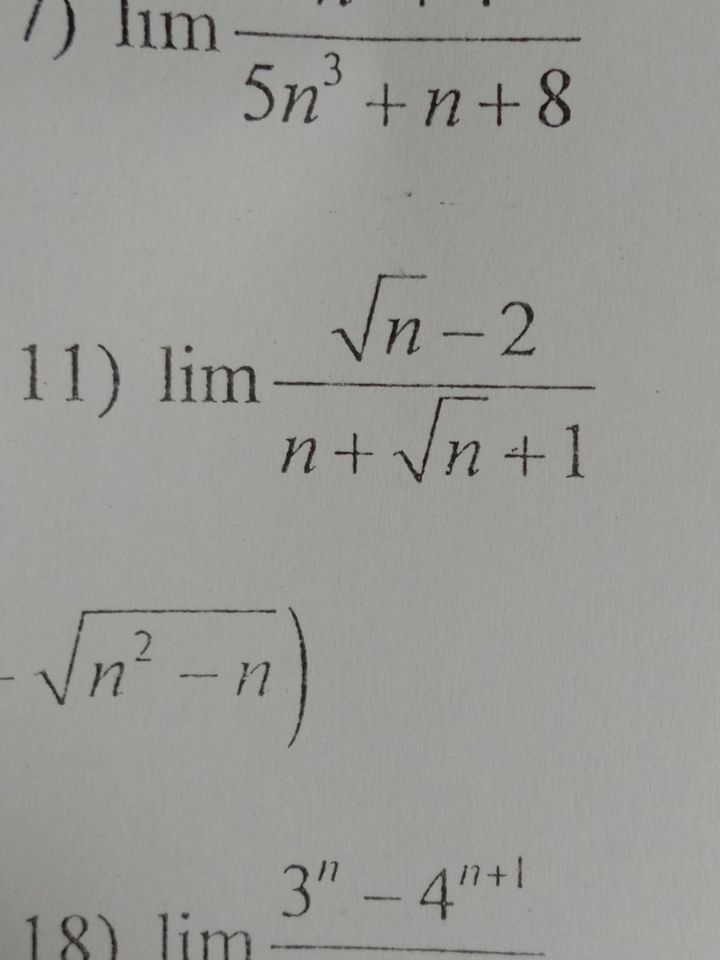 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 4.4 trang 156 SBT Toán 11
Bài tập 4.5 trang 156 SBT Toán 11
Bài tập 4.7 trang 157 SBT Toán 11
Bài tập 4.8 trang 157 SBT Toán 11
Bài tập 4.9 trang 157 SBT Toán 11
Bài tập 4.10 trang 157 SBT Toán 11
Bài tập 4.11 trang 157 SBT Toán 11
Bài tập 4.12 trang 157 SBT Toán 11
Bài tập 4.13 trang 157 SBT Toán 11
Bài tập 4.14 trang 157 SBT Toán 11
Bài tập 4.15 trang 157 SBT Toán 11
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





