Bài tập 3 trang 130 SGK Toán 11 NC
Chứng minh rằng các dãy số (un) sau đây có giới hạn 0:
a) \({u_n} = {\left( {0,99} \right)^n}\)
b) \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{2^n} + 1}}\)
c) \({u_n} = - \frac{{\sin \frac{{n\pi }}{5}}}{{{{\left( {1,01} \right)}^n}}}\)
Hướng dẫn giải chi tiết
a) Ta có \(\left| {0,99} \right| < 1 \Rightarrow \lim {u_n} = \lim {\left( {0,99} \right)^n} = 0\)
b) Ta có \(\left| {{u_n}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^n}}}{{{2^n} + 1}}} \right| = \frac{1}{{{2^n} + 1}} < {\left( {\frac{1}{2}} \right)^n}\)
và \(\lim {\left( {\frac{1}{2}} \right)^n} = 0 \Rightarrow \lim {u_n} = 0\)
c) Ta có
\(\begin{array}{l}
\left| {{u_n}} \right| = \left| { - \frac{{\sin \frac{{n\pi }}{5}}}{{{{\left( {1,01} \right)}^n}}}} \right| = \frac{{\left| {\sin \frac{{n\pi }}{5}} \right|}}{{{{\left( {1,01} \right)}^n}}} \le {\left( {\frac{1}{{1,01}}} \right)^n},\\
\lim {\left( {\frac{1}{{1,01}}} \right)^n} = 0 \Rightarrow \lim {u_n} = 0
\end{array}\)
-- Mod Toán 11 HỌC247
-


Tính lim (1-1/2^).(1-1/3^2)...(1-1/n^2)
bởi Tiêu Lương
 26/02/2020
Tính lim ý c
26/02/2020
Tính lim ý c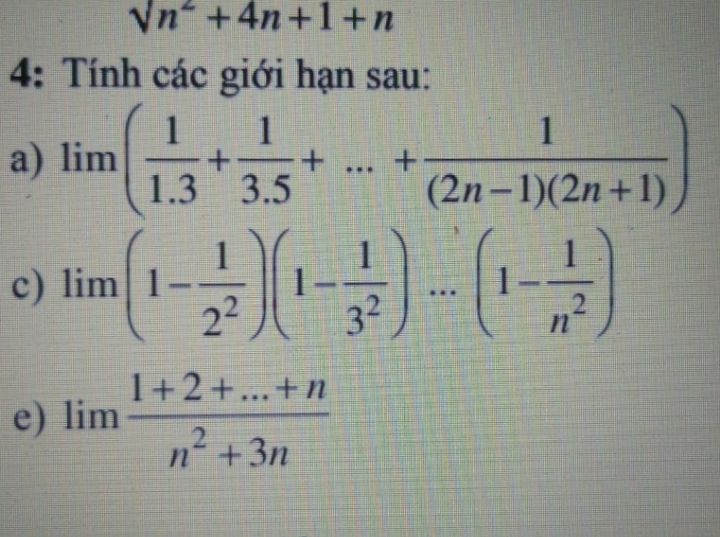 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm giới hạn lim n^4/((n+1)(2+n)(n^2+1))
bởi Nhi Nguyễn
 26/02/2020
26/02/2020
Tìm giới hạn của:
lim n4/((n+1)(2+n)(n2+1))
Giải chi tiết giúp mình với.
Theo dõi (0) 1 Trả lời -


Tìm giới hạn lim(2n+5)/(3n-3)
bởi Phương Thảo
 25/02/2020
Giúp tôi giải đáp
25/02/2020
Giúp tôi giải đáp Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giới hạn lim (3n+4)/(-2n+5)
bởi Tô Py
 24/02/2020
24/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính giới hạn L=lim(2019+2n^2)/(2020n^3+3n-1)
bởi Quốc Bảo
 22/02/2020
22/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





