Giải bài 4.14 tr 157 SBT Toán 11
\(\lim \frac{{{{\left( {2 - 3n} \right)}^2}\left( {n + 1} \right)}}{{1 - 4{n^3}}}\) bằng:
A. \(\frac{3}{4}\)
B. 0
C. \(\frac{9}{4}\)
D. \(-\frac{9}{4}\)
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
\lim \frac{{{{\left( {2 - 3n} \right)}^2}\left( {n + 1} \right)}}{{1 - 4{n^3}}} = \lim \frac{{{n^2}{{\left( {\frac{2}{n} - 3} \right)}^2}.n\left( {1 + \frac{1}{n}} \right)}}{{{n^3}\left( {\frac{1}{{{n^3}}} - 4} \right)}}\\
= \lim \frac{{{{\left( {2n - 3} \right)}^2}\left( {1 + \frac{1}{n}} \right)}}{{\frac{1}{{{n^3}}} - 4}} = \frac{{{{\left( { - 3} \right)}^2}}}{{ - 4}} = \frac{{ - 9}}{4}
\end{array}\)
Đáp án: D
-- Mod Toán 11 HỌC247
-

 giải giúp em bài này vs ạ
giải giúp em bài này vs ạ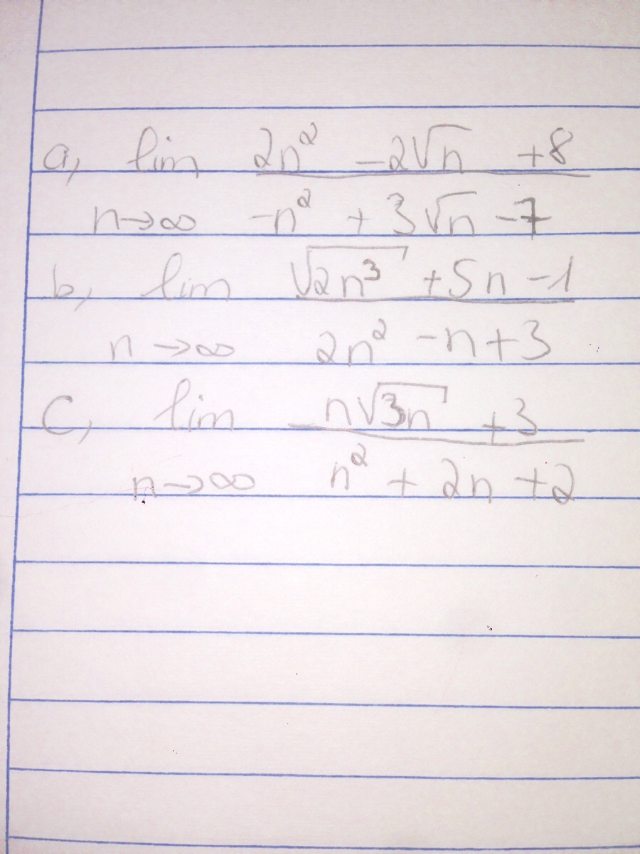 Theo dõi (1) 10 Trả lời
Theo dõi (1) 10 Trả lời -


Tính giới hạn dãy số 1/(căn(n+2)-căn(n+1))
bởi Thương Hoài
 01/04/2020
01/04/2020
 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tính giới hạn của (x-3)/√(x^2-9)
bởi My Duyen Nguyen Thi
 01/04/2020
Tính lim
01/04/2020
Tính lim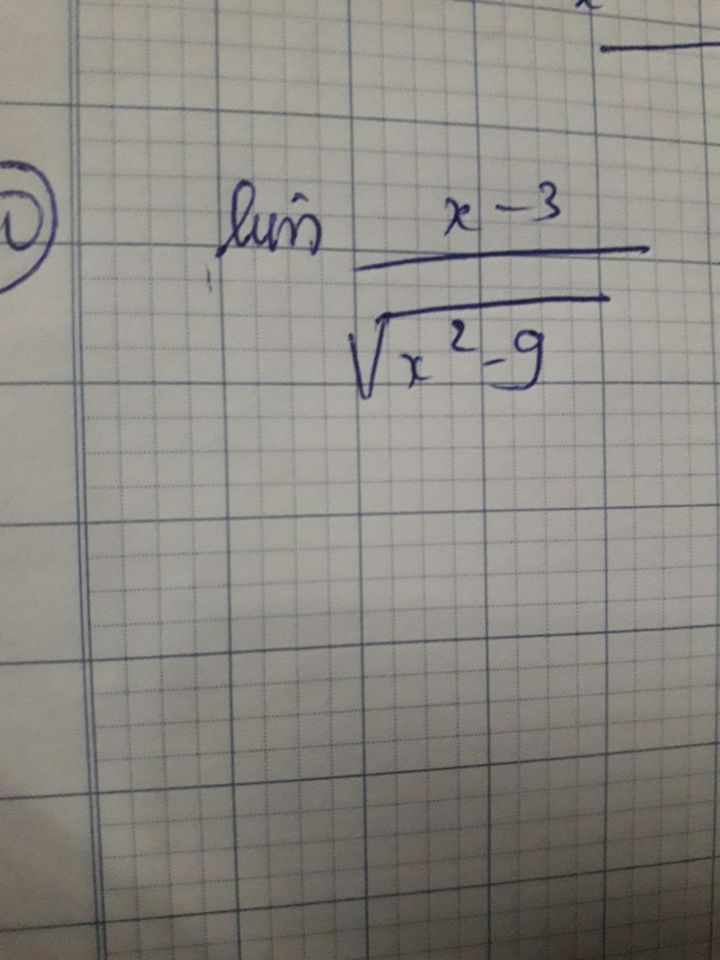 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tính giới hạn dãy số (5n+1)/(căn(4n^2-3n-2n)
bởi Duyên Mỹ
 31/03/2020
31/03/2020
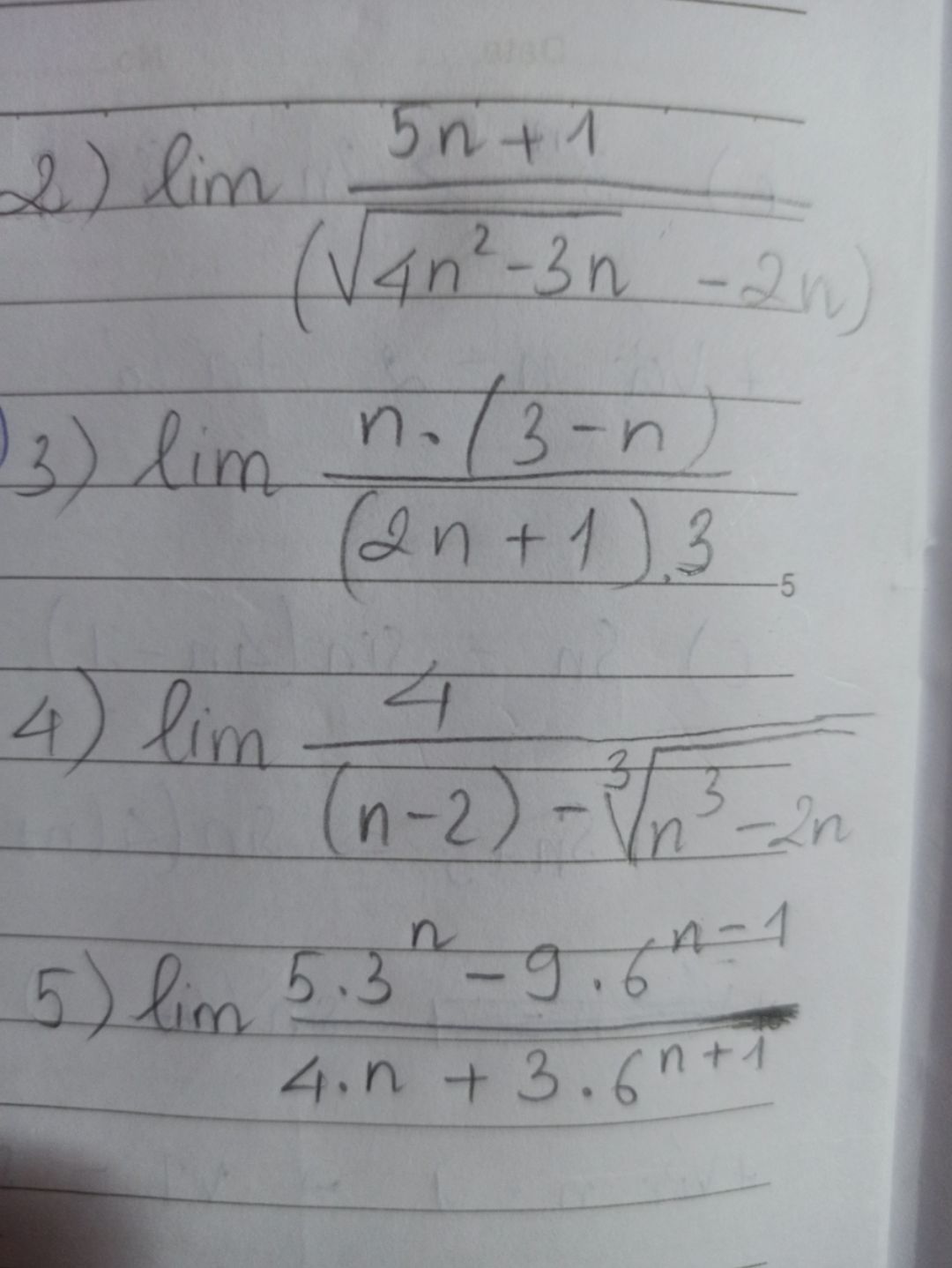 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Cho tam giác đều cạnh x. Ta lấy trung điểm của các cạnh tam giác đó vẽ tiếp tam giác đều thứ 2 và tiếp tục làm thế với tam giác mới. Tính giới hạn của tổng diện tích các tam giác liên tiếp đó khi x dẫn tới 3
bởi Linh Đàm
 31/03/2020
Cấp số nhân lùi vô hạnTheo dõi (0) 1 Trả lời
31/03/2020
Cấp số nhân lùi vô hạnTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.12 trang 157 SBT Toán 11
Bài tập 4.13 trang 157 SBT Toán 11
Bài tập 4.15 trang 157 SBT Toán 11
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





