Bài tập 8 trang 135 SGK Toán 11 NC
Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A1B1C1,…, tam giác An+1Bn+1Cn+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, … . Gọi p1, p2, ..., pn, … và S1, S2, …, Sn, … theo thứ tự là chu vi và diện tích của các tam giác.
a. Tìm giới hạn của các dãy số (pn) và (Sn).
b. Tìm các tổng p1+p2+...+pn+... và S1+S2+...+Sn+...
Hướng dẫn giải chi tiết
a) Ta có \({p_1} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{{3a}}{2};\)
\({p_2} = \frac{{3a}}{4} = \frac{{3a}}{{{2^2}}};...;{p_n} = \frac{{3a}}{{{2^n}}}\)
(chứng minh bằng qui nạp)
Vì \(\lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\) nên \(\lim {p_n} = 0\).
Ta có:
Diện tích tam giác ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)
Diện tích tam giác A1B1C1 là \({S_1} = \frac{S}{4}\)
Bằng phương pháp qui nạp, ta chứng minh được rằng diện tích tam giác AnBnCn là \({S_n} = \frac{{{a^2}\sqrt 3 }}{4}.{\left( {\frac{1}{4}} \right)^n}\)
Vì \(\lim {\left( {\frac{1}{4}} \right)^n} = 0\) nên \(\lim {S_n} = 0\).
b) Ta có (pn) là cấp số nhân lùi vô hạn có công bội \(q = \frac{1}{2}\), do đó:
\({p_1} + {p_2} + ... + {p_n} + ... = \frac{{{p_1}}}{{1 - \frac{1}{2}}} = 2{p_1} = 3a\)
(Sn) là cấp số nhân lùi vô hạn có công bội \(q' = \frac{1}{4}\) do đó:
\({S_1} + {S_2} + ... + {S_n} + ... = \frac{{{S_1}}}{{1 - \frac{1}{4}}} = \frac{4}{3}{S_1} = \frac{S}{3} = \frac{{{a^2}\sqrt 3 }}{{12}}\)
-- Mod Toán 11 HỌC247
-


Tính lim (3n^2-1).(-2n^3-3)^4/(-2n^4-1)^3
bởi nguyễn minh cường
 13/02/2020
Câu 5
13/02/2020
Câu 5 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính lim căn(2n^4-n+3)
bởi Bach Hoai Diem Nguyen
 13/02/2020
Tìm lim
13/02/2020
Tìm lim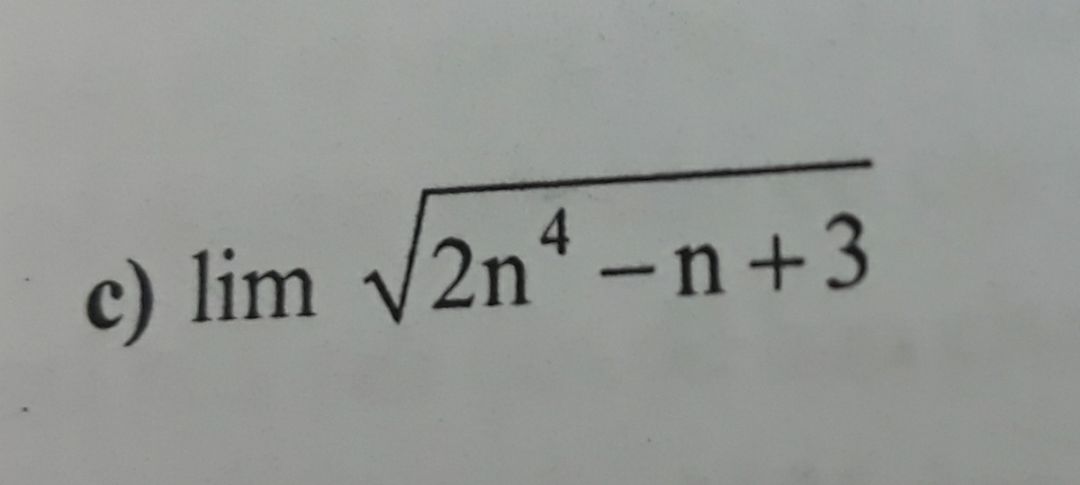 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm giới hạn lim (2n^3-5n^2+1)/(n^2-1)
bởi Trang Trần Thị Thùy
 13/02/2020
Giúp với ạ
13/02/2020
Giúp với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính lim -7/(2n^2-n+5)
bởi Vy Lê Thảo
 12/02/2020
12/02/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tính lim n.căn(n+2)/(n^2+n.căn(2n+13))
bởi Thùy Linh
 12/02/2020
Câu c ạ
12/02/2020
Câu c ạ Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





