Bài tập 1 trang 130 SGK Toán 11 NC
Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0:
a) \(\frac{{{{\left( { - 1} \right)}^n}}}{{n + 5}}\)
b) \(\frac{{\sin n}}{{n + 5}}\)
c) \(\frac{{\cos 2n}}{{\sqrt n + 1}}\)
Hướng dẫn giải chi tiết
a) Ta có \(\left| {\frac{{{{\left( { - 1} \right)}^n}}}{{n + 5}}} \right| = \frac{1}{{n + 5}} < \frac{1}{n}\) và \(\lim \frac{1}{n} = 0 \Rightarrow \lim \frac{{{{\left( { - 1} \right)}^n}}}{{n + 5}} = 0\)
b) Ta có \(\left| {\frac{{\sin n}}{{n + 5}}} \right| \le \frac{1}{{n + 5}} < \frac{1}{n}\) và \(\lim \frac{1}{n} = 0 \Rightarrow \lim \frac{{\sin n}}{{n + 5}} = 0\)
c) Ta có \(\left| {\frac{{\cos 2n}}{{\sqrt n + 1}}} \right| \le \frac{1}{{\sqrt n + 1}} < \frac{1}{{\sqrt n }}\) và \(\lim \frac{1}{{\sqrt n }} = 0 \Rightarrow \lim \frac{{\cos 2n}}{{\sqrt n + 1}} = 0\)
-- Mod Toán 11 HỌC247
-


Tính giới hạn lim (∛(n^3+1)+n)/√(n^2+n+1)
bởi Thảo Ngân
 02/03/2020
02/03/2020
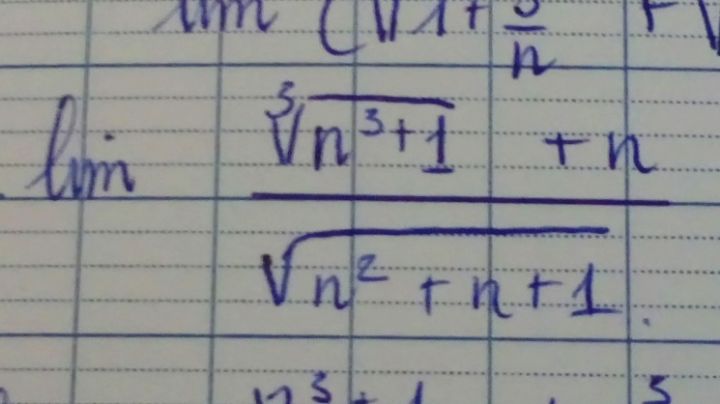 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính giới hạn ∛(n+1)-∛n
bởi Nguyễn Hoàng Minh
 01/03/2020
Giúp với ạ
01/03/2020
Giúp với ạ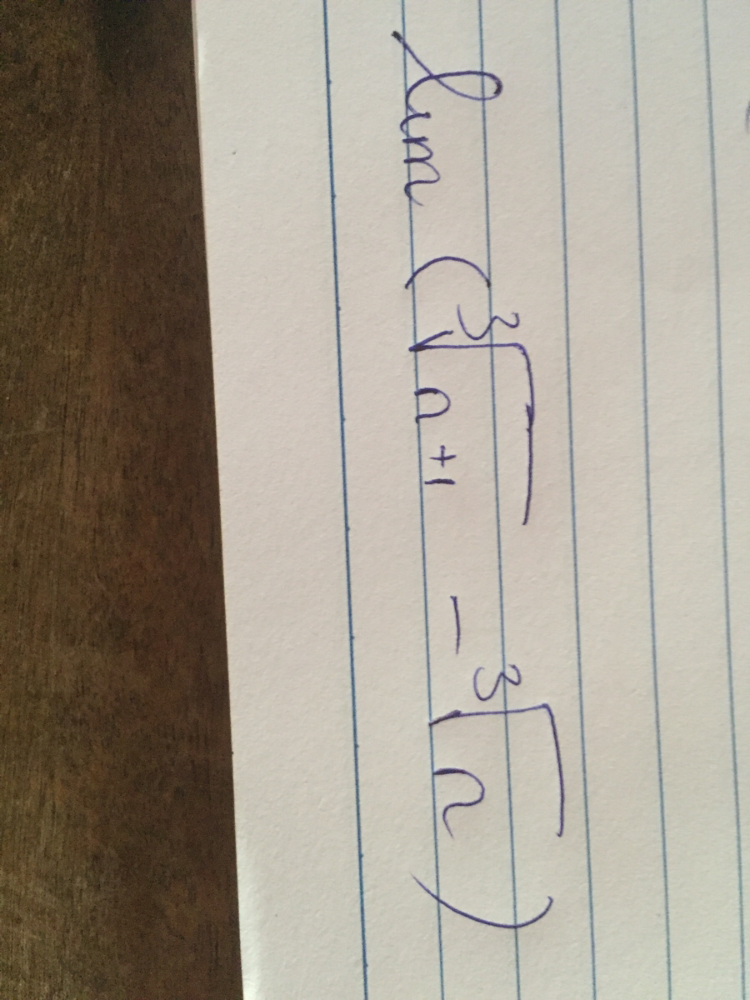 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim (n^2-14n-7)
bởi Tuyết Hà
 29/02/2020
29/02/2020
 Theo dõi (2) 5 Trả lời
Theo dõi (2) 5 Trả lời -


Tính lim căn (n^2+2n-2n)/3n-2
bởi huỳnh văn hoài nam
 28/02/2020
Câu này giải làm sao vậy
28/02/2020
Câu này giải làm sao vậy Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giới hạn lim(3^n+2.5^n)/(6.5^n-2.4^n)
bởi huỳnh văn hoài nam
 28/02/2020
Câu 8 lam sao vay
28/02/2020
Câu 8 lam sao vay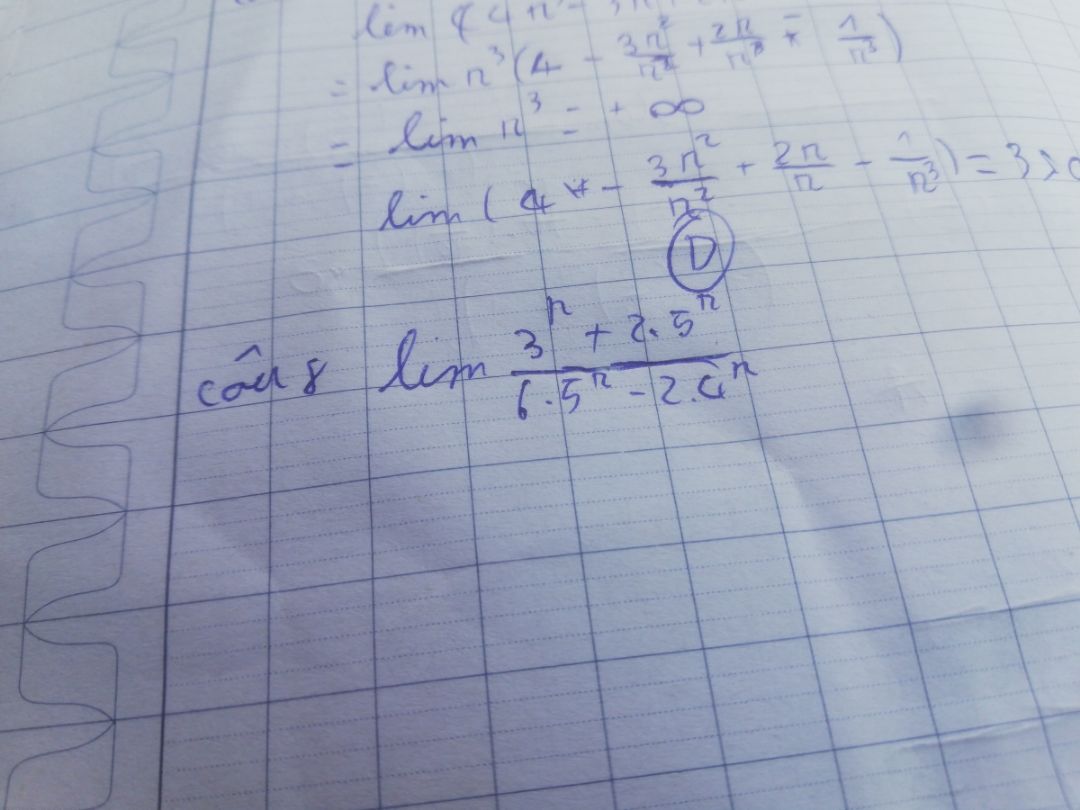 Theo dõi (0) 17 Trả lời
Theo dõi (0) 17 Trả lời
Bài tập SGK khác
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





