Bài tập 15 trang 142 SGK Toán 11 NC
Tìm giới hạn của các dãy số (un) với:
a) \({u_n} = \frac{{{3^n} + 1}}{{{2^n} - 1}}\)
b) \({u_n} = {2^n} - {3^n}\)
Hướng dẫn giải chi tiết
Chia cả tử và mẫu cho 3n ta được:
\({u_n} = \frac{{1 + {{\left( {\frac{1}{3}} \right)}^n}}}{{{{\left( {\frac{2}{3}} \right)}^n} - {{\left( {\frac{1}{3}} \right)}^n}}}\)
Vì \(\lim \left[ {1 + {{\left( {\frac{1}{3}} \right)}^n}} \right] = 1 > 0,lim\left[ {{{\left( {\frac{2}{3}} \right)}^n} - {{\left( {\frac{1}{3}} \right)}^n}} \right] = 0\) nên \(\lim {u_n} = + \infty \)
b) Ta có \({u_n} = {3^n}\left[ {{{\left( {\frac{2}{3}} \right)}^n} - 1} \right]\)
Vì \(\lim {3^n} = + \infty ,\lim \left[ {{{\left( {\frac{2}{3}} \right)}^n} - 1} \right] = - 1 < 0\) nên \(\lim {u_n} = - \infty \)
-- Mod Toán 11 HỌC247
-


Tính lim (2n-3n^3+1)/(n^3+n^2)
bởi lan ngọc
 07/01/2020
07/01/2020
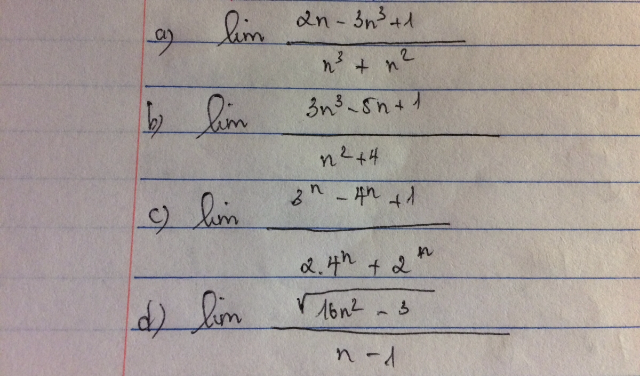 Theo dõi (2) 11 Trả lời
Theo dõi (2) 11 Trả lời -


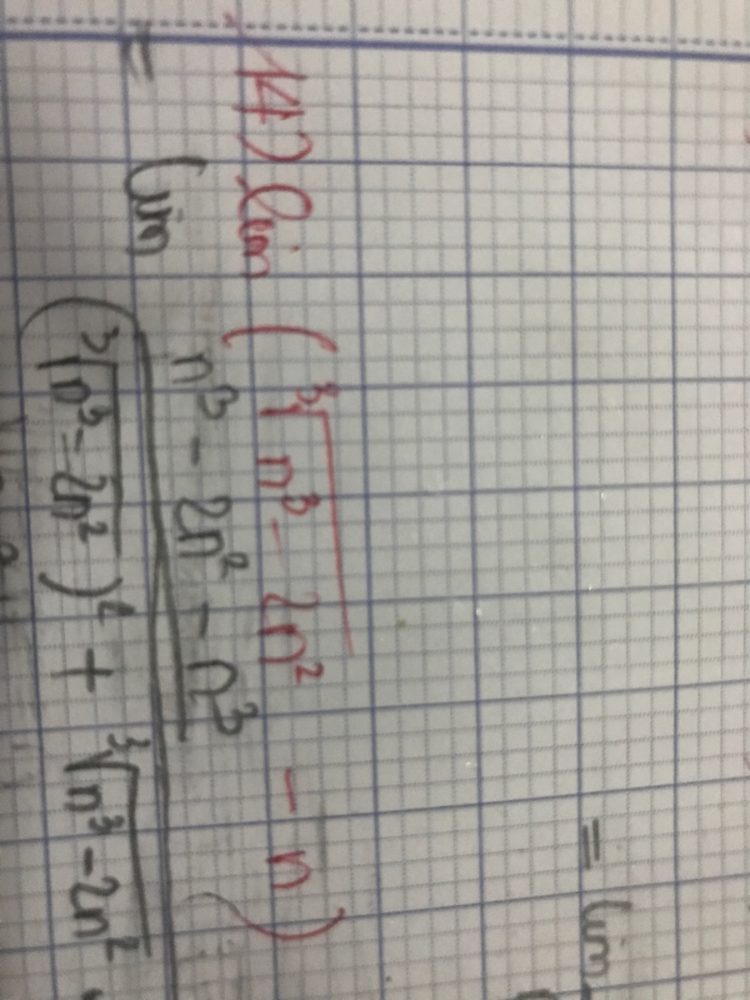
Tính lim(căn bậc 3(n^3-2n^2)-n)
bởi Ngọc Tuyền
 06/01/2020
06/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giới hạn (3n^2-1).(n^2+2)/(1^3+2^3+...+n^3)
bởi Hương Hoài
 31/12/2019
31/12/2019
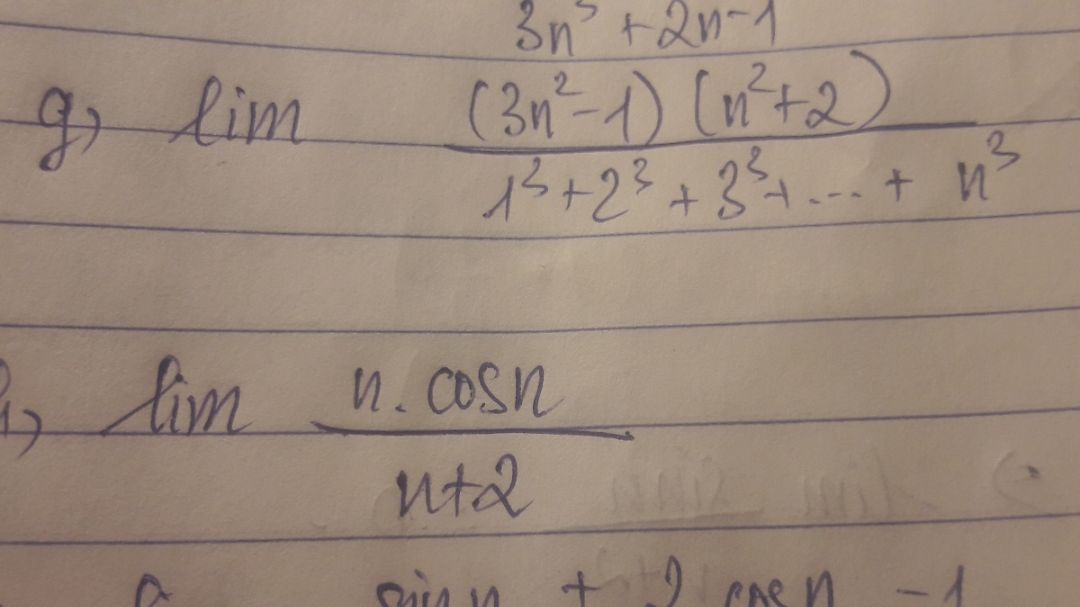 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim(sin2x-sin5x)/(sin2x+sin3x) khi x tiến tới 0
bởi Tyyu Zheng
 27/12/2019
27/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim 3n^4 2^3-n^2/4n^3-n-1
bởi Hong Anh Nguyen
 12/12/2019
12/12/2019
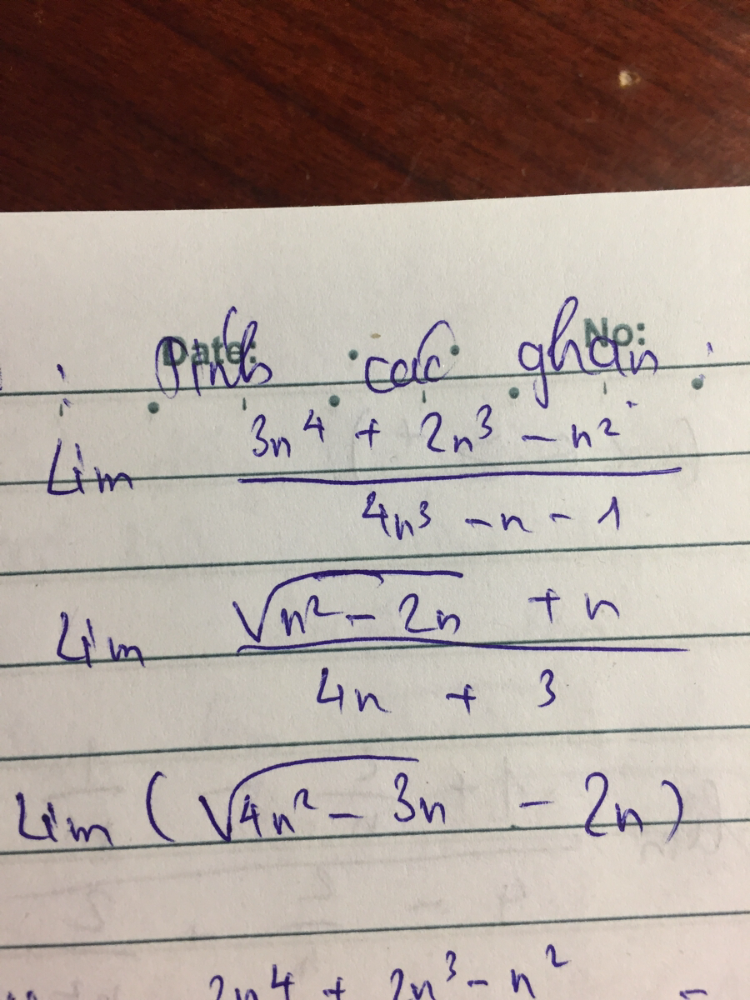 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời





