Giải bài 4.11 tr 157 SBT Toán 11
Cho dãy số () có số hạng tổng quát là \({b_n} = \sin \alpha + {\sin ^2}\alpha + ... + {\sin ^n}\alpha \) với \(\alpha \ne \frac{\pi }{2} + k\pi \). Tìm giới hạn của ().
Hướng dẫn giải chi tiết
Xét dãy số: \(\sin \alpha ,{\sin ^2}\alpha ,{\sin ^3}\alpha ,...,{\sin ^n}\alpha \) với \(\alpha \ne \frac{\pi }{2} + k\pi \) là cấp số nhân có công bội là \(\sin \alpha \).
Vì \(\left| {\sin \alpha } \right| < 1\) với \(\alpha \ne \frac{\pi }{2} + k\pi \) nên \(\left( {{{\sin }^n}\alpha } \right)\) là cấp số nhân lùi vô hạn.
Do đó ta có: \(\lim {b_n} = \lim (\sin \alpha + {\sin ^2}\alpha + {\sin ^3}\alpha + ... + {\sin ^n}\alpha + ...) = \frac{{\sin \alpha }}{{1 - \sin \alpha }}\)
-- Mod Toán 11 HỌC247
-


Chọn khẳng định sai?
bởi Mây Mây
 30/04/2020
30/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


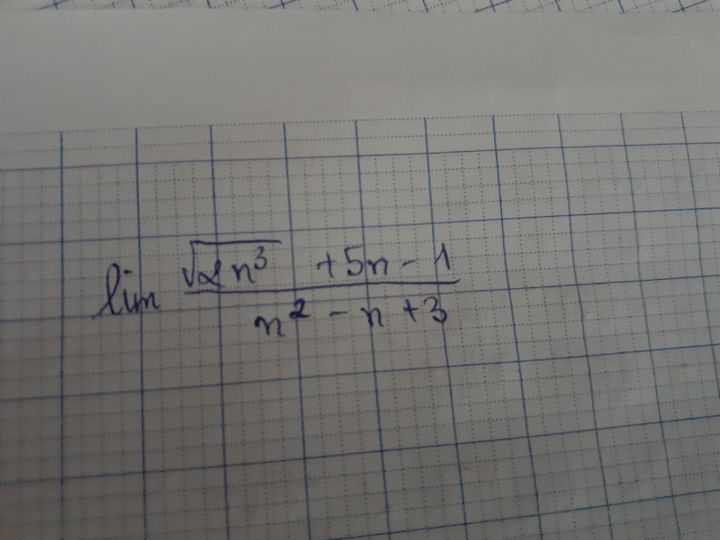 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {{x^2} + 3x} - 1}}{{x - 1}}\)?
bởi Quân Trần
 22/04/2020
22/04/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm giới hạn dãy số (căn 16n^2-5n^2+1-4n)
bởi Đào Thị Hồng Nhung
 21/04/2020
Tìm giới hạn của dãy sốTheo dõi (0) 0 Trả lời
21/04/2020
Tìm giới hạn của dãy sốTheo dõi (0) 0 Trả lời -


Tìm giới hạn lim 2x3^n+4^n/2^n+7^n
bởi Bảo Nguyễn
 17/04/2020
17/04/2020
lim 2x3^n+4^n/2^n+7^n
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 4.9 trang 157 SBT Toán 11
Bài tập 4.10 trang 157 SBT Toán 11
Bài tập 4.12 trang 157 SBT Toán 11
Bài tập 4.13 trang 157 SBT Toán 11
Bài tập 4.14 trang 157 SBT Toán 11
Bài tập 4.15 trang 157 SBT Toán 11
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





