Bài tập 11 trang 142 SGK Toán 11 NC

Lý thuyết10 Trắc nghiệm

45 BT SGK

212 FAQ

Tìm giới hạn của các dãy số (u_n) với:

a) \({u_n} = - 2{n^3} + 3n + 5\)

b) \({u_n} = \sqrt {3{n^4} + 5{n^3} - 7n} \)

Toán 11 Chương 4 Bài 1 Trắc nghiệm Toán 11 Chương 4 Bài 1 Giải bài tập Toán 11 Chương 4 Bài 1

Hướng dẫn giải chi tiết

a) Ta có \({u_n} = {n^3}\left( { - 2 + \frac{3}{{{n^2}}} + \frac{5}{{{n^3}}}} \right)\)

Vì \(\lim {n^3} = + \infty \) và \(\lim \left( { - 2 + \frac{3}{{{n^2}}} + \frac{5}{{{n^3}}}} \right) = - 2 < 0\) nên \(\lim {u_n} = - \infty \)

b) Ta có \({u_n} = {n^2}\sqrt {3 + \frac{5}{n} - \frac{7}{{{n^3}}}} \)

Vì \(\lim {n^2} = + \infty \) và \(\lim \sqrt {3 + \frac{5}{n} - \frac{7}{{{n^3}}}} = \sqrt 3 > 0\) nên \(\lim {u_n} = + \infty \)

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 11 trang 142 SGK Toán 11 NC HAY thì click chia sẻ

YOMEDIA

Dãy nào sau đây có giới hạn khác 0?

bởi Hương Mai 06/02/2020

Theo dõi (1) 2 Trả lời
Tìm L=lim(-3n^3+2n^2-5)

bởi Hương Mai 05/02/2020

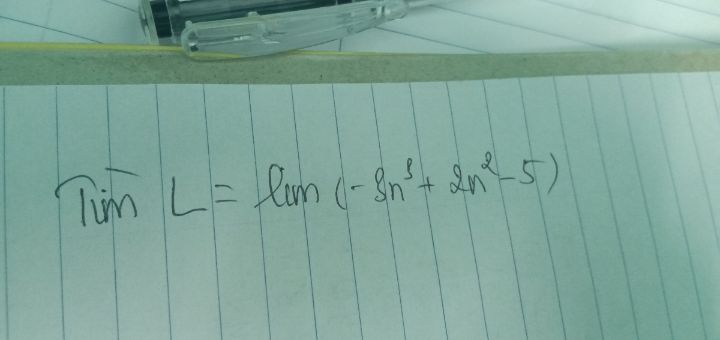Theo dõi (1) 10 Trả lời
Tính giới hạn lim(n+1)/(n-2)

bởi Bùi Thị Thảo 03/02/2020

Giải hộ em với ạ❤

Theo dõi (1) 0 Trả lời
Giá trị đúng của lim Vn(n+1-In-1) là?

bởi Trịnh Huyền 03/02/2020

Câu 313. Giá trị đúng của lim Vn(n+1-In-1) là: A.-1. B. 0. D. +o. C. 1.

Câu 314. Cho dãy số (un) với un = (n-1), 2n +2 . Chọn kết quả đúng của limu, là: %3D n' +n? -1 A. -00. B. 0. D. +oo, C. 1. 5" -1

Câu 315. lim- bằng : 3" +1 A. +oo. D. -co. B. 1. C. 0. 10

Câu 316. lim bằng : Vn* +n? +1 C. 0. D. -00. A. +oo. B. 10.

Câu 317. lim200 - 3n +2n² bằng : C too. D. -0. B. 1. A. 0. Tìm két quả đúng của limu, .

Câu 318. Cho dãy số có giới hạn (un) xác định bởi : -,n 21 2-u C. -1. D. B. 1. A. 0. 1 1 1 [2

Câu 319. Tìm giá trị đúng của S = 2| 1+-+ 2 48 2" C. 2 2. D. B. 2. A. 2 +1. 4" +2"+1 bằng : C

âu 320. Lim4 3" + 4"+2 1 B. D. +oo. A. 0. In+1-4

Câu 321. Tính giới hạn: lim Vn+1+n C.-1. D. B.O. A. 1. +(2n +1)- * 3n +4 1+3+5+...+ 3n 14,

Câu 322. Tính giới hạn: lim C. 2 3 B. D. 1. A. 0. 1 nlat1) +......+

Câu 323. Tính giới hạn: lim n(n+1) 1.2 2.3 3 C. 21 D. Không có giới hạn. B. 1. A. 0.

Theo dõi (0) 0 Trả lời
Tính lim (-n^4-2n^2+4)

bởi Vũ Thị Thanh 28/01/2020

Theo dõi (0) 4 Trả lời