Bài tập 16 trang 143 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}}\)
b) \(\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}}\)
c) \(\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}}\)
d) \(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}} = \lim \frac{{{n^3}\left( {\frac{1}{n} + \frac{4}{{{n^2}}} - \frac{5}{{{n^3}}}} \right)}}{{{n^3}\left( {3 + \frac{1}{n} + \frac{7}{{{n^3}}}} \right)}}\\
= \lim \frac{{\frac{1}{n} + \frac{4}{{{n^2}}} - \frac{5}{{{n^3}}}}}{{3 + \frac{1}{n} + \frac{7}{{{n^3}}}}} = \frac{0}{3} = 0
\end{array}\)
b)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}}\\
= \lim {n^2}.\frac{{{n^3}\left( {1 + \frac{1}{n} - \frac{3}{{{n^4}}} - \frac{2}{{{n^5}}}} \right)}}{{{n^3}\left( {4 + \frac{6}{n} + \frac{9}{{{n^3}}}} \right)}}
\end{array}\\
{ = \lim {n^2}.\frac{{\left( {1 + \frac{1}{n} - \frac{3}{{{n^4}}} - \frac{2}{{{n^5}}}} \right)}}{{\left( {4 + \frac{6}{n} + \frac{9}{{{n^3}}}} \right)}} = + \infty }
\end{array}\)
c)
\(\begin{array}{l}
\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}} = \lim \frac{{{n^2}\sqrt {2 + \frac{3}{{{n^3}}} - \frac{2}{{{n^4}}}} }}{{{n^2}\left( {2 - \frac{1}{n} + \frac{3}{{{n^2}}}} \right)}}\\
= \lim \frac{{\sqrt {2 + \frac{3}{{{n^3}}} - \frac{2}{{{n^4}}}} }}{{2 - \frac{1}{n} + \frac{3}{{{n^2}}}}} = \frac{{\sqrt 2 }}{2}
\end{array}\)
d)
\(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}} = \lim \frac{{{{\left( {\frac{3}{5}} \right)}^n} - 2}}{{7.{{\left( {\frac{1}{5}} \right)}^n} + 3}} = - \frac{2}{3}\)
(vì \(\lim {\left( {\frac{3}{5}} \right)^n} = \lim {\left( {\frac{1}{5}} \right)^n} = 0\))
-- Mod Toán 11 HỌC247
-


Tính giới hạn lim(n căn n-2 căn(n+1))
bởi Nguyễn Thu Trang
 04/12/2019
Tính giới hạn sau
04/12/2019
Tính giới hạn sau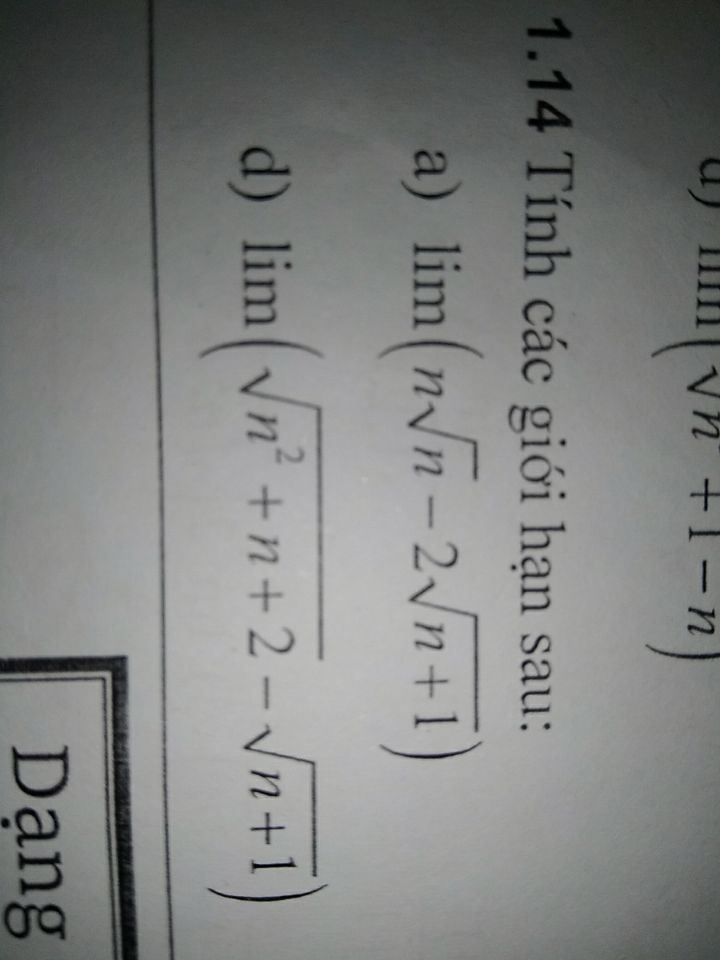 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giới hạn của lim (căn bậc 4 của (n^4 cộng 1) - n)
bởi Thanh Tuyền
 11/01/2019
11/01/2019
lim ( (căn bậc 4 của (n (mũ 4) cộng 1)) - n)
Theo dõi (0) 2 Trả lời -


tìm giới hạn:
lim 4n5-3n4-2n3+7n-9/-5n(3n2-2n+1)(5-2n2)
Theo dõi (0) 1 Trả lời -


Tính lim 1/(căn(3n+2)-căn(2n+1))
bởi thủy tiên
 24/10/2018
24/10/2018
tìm giới hạn sau : lim\(\frac{1}{\sqrt{3n+2}-\sqrt{2n+1}}\)
mong các bn và các thầy cô giúp với ạ
Theo dõi (0) 1 Trả lời -


Bài 1.15 trang 155 sách bài tập Đại số 11
bởi Tay Thu
 24/10/2018
Bài 1.15 (Sách bài tập trang 155)
24/10/2018
Bài 1.15 (Sách bài tập trang 155)Cho số thập phân vô hạn tuần hoàn \(a=34,121212....\) (chu kì là 12). Hãy viết a dưới dạng một phân số ?
Theo dõi (0) 1 Trả lời





