Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 17665
Cho hàm số \(y = \frac{{x + 3}}{{x + 2}}.\) Khẳng định nào sau đây là khẳng định đúng:
- A. Hàm số đồng biến trên \(\mathbb{R}.\)
- B. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right).\)
- C. Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 2 \right\}.\)
- D. Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right).\)
-
Câu 2: Mã câu hỏi: 17666
Hai điểm cực trị của hàm số \(y = {x^3} + 3{x^2} - 4\) đối xứng nhau qua đường thẳng:
- A. y=x-1.
- B. y=2x-1.
- C. 3x-6y-13=0.
- D. x-2y-3=0.
-
Câu 3: Mã câu hỏi: 17667
Cho hình chóp S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’ sao cho \(SA' = \frac{2}{3}SA,SB' = \frac{5}{6}SB,SC' = \frac{k}{{k + 1}}SC.\) Biết rằng \({V_{S.A'B'C'}} = \frac{1}{2}{V_{S.ABC}}.\) Lựa chọn phương án đúng.
- A. k=6.
- B. k=7.
- C. k=8.
- D. k=9.
-
Câu 4: Mã câu hỏi: 17668
Cho \(\left( {{C_m}} \right):f(x) = {x^4} + 2m{x^2} + m.\) Tìm m để \(({C_m})\) có ba cực trị.
- A. m<0.
- B. m=0.
- C. m>0.
- D. \(m \ge 0.\)
-
Câu 5: Mã câu hỏi: 17669
Đồ thị hàm số \(y = \frac{1}{{3x + 2}}\) có bao nhiêu đường tiệm cận?
- A. 3.
- B. 1.
- C. 4.
- D. 2.
-
Câu 6: Mã câu hỏi: 17670
Giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\) trên khoảng \((1; + \infty )\) là:
- A. \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = 3.\)
- B. \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = - 1.\)
- C. \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = 5.\)
- D. \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = - \frac{7}{3}.\)
-
Câu 7: Mã câu hỏi: 17671
Hàm số \(y = - \frac{1}{3}{x^3} - (m + 1){x^2} + (m + 1)x + 1\) nghịch biến trên tập xác định của nó khi:
- A. \( - 2 < m < - 1\)
- B. \(m < - 2\)
- C. \(m > - 1\)
- D. \( - 2 \le m \le - 1.\)
-
Câu 8: Mã câu hỏi: 17672
Tìm giá trị lớn nhất của hàm số \(f(x) = {x^3} - 8{x^2} + 16x - 9\) trên đoạn [1;3].
- A. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f(x) = - 6.\)
- B. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f(x) = \frac{{13}}{{27}}.\)
- C. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f(x) = 0.\)
- D. \(\mathop {\max }\limits_{\left[ {1;3} \right]} f(x) = 5.\)
-
Câu 9: Mã câu hỏi: 17673
Đồ thị hàm số nào sau đây không có tiệm cận ngang?
- A. \(y = \frac{{2x - 3}}{{x + 1}}.\)
- B. \(y = \frac{{\sqrt {{x^4} + 3{x^2} + 7} }}{{2x - 1}}.\)
- C. \(y = \frac{3}{{x - 2}} + 1.\)
- D. \(y = \frac{3}{{{x^2} - 1}}.\)
-
Câu 10: Mã câu hỏi: 17674
Đồ thị hàm số \(y = {x^3} - 3x\) có điểm cực đại là:
- A. \(( - 1;2).\)
- B. \((1; - 2).\)
- C. \((1;0).\)
- D. \(( - 1;0).\)
-
Câu 11: Mã câu hỏi: 17722
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = x + 1 + \sqrt {4 - {x^2}} \) lần lượt là M và m, chọn câu trả lời đúng.
- A. \(M = \sqrt 2 + 1;\,m = - 1.\)
- B. \(M = 2\sqrt 2 + 1;\,m = 1.\)
- C. \(M = 2\sqrt 2 + 1;\,m = - 1.\)
- D. \(M = 3;\,m = 1.\)
-
Câu 12: Mã câu hỏi: 17723
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số dược liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
- A. \(y = - {x^3} + 3{x^2} + 1\)
- B. \(y = {x^3} - 3{x^2} + 3x + 1.\)
- C. \(y = - {x^3} - 3{x^2} - 1.\)
- D. \(y = {x^3} - 3x + 1.\)
-
Câu 13: Mã câu hỏi: 17724
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình bên dưới đây.Hỏi đồ thị hàm số \(y = f(x)\) có bao nhiêu đường tiệm cận?
- A. 4
- B. 1
- C. 3
- D. 2
-
Câu 14: Mã câu hỏi: 17725
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC vuông tại A, AB=3a, AC=4a, SA=4a. Tính thể tích khối chóp S.ABC.
- A. \(2{a^3}.\)
- B. \(6{a^3}.\)
- C. \(8{a^3}.\)
- D. \(9{a^3}.\)
-
Câu 15: Mã câu hỏi: 17726
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA’=4A’M, BB’=4B’N. Mặt phẳng (C’MN) chia khối lăng trụ thành hai phần. Gọi \({V_1}\) là thể tích khối chóp C’.A’B’MN và \({V_2}\) là thể tích khối đa diện ABCMNC’. Tính tỷ số \(\frac{{{V_1}}}{{{V_2}}}.\)
- A. \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{5}.\)
- B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{4}{5}.\)
- C. \(\frac{{{V_1}}}{{{V_2}}} = \frac{2}{5}.\)
- D. \(\frac{{{V_1}}}{{{V_2}}} = \frac{3}{5}.\)
-
Câu 16: Mã câu hỏi: 18049
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc \({45^0}.\) Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
- A. \(\frac{{{a^3}\sqrt 3 }}{{10}}.\)
- B. \(\frac{{{a^3}\sqrt 3 }}{{12}}.\)
- C. \(\frac{{{a^3}}}{4}.\)
- D. \(\frac{{{a^3}}}{8}.\)
-
Câu 17: Mã câu hỏi: 18051
Tìm giá trị nhỏ nhất của hàm số \(y = 3 + \sqrt {{x^2} - 2x + 5} .\)
- A. \(\mathop {\min y}\limits_\mathbb{R} = 0.\)
- B. \(\mathop {\min y}\limits_\mathbb{R} = 3.\)
- C. \(\mathop {\min y}\limits_\mathbb{R} = 3 + \sqrt 5 .\)
- D. \(\mathop {\min y}\limits_\mathbb{R} = 5.\)
-
Câu 18: Mã câu hỏi: 18052
Tìm m để hàm số \(y = 2{x^3} + 3(m - 1){x^2} + 6(m - 2) + 3\) nghịch biến trên một khoảng có độ dài lớn hơn 3.
- A. m>6
- B. \(m \in \left( {0;6} \right)\)
- C. m<0
- D. m<0 hoặc m>6.
-
Câu 19: Mã câu hỏi: 18056
Hình sau đây là đồ thị của hàm số \(y = a{x^3} + b{x^2} + cx + d.\)
Khẳng định nào dưới đây đúng?
- A. \(a < 0,b > 0,c < 0,d < 0.\)
- B. \(a < 0,b < 0,c > 0,d < 0.\)
- C. \(a < 0,b > 0,c > 0,d < 0.\)
- D. \(a > 0,b > 0,c > 0,d < 0.\)
-
Câu 20: Mã câu hỏi: 18060
Khoảng đồng biến của hàm số \(y = - {x^3} + 3x - 4\) là:
- A. (0;1)
- B. (0;2)
- C. \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\)
- D. (-1;1)
-
Câu 21: Mã câu hỏi: 18066
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết rằng mặt phẳng (SBC) tạo với mặt phẳng đáy một góc \({30^0}.\)
- A. \(\frac{{2\sqrt 3 {a^3}}}{3}.\)
- B. \(\frac{{4\sqrt 3 {a^3}}}{3}.\)
- C. \(\frac{{\sqrt 3 {a^3}}}{2}.\)
- D. \(2\sqrt 3 {a^3}.\)
-
Câu 22: Mã câu hỏi: 18069
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
- A. ab<0,bc>0,cd>0.
- B. ab<0,bc>0,cd<0.
- C. ab>0,bc>0,cd<0.
- D. ab<0,bc<0,cd<0.
-
Câu 23: Mã câu hỏi: 18071
Hàm số \(y = {x^3} + 3{x^2} - 9x + 4\) nghịch biến trên:
- A. \(\left( { - 3; + \infty } \right)\)
- B. \(\left( { - \infty ;1} \right)\)
- C. \(\left( { - 3;1} \right)\)
- D. \(\left( { - \infty ; - 3} \right);\left( {1; + \infty } \right)\)
-
Câu 24: Mã câu hỏi: 18073
Cho hình chóp tam giác đề S.ABC có cạnh đáy bằng \(a\sqrt 2 ,\) góc giữa cạnh bên và đáy bằng \({45^0}.\) Thể tích khối chóp S.ABC là:
- A. \(\frac{{{a^3}}}{6}.\)
- B. \(\frac{{{a^3}\sqrt 2 }}{6}.\)
- C. \(\frac{{2{a^3}\sqrt 3 }}{9}.\)
- D. \(\frac{{{a^3}\sqrt 3 }}{{12}}.\)
-
Câu 25: Mã câu hỏi: 18075
Đường cong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?
- A. \(y = {x^3} - 3x\)
- B. \(y = {x^4} - {x^2} + 1\)
- C. \(y = - {x^3} + 3x - 1\)
- D. \(y = - {x^3} + 3x\)
-
Câu 26: Mã câu hỏi: 18137
Hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3{x^2} - 2\) đối xứng nhau qua đường thẳng:
- A. \(y = x + 1\)
- B. \(x - 2y + 1 = 0\)
- C. \(x + 2y - 2 = 0\)
- D. \(2x - 4y - 1 = 0\)
-
Câu 27: Mã câu hỏi: 18139
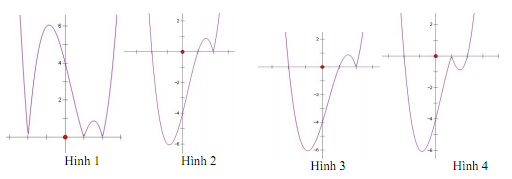
Cho hàm số \(y = (x - 1)({x^2} - 4)\) có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số \(y = \left| {x - 1} \right|({x^2} - 4)\) là hình nào dưới đây?
- A. Hình 1
- B. Hình 2
- C. Hình 3
- D. Hình 4
-
Câu 28: Mã câu hỏi: 18142
Tìm m để hàm số \(y = \frac{{mx - 2}}{{m - 2x}}\) nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right).\)
- A. \( - 2 < m \le 1\)
- B. \( - 2 < m < 2\)
- C. \( - 2 \le m \le 2\)
- D. m>2
-
Câu 29: Mã câu hỏi: 18148
Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu của A’ trên (ABC) trùng với tâm O của tam giác ABC. Biết A’O=a. Tính khoảng cách từ B’ đến mặt phẳng (A’BC).
- A. \(\frac{{3a}}{{\sqrt {21} }}\)
- B. \(\frac{{3a}}{4}\)
- C. \(\frac{{3a}}{{\sqrt {13} }}\)
- D. \(\frac{{3a}}{{\sqrt {28} }}\)
-
Câu 30: Mã câu hỏi: 18151
Đồ thị \((C):y = - {x^4} + 2{x^2}\) có 3 điểm cực trị tạo thành một tam giác. Chu vi tam giác đó là:
- A. \(2 + 2\sqrt 2 \)
- B. \(1 + \sqrt 2 \)
- C. \(\sqrt 2 \)
- D. \(3\)
-
Câu 31: Mã câu hỏi: 18153
Đồ thị hàm số \(y = {(x + 1)^2}({x^2} - 2x + 2)\) và trục hoành có tất cả bao nhiêu điểm chung?
- A. 1
- B. 2
- C. 3
- D. 4
-
Câu 32: Mã câu hỏi: 18154
Cho đồ thị hàm số \(y = {x^3} + 3{x^2} - 2\) có các điểm cực đại A(-2;2) và điểm cực tiểu B(0;-2) thì phương trình \({x^3} + 3{x^2} - 2 = m\) có hai nghiệm khi:
- A. \( - 2 < m < 2\)
- B. \(m = - 2\) hoặc m=2
- C. m>2
- D. m<-2
-
Câu 33: Mã câu hỏi: 18158
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB=8a, AC=6a, hình chiếu của A’ trên (ABC) trùng với trung điểm của BC, AA’=10a. Thể tích khối lăng trụ ABC.A’B’C’ là:
- A. \(120\sqrt 3 {a^3}.\)
- B. \(15\sqrt 3 {a^3}.\)
- C. \(405\sqrt 3 {a^3}.\)
- D. \(960\sqrt 3 {a^3}.\)
-
Câu 34: Mã câu hỏi: 18161
Cho hình lăng trụ ABC.A’B’C’, trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA’=3A’M, BB’=3B’N. Mặt phẳng (C’MN) chia khối lăng trụ đã cho thành hai phần. Gọi \({V_1}\) là thể tích của khối chốp C’.A’B’MN, \({V_2}\) là thể tích của khối đa diện ABCMNC’. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
- A. \(\frac{{{V_1}}}{{{V_2}}} = \frac{4}{7}.\)
- B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{2}{7}.\)
- C. \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{7}.\)
- D. \(\frac{{{V_1}}}{{{V_2}}} = \frac{3}{7}.\)
-
Câu 35: Mã câu hỏi: 18162
Cho hình chóp S.ABCD sao cho hai tam giác ADB và DBC có diện tích bằng nhau. Lấy điểm M, N, P, Q trên các cạnh SA, SB, SC, SD sao cho \(SA = 2SM,SB = 3SN,SC = 4SP,SD = 5SQ.\) Gọi \({V_1} = {V_{S.ABCD}},{V_2} = {V_{S.MNPQ}}.\) Chọn phương án đúng:
- A. \({V_1} = 40{V_2}\)
- B. \({V_1} = 20{V_2}\)
- C. \({V_1} = 60{V_2}\)
- D. \({V_1} = 120{V_2}\)
-
Câu 36: Mã câu hỏi: 18173
Tìm giá trị nhỏ nhất của hàm số \(y = \sqrt 2 \cos 2x + 4\sin x\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right].\)
- A. \(\mathop {\min }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = 4 - \sqrt 2 .\)
- B. \(\mathop {\min }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = 2\sqrt 2 .\)
- C. \(\mathop {\min }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = \sqrt 2 .\)
- D. \(\mathop {\min }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = 0.\)
-
Câu 37: Mã câu hỏi: 18174
Đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 2} }}{{x - 1}}\) có bao nhiêu đường tiệm cận?
- A. 1
- B. 0
- C. 2
- D. 3
-
Câu 38: Mã câu hỏi: 18175
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB=2a, góc giữa (SBC) và mặt đáy bằng \({60^0}.\) Thể tích khối chóp S.ABC là:
- A. \(\frac{{125\sqrt 2 {a^3}}}{6}\)
- B. \(\frac{{3\sqrt 6 {a^3}}}{4}\)
- C. \(\frac{{16\sqrt 2 {a^3}}}{3}\)
- D. \(\frac{{2\sqrt 6 {a^3}}}{3}\)
-
Câu 39: Mã câu hỏi: 18176
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
- A. \(y = - {x^4} + 2{x^2} + 1\)
- B. \(y = {x^4} - 3{x^2} + 1\)
- C. \(y = {x^4} - 2{x^2} + 1\)
- D. \(y = - {x^4} - 2{x^2} + 1\)
-
Câu 40: Mã câu hỏi: 18262
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB=a, SA=5a. Gọi D, E là hình chiếu của A trên SB, SC. Tính thể tích khối A.BCDE.
- A. \(\frac{{85{a^3}}}{{1352}}\)
- B. \(\frac{{22{a^3}}}{{289}}\)
- C. \(\frac{{19{a^3}}}{{200}}\)
- D. \(\frac{{3{a^3}}}{{25}}\)
-
Câu 41: Mã câu hỏi: 18263
Hàm số \(y = {x^4} - 2{x^2} - 1\) đồng biến trên khoảng nào sau đây?
- A. \(( - 1;0);(1; + \infty )\)
- B. \(\left( { - \infty ; + \infty } \right)\)
- C. \(( - \infty ; - 1);(0;1)\)
- D. \(( - 1;0);(0;1)\)
-
Câu 42: Mã câu hỏi: 18265
Cho lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi cạnh 3a, góc \(\widehat {BAD} = {120^0};AA' = 3a.\) Tình thể tích khối lăng trụ đã cho.
- A. \(2\sqrt 3 {a^3}.\)
- B. \(\frac{{27\sqrt 3 {a^3}}}{2}.\)
- C. \(40\sqrt 3 {a^3}.\)
- D. \(\sqrt 3 {a^3}.\)
-
Câu 43: Mã câu hỏi: 18267
Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua một con sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100 m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sĩ 1 Km theo đường chim bay và chiến sĩ cách bờ bên kia 100m.
- A. \(\frac{{200\sqrt 2 }}{3}\,(m).\)
- B. \(75\sqrt 2 \,(m).\)
- C. \(75\sqrt 3 \,(m).\)
- D. \(\frac{{200\sqrt 3
-
Câu 44: Mã câu hỏi: 18268
Trong hệ tọa độ Oxy có 8 điểm nằm trên tia Oxvà 5 điểm nằm trên tia Oy. Nối một điểm trên tia Ox và một điểm trên tia Oy ta được 40 đoạn thẳng. Hỏi 40 đoạn thẳng này cắt nhau tại bao nhiêu giao điểm nằm trong góc phần tư thứ nhất của hệ trục tọa độ xOy (Biết rằng không có bất kì 3 đoạn thẳng nào đồng quy tại 1 điểm).
- A. 260
- B. 290
- C. 280
- D. 270
-
Câu 45: Mã câu hỏi: 18269
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SA thỏa mãn \(SM = \frac{1}{4}SA,SN = \frac{1}{3}SB,SB = 3SC.\) Tính thể tích của khối chóp S.MNP theo V.
- A. \(\frac{V}{5}.\)
- B. \(\frac{V}{4}.\)
- C. \(\frac{V}{3}.\)
- D. \(\frac{V}{2}.\)
-
Câu 46: Mã câu hỏi: 18270
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc \({60^0}.\) Tính thể tích của khối lăng trụ ABC.A’B’C’.
- A. \(\frac{{{a^3}\sqrt 3 }}{{10}}\)
- B. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
- C. \(\frac{{{a^3}\sqrt 3 }}{4}\)
- D. \(\frac{{{a^3}\sqrt 3 }}{8}\)
-
Câu 47: Mã câu hỏi: 18272
Số điểm cực trị của hàm số \(y = {x^4} + 100\) là:
- A. 1
- B. 2
- C. 0
- D. 3
-
Câu 48: Mã câu hỏi: 18275
Cho hàm số \(y = \frac{1}{3}{x^3} - m{x^2} - x + m + 1.\) Tìm m để hàm số có 2 cực trị tại A, B thỏa mãn \(x_A^2 + x_B^2 = 2.\)
- A. \(m = \pm 3\)
- B. \(m = 0\)
- C. \(m = \pm 1\)
- D. \(m = 2\)
-
Câu 49: Mã câu hỏi: 18278
Cho hàm số f(x) xác định trên tập D=(-4;4)\{-1;1}, liên tục trên mỗi khoảng xác định và có \(\mathop {\lim }\limits_{x \to {4^ + }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to {1^ - }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to {1^ + }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to {4^ - }} f(x) = + \infty \). Khẳng định nào sau đây là đúng?
- A. Đồ thị hàm số f(x) có đúng hai tiệm cận đứng là các đường thẳng x= -1 và x = 1.
- B. Đồ thị hàm số f(x) có đúng bốn tiệm cận đứng là các đường thẳng x=-4, x=-1, x=1 và x=4.
- C. Đồ thị hàm số f(x) có đúng hai tiệm cận đứng là các đường thẳng x=-4 và x=4.
- D. Đồ thị hàm số f(x) có sáu tiệm cận đứng.
-
Câu 50: Mã câu hỏi: 18280
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}.\) Mệnh đề nào dưới đây là đúng?
- A. Hàm số đồng biến trên tập xác định.
- B. Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\)
- C. Hàm số nghịch biến trên khoảng \(( - 1; + \infty )\)
- D. Hàm số nghịch biến trên khoảng \(( - \infty ; - 1).\)





.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)

