Bài ôn tập chương Phép dời hình và Phép đồng dạng trong mặt phẳng sẽ giúp các em hệ thống lại toàn bộ kiến thức đã học ở chương I. Thông qua các sơ đồ tư duy, các em sẽ có được cách ghi nhớ bài một cách dễ dàng, hiệu quả.
Tóm tắt lý thuyết
.png)
1.1. Nội dung đã được học
a) Tổng quan
b) Các kí hiệu
c) Biểu thức tọa độ
d) Sơ đồ tính chất
1.2. Ghi nhớ phép biến hình qua sơ đồ tư duy
a) Sơ đồ các phép biến hình
.png)
b) Sơ đồ biểu diễn mối liên hệ giữa các phép biến hình
.png)
Bài tập minh họa
Bài tập 1:
Trong mặt phẳng (Oxy) cho \(\overrightarrow u = \left( {1; - 2} \right)\)
a) Viết phương trình ảnh của mỗi đường trong trường hợp sau:
+) Đường thẳng a có phương trình: 3x-5y+1=0 ?
+) Đường thẳng b có phương trình: 2x+y+100=0
b) Viết phương trình đường tròn ảnh của đường tròn (C ): \({x^2} + {y^2} - 4{\rm{x}} + y - 1 = 0\)
c) Viết phương trình đường (E) ảnh của (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\)
d) Viết phương trình ảnh của (H): \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Hướng dẫn giải:
a) Gọi M(x;y) thuộc các đường đã cho và M’(x’;y’) thuộc các đường ảnh của chúng.
Theo công thức tọa độ của phép tịnh tiến ta có: \(\left\{ \begin{array}{l}x' = 1 + x\\y' = - 2 + y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = x' - 1\\y = y' + 2\end{array} \right.\)
Thay x, y vào phương trình các đường ta có:
Đường thẳng a’: 3(x’-1)-5(y’+2)+1=0 \( \Leftrightarrow \)3x’-5y’-12=0
Đường thẳng b’: 2(x’-1)+(y’+2)+100=0 hay : 2x’+y’+100=0
b) Đường tròn (C’): \({\left( {x' - 1} \right)^2} + {\left( {y' + 2} \right)^2} - 4\left( {x' - 1} \right) + y' + 2 - 1 = 0\)
Hay: \({x^2} + {y^2} - 6{\rm{x}} + 5y + 10 = 0\)
c) Đường (E’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{9} + \frac{{{{\left( {y' + 2} \right)}^2}}}{4} = 1 \Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{9} + \frac{{{{\left( {y + 2} \right)}^2}}}{4} = 1\)
d) Đường (H’): \(\frac{{{{\left( {x' - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y' + 2} \right)}^2}}}{9} = 1 \Leftrightarrow \frac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \frac{{{{\left( {y + 2} \right)}^2}}}{9} = 1\).
Bài tập 2:
Cho điểm M(2;-3). Tìm ảnh của điểm M qua phép đối xứng trục d: y-2x=0.
Hướng dẫn giải:
Gọi N(x;y) là điểm đối xứng với M qua d và H là trung điểm của MN thì M,N đối xứng nhau qua d thì điều kiện là: \(\left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow U = 0\quad \left( 1 \right)\\H \in d\quad \quad \left( 2 \right)\end{array} \right.\,\)
Ta có: \(\overrightarrow {MN} = \left( {x - 2;y + 3} \right)\quad \overrightarrow U = \left( {1;2} \right)\quad H = \left( {\frac{{x + 2}}{2};\frac{{y - 3}}{2}} \right)\).
Điều kiện (*) \( \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right).1 + \left( {y + 3} \right).2 = 0\\\frac{{x + 2}}{2} = \frac{{y - 3}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y + 4 = 0\\y = x + 5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}y = \frac{1}{3}\\x = - \frac{{14}}{3}\end{array} \right. \Rightarrow N = \left( { - \frac{{14}}{3};\frac{1}{3}} \right).\)
Bài tập 3:
Trong mặt phẳng Oxy cho đường tròn (O;R) : \({x^2} + {y^2} + 2{\rm{x}} - 6y + 6 = 0\)và (E) : \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) điểm I(1;2). Tìm ảnh của (O;R) và (E) qua phép đối xứng tâm I.
Hướng dẫn giải:
Gọi M(x;y) là điểm bất kỳ thuộc (O;R) và (E).
M’(x’;y’) là ảnh của M qua phép đối xứng tâm I.
Khi đó I là trung điểm của MM’ nên ta có:
\(\left\{ \begin{array}{l}{x_I} = \frac{{x + x'}}{2}\\{y_I} = \frac{{y + y'}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 2.1 - x\\y' = 2.2 - y\end{array} \right.\)
\(\Rightarrow \left\{ \begin{array}{l}x = 2 - x'\\y = 4 - y'\end{array} \right. \Rightarrow \left[ \begin{array}{l}{\left( {2 - x'} \right)^2} + {\left( {4 - y'} \right)^2} + 2\left( {2 - x'} \right) - 6\left( {4 - y'} \right) + 6 = 0\\\frac{{{{\left( {2 - x'} \right)}^2}}}{9} + \frac{{{{\left( {4 - y'} \right)}^2}}}{4} = 1\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0\\\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\end{array} \right.\)
Vậy ảnh của (O;R) và (E) qua phép đối xứng tâm I có phương trình lần lượt là:
\({x^2} + {y^2} - 6{\rm{x}} - 2y + 6 = 0;\,\,\frac{{{{\left( {2 - x} \right)}^2}}}{9} + \frac{{{{\left( {4 - y} \right)}^2}}}{4} = 1\).
Bài tập 4:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O): \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4.\) Tìm phương trình đường tròn (O’) là ảnh của (O) qua phép vị tự tâm O tỉ số k=2.
Hướng dẫn giải:
Tâm I của (O) có tọa độ I(1;1) bán kính R=2.
Nếu (O’) có tâm là J và bán kính R’ là ảnh của (O) qua phép vị tự tâm O ta có đẳng thức vectơ:
\(\overrightarrow {{\rm{OJ}}} = 2\overrightarrow {OI} \Leftrightarrow \left\{ \begin{array}{l}x' - 0 = 2.1\\y' - 0 = 2.1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 2\\y' = 2\end{array} \right. \Rightarrow J\left( {2;2} \right)\).
R’=2R=2.2=4.
Vậy (O’): \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 16\).
3. Luyện tập Bài 9 chương 1 hình học 11
Bài ôn tập chương Phép dời hình và Phép đồng dạng trong mặt phẳng sẽ giúp các em hệ thống lại toàn bộ kiến thức đã học ở chương I. Thông qua các sơ đồ tư duy, các em sẽ có được cách ghi nhớ bài một cách dễ dàng, hiệu quả.
3.1 Trắc nghiệm về phép dời hình và Phép đồng dạng trong mặt phẳng
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Ôn tập chương I để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. Hình lục giác đều.
- B. Hình gồm hai đường thẳng cắt nhau.
- C. Hình gồm hai đường thẳng song song.
- D. Hình gồm hai đường tròn có bán kính bằng nhau.
-
- A. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
- B. Phép đối xứng trục biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
- C. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
- D. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
-
- A. Có phép tịnh tiến biến mọi điểm thành chính nó.
- B. Có phép đối xứng trục biến mọi điểm thành chính nó.
- C. Có phép quay biến mọi điểm thành chính nó.
- D. Có phép vị tự biến mọi điểm thành chính nó.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK và Nâng Cao về phép dời hình và Phép đồng dạng trong mặt phẳng
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Ôn tập chương I sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.
Bài tập 1 trang 33 SGK Hình học 11
Bài tập 2 trang 33 SGK Hình học 11
Bài tập 3 trang 33 SGK Hình học 11
Bài tập 4 trang 34 SGK Hình học 11
Bài tập 1 trang 34 SGK Hình học 11
Bài tập 2 trang 34 SGK Hình học 11
Bài tập 3 trang 34 SGK Hình học 11
Bài tập 4 trang 34 SGK Hình học 11
Bài tập 5 trang 34 SGK Hình học 11
Bài tập 6 trang 34 SGK Hình học 11
Bài tập 5 trang 35 SGK Hình học 11
Bài tập 6 trang 35 SGK Hình học 11
Bài tập 7 trang 35 SGK Hình học 11
Bài tập 1 trang 35 SGK Hình học 11
Bài tập 2 trang 35 SGK Hình học 11
Bài tập 3 trang 35 SGK Hình học 11
Bài tập 4 trang 36 SGK Hình học 11
Bài tập 5 trang 36 SGK Hình học 11
Bài tập 6 trang 36 SGK Hình học 11
Bài tập 7 trang 36 SGK Hình học 11
Bài tập 8 trang 36 SGK Hình học 11
Bài tập 9 trang 36 SGK Hình học 11
Bài tập 10 trang 36 SGK Hình học 11
Bài tập 1.31 trang 37 SBT Hình học 11
Bài tập 1.32 trang 37 SBT Hình học 11
Bài tập 1.33 trang 37 SBT Hình học 11
Bài tập 1.34 trang 37 SBT Hình học 11
Bài tập 1.35 trang 37 SBT Hình học 10
Bài tập 1.36 trang 37 SBT Hình học 11
Bài tập 1.37 trang 37 SBT Hình học 11
Bài tập 1.38 trang 38 SBT Hình học 11
Bài tập 1.39 trang 38 SBT Hình học 11
Bài tập 1.40 trang 38 SBT Hình học 11
Bài tập 1.41 trang 38 SBT Hình học 11
Bài tập 1.42 trang 38 SBT Hình học 11
Bài tập 1.43 trang 38 SBT Hình học 11
Bài tập 1.44 trang 38 SBT Hình học 11
Bài tập 1.45 trang 38 SBT Hình học 11
Bài tập 1.46 trang 38 SBT Hình học 11
Bài tập 1.47 trang 38 SBT Hình học 11
Bài tập 1.48 trang 38 SBT Hình học 11
Bài tập 1.49 trang 39 SBT Hình học 11
Bài tập 1.50 trang 39 SBT Hình học 11
Bài tập 1.51 trang 39 SBT Hình học 11
Bài tập 1.52 trang 39 SBT Hình học 11
Bài tập 1.53 trang 39 SBT Hình học 11
Bài tập 1.54 trang 39 SBT Hình học 11
Bài tập 1.55 trang 39 SBT Hình học 11
Bài tập 1.56 trang 39 SBT Hình học 11
Bài tập 1.57 trang 39 SBT Hình học 11
Bài tập 1.58 trang 39 SBT Hình học 11
Bài tập 1.59 trang 40 SBT Hình học 11
Bài tập 1.60 trang 40 SBT Hình học 11
Bài tập 1.61 trang 40 SBT Hình học 11
Bài tập 1.62 trang 40 SBT Hình học 11
Bài tập 1.63 trang 40 SBT Hình học 11
Bài tập 1.64 trang 40 SBT Hình học 11
Bài tập 1.65 trang 40 SBT Hình học 11
Bài tập 1.66 trang 40 SBT Hình học 11
Bài tập 1.67 trang 41 SBT Hình học 11
Bài tập 1.68 trang 41 SBT Hình học 11
Bài tập 1.69 trang 41 SBT Hình học 11
Bài tập 1.70 trang 41 SBT Hình học 11
Bài tập 1.71 trang 41 SBT Hình học 11
Bài tập 1.72 trang 41 SBT Hình học 11
Bài tập 1.73 trang 41 SBT Hình học 11
Bài tập 1.74 trang 41 SBT Hình học 11
Bài tập 1.75 trang 42 SBT Hình học 11
Bài tập 1.76 trang 42 SBT Hình học 11
Bài tập 1.77 trang 42 SBT Hình học 11
Bài tập 1.78 trang 42 SBT Hình học 11
Bài tập 1 trang 34 SGK Hình học 11 NC
Bài tập 2 trang 34 SGK Hình học 11 NC
Bài tập 3 trang 34 SGK Hình học 11 NC
Bài tập 4 trang 34 SGK Hình học 11 NC
Bài tập 5 trang 34 SGK Hình học 11 NC
Bài tập 6 trang 34 SGK Hình học 11 NC
Bài tập 7 trang 34 SGK Hình học 11 NC
Bài tập 8 trang 35 SGK Hình học 11 NC
Bài tập 9 trang 35 SGK Hình học 11 NC
Bài tập 1 trang 35 SGK Hình học 11 NC
Bài tập 2 trang 35 SGK Hình học 11 NC
Bài tập 3 trang 35 SGK Hình học 11 NC
Bài tập 4 trang 35 SGK Hình học 11 NC
Bài tập 5 trang 35 SGK Hình học 11 NC
Bài tập 6 trang 35 SGK Hình học 11 NC
Bài tập 7 trang 36 SGK Hình học 11 NC
Bài tập 8 trang 36 SGK Hình học 11 NC
Bài tập 9 trang 36 SGK Hình học 11 NC
Bài tập 10 trang 36 SGK Hình học 11 NC
Bài tập 11 trang 36 SGK Hình học 11 NC
Bài tập 12 trang 36 SGK Hình học 11 NC
4. Hỏi đáp về bài 9 chương 1 hình học 11
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 11 HỌC247





.PNG)
.PNG)
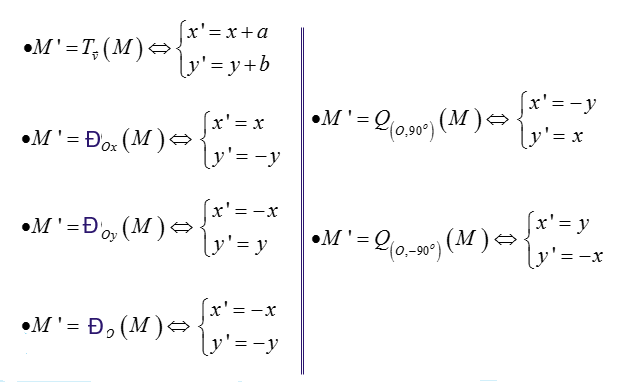
.PNG)







