Bài tập 3 trang 34 SGK Hình học 11 NC
Cho đường thẳng d đi qua hai điểm phân biệt P, Q và hai điểm A, B nằm về một phía đối với d. Hãy xác định trên d hai điểm M, N sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \) và AM + BN bé nhất
Hướng dẫn giải chi tiết
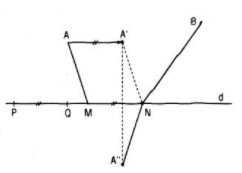
Giả sử hai điểm M, N nằm trên d sao cho \(\overrightarrow {MN} = \overrightarrow {PQ} \)
Lấy điểm A’ sao cho \(\overrightarrow {AA'} = \overrightarrow {PQ} \) thì điểm A’ hoàn toàn xác định và AMNA’ là hình bình hành nên AM = A’N
Ta có: AM + BN = A’N + BN
Gọi A” là điểm đối xứng của A’ qua d, khi đó:
A’N + BN = A”N + BN ≥ A”B
Từ đó ta suy ra AM + BN nhỏ nhất khi N là giao điểm của BA” với d
Từ đó tìm được điểm M thỏa \(\overrightarrow {MN} = \overrightarrow {AA'} = \overrightarrow {PQ} \)
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 1 trang 34 SGK Hình học 11 NC
Bài tập 2 trang 34 SGK Hình học 11 NC
Bài tập 4 trang 34 SGK Hình học 11 NC
Bài tập 5 trang 34 SGK Hình học 11 NC
Bài tập 6 trang 34 SGK Hình học 11 NC
Bài tập 7 trang 34 SGK Hình học 11 NC
Bài tập 8 trang 35 SGK Hình học 11 NC
Bài tập 9 trang 35 SGK Hình học 11 NC
Bài tập 1 trang 35 SGK Hình học 11 NC
Bài tập 2 trang 35 SGK Hình học 11 NC
Bài tập 3 trang 35 SGK Hình học 11 NC
Bài tập 4 trang 35 SGK Hình học 11 NC
Bài tập 5 trang 35 SGK Hình học 11 NC
Bài tập 6 trang 35 SGK Hình học 11 NC
Bài tập 7 trang 36 SGK Hình học 11 NC
Bài tập 8 trang 36 SGK Hình học 11 NC
Bài tập 9 trang 36 SGK Hình học 11 NC
Bài tập 10 trang 36 SGK Hình học 11 NC





