Bài tập 5 trang 34 SGK Hình học 11 NC

92 BT SGK

Cho tam giác ABC nội tiếp trong đường tròn (O) và một điểm M thay đổi trên (O). Gọi M₁ là điểm đối xứng với M qua A, M₂ là điểm đối xứng với M₁ qua B, M₃ là điểm đối xứng với M₂qua C

a. Chứng tỏ rằng phép biến hình F biến điểm M thành M₃ là một phép đối xứng tâm

b. Tìm quỹ tích điểm M₃

Hướng dẫn giải chi tiết

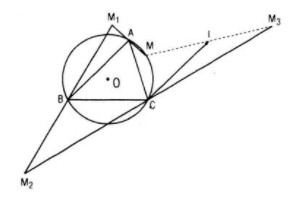
a) Gọi I là trung điểm của MM₃, ta chứng minh I là điểm cố định

Thật vậy, ta có:

\(\begin{array}{l}
\overrightarrow {CI} = \frac{1}{2}(\overrightarrow {CM} + \overrightarrow {C{M_3}} )\\
= \frac{1}{2}(\overrightarrow {CM} + \overrightarrow {{M_2}C} )\\
= \frac{1}{2}\overrightarrow {{M_2}M} = \overrightarrow {BA}
\end{array}\)

Vậy điểm I cố định, do đó phép biến hình F biến M thành M₃ là phép đối xứng qua điểm I

b) Quỹ tích điểm M₃ là đường tròn (O’), ảnh của đường tròn (O) qua phép đối xứng tâm với tâm I.

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 5 trang 34 SGK Hình học 11 NC HAY thì click chia sẻ

YOMEDIA