Bài tập 1 trang 178 SGK Đại số & Giải tích 11

Lý thuyết

63 BT SGK

643 FAQ

Giải bài 1 tr 178 sách GK Toán ĐS & GT lớp 11

Cho hàm số y = cos2x.

a) Chứng minh rằng \(cos2(x+k\pi )=cos2x\) với mọi số nguyên k. Từ đó về đồ thị (C) của hàm số y = cos2x.

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ \(x=\frac{\pi }{3}.\)

c) Tìm tập xác định của hàm số \(z=\sqrt{\frac{1-cos2x}{1+cos^22x}}\)

ATNETWORK

Hướng dẫn giải chi tiết

Câu a:

Ta có: \(cos2(x+k\pi )=cos(2x+2k\pi )=cos2x, \forall k\in \mathbb{Z}, \forall x\in \mathbb{R}\)

Sử dụng tính chất trên, ta chỉ cần vẽ đồ thị hàm số \(y=cos2x\) trên miền \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\), từ đó suy ra đồ thị hàm số \(y=cos2x\) trên \(\mathbb{R}\).

Đồ thị hàm số \(y=cos2x\) trên miền \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\).

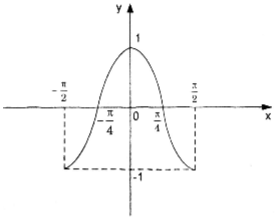
Đồ thị hàm số \(y=cos2x\) trên \(\mathbb{R}\).

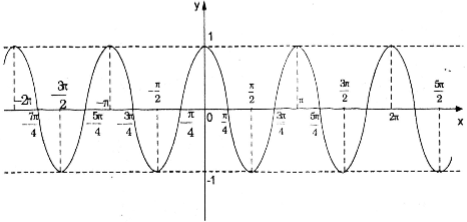
Câu b:

Ta có: \(y'=-2sin2x\Rightarrow y'\left ( \frac{\pi }{3} \right )=-2sin\frac{2\pi }{3}=-\sqrt{3}\)

Mặt khác điểm trên đồ thị (C) có hoành độ là \(\frac{\pi }{3}\) thì có tung độ \(y=cos\frac{2\pi }{3}\) hay \(y=-\frac{1}{2}\). Vì vậy phương trình tiếp tuyến tại điểm \(\left ( \frac{\pi }{3};-\frac{1}{2} \right )\) có dạng: \(y=-\sqrt{3}\left ( x-\frac{\pi }{3} \right )-\frac{1}{2}\Leftrightarrow y=- \sqrt{3}x+\frac{\sqrt{3}\pi }{3}-\frac{1}{2}\)

Câu c:

Dễ thấy \(1+cos^22x\geq 1, \forall x\in \mathbb{R}\), do đó hàm số đã cho được xác định khi và chỉ khi \(1-cos2x\geq 0\Leftrightarrow cos2x\leq 1\) được thoả mãn với mọi \(x\in \mathbb{R}\)

Vậy tập xác định của hàm số \(z=\sqrt{\frac{1-cos2x}{1+cos^22x}}\) là tập \(\mathbb{R}\).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1 trang 178 SGK Đại số & Giải tích 11 HAY thì click chia sẻ

YOMEDIA

Cho hàm số \(f\left( x \right) = \frac{1}{{{x^2} + 1}}\). Tập nghiệm của bất phương trình \(f'\left( x \right) > 0\) là câu?

bởi minh dương 18/07/2021

A. \(\mathbb{R}\) B. \(\emptyset \)

C. \(\left( { - \infty ;0} \right)\) D. \(\left( {0; + \infty } \right)\)

Theo dõi (0) 1 Trả lời
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {x + 3} - 2}}{{{x^2} - 1}},x > 1\\ax + 2,\,\,\,\,\,\,\,\,\,\,\,x \le 1\end{array} \right.\). Giá trị của \(a\) để hàm số liên tục tại \(x = 1\) là bao nhiêu?

bởi thanh hằng 18/07/2021

A. \(a = - \frac{{17}}{8}\) B. \(a = \frac{{15}}{8}\)

C. \(a = - \frac{{15}}{8}\) D. \(a = \frac{{17}}{8}\)

Theo dõi (0) 1 Trả lời
Có giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{\cos 2018x - \cos 2019x}}{x}\) bằng

bởi Tra xanh 18/07/2021

A. \(0\) B. \( + \infty \)

C. \( - \infty \) D. \(\frac{{4037}}{2}\)

Theo dõi (0) 1 Trả lời
Đạo hàm của hàm số \(y = \sqrt {\sin x + 2} \) là bằng

bởi Phung Meo 18/07/2021

A. \(y' = \frac{{\cos x}}{{\sqrt {\sin x + 2} }}\)

B. \(y' = - \frac{{\cos x}}{{2\sqrt {\sin x + 2} }}\)

C. \(y' = \frac{1}{{2\sqrt {\sin x + 2} }}\)

D. \(y' = \frac{{\cos x}}{{2\sqrt {\sin x + 2} }}\)

Theo dõi (0) 1 Trả lời
Biết giới hạn \(\mathop {\lim }\limits_{x \to 2018} \frac{{{x^2} - 2019x + 2018}}{{x - 2018}}\) bằng

bởi Suong dem 18/07/2021

A. \(2020\) B. \(2017\)

C. \(2019\) D. \(2018\)

Theo dõi (0) 1 Trả lời
Nếu có \(f\left( x \right) = x\sin x\) thì \(f'\left( {\frac{{7\pi }}{2}} \right)\) bằng

bởi Phạm Khánh Linh 18/07/2021

A. \( - 1\) B. \(\frac{{7\pi }}{2}\)

C. \(1\) D. \(7\pi \)

Theo dõi (0) 1 Trả lời
Biết hàm số \(y = {x^4} - 2{x^2} - 1\) có đồ thị \(\left( C \right)\). Số tiếp tuyến song song với trục hoành của đồ thị \(\left( C \right)\) là

bởi Nguyễn Hạ Lan 18/07/2021

A. \(1\) B. \(2\)

C. \(3\) D. \(0\)

Theo dõi (0) 1 Trả lời
Trong bốn giới hạn cho sau đây, giới hạn nào bằng \(2?\)

bởi Truc Ly 18/07/2021

A. \(\lim \frac{{n + 1}}{{2n - 1}}\)

B. \(\lim \frac{{1 - 4n}}{{2n + 3}}\)

C. \(\lim \frac{{2n + 3}}{{n - 5}}\)

D. \(\lim \frac{{{n^2} + 2n + 3}}{{{n^2} - 2n + 2}}\)

Theo dõi (0) 1 Trả lời
Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} - 3x + 1} \right)\) là bằng

bởi Tran Chau 17/07/2021

A. \( + \infty \) B. \( - \infty \)

C. \( - 1\) D. \(1\)

Theo dõi (0) 1 Trả lời
Cho hàm số \(f\left( x \right) = \frac{{{x^2} + 2}}{{x - 2}}\) . Giá trị \(f'\left( 1 \right)\) là bằng bao nhiêu

bởi bich thu 18/07/2021

A. \(5\) B. \( - 3\)

C. \(4\) D. \( - 5\)

Theo dõi (0) 1 Trả lời
Cho biết giới hạn \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x - \sqrt {x + 3} }}{{x + 1}}\) bằng:

bởi Dương Minh Tuấn 18/07/2021

A. \( + \infty \) B. \(1\)

C. \( - \infty \) D. \(0\)

Theo dõi (0) 1 Trả lời