Bài tập 2 trang 223 SGK Toán 11 NC
Giải phương trình
\(\tan x = \cot 2x\)
Biểu diễn các nghiệm trên đường tròn lượng giác.
Hướng dẫn giải chi tiết
Điều kiện
\(\begin{array}{l}
\cos x.\sin 2x \ne 0\\
\Leftrightarrow \left\{ \begin{array}{l}
\sin x \ne 0\\
\cos x \ne 0
\end{array} \right. \Leftrightarrow x \ne k\pi 2
\end{array}\)
\(\begin{array}{l}
\tan x = \cot 2x \Leftrightarrow \frac{{\sin x}}{{\cos x}} = \frac{{\cos 2x}}{{\sin 2x}}\\
\Leftrightarrow \cos x\cos 2x - \sin x\sin 2x = 0\\
\Leftrightarrow \cos 3x = 0 \Leftrightarrow \cos x\left( {4{{\cos }^2}x - 3} \right)\\
\Leftrightarrow {\cos ^2}x = \frac{3}{4} \Leftrightarrow \frac{{1 + \cos 2x}}{2} = \frac{3}{4}\\
\Leftrightarrow \cos 2x = \frac{1}{2}\\
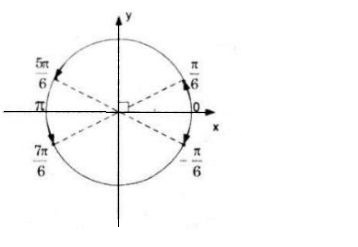
\Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \left( {k \in Z} \right)
\end{array}\)
Biểu diễn nghiệm trên đường tròn được 4 điểm.
-- Mod Toán 11 HỌC247
-


Hãy giải pt: \(10\cos x - 5 = 0\,;\,\,\,\)
bởi thùy trang
 17/07/2021
17/07/2021
Hãy giải pt: \(10\cos x - 5 = 0\,;\,\,\,\)
Theo dõi (0) 1 Trả lời -


Trong tuần lễ cấp cao Apec diễn ra từ ngày 06 đến ngày 11 tháng 11 năm 2017 tại Đà Nẵng, có 21 nên kinh tế thành viên tham dự, trong đó có 12 nền kinh tế sáng lập Apec. Tại một cuộc họp báo, mỗi nền kinh tế thành viên cử một đại diện tham gia. Một phóng viên đã chọn ngẫu nhiên 5 đại diện để phỏng vấn. Hãy tính xác suất để 5 đại diện đó có cả đại diện của nền kinh tế thành viên sáng lập Apec và nền kinh tế thành viên không sáng lập Apec.
bởi Thanh Thanh
 17/07/2021
17/07/2021
Trong tuần lễ cấp cao Apec diễn ra từ ngày 06 đến ngày 11 tháng 11 năm 2017 tại Đà Nẵng, có 21 nên kinh tế thành viên tham dự, trong đó có 12 nền kinh tế sáng lập Apec. Tại một cuộc họp báo, mỗi nền kinh tế thành viên cử một đại diện tham gia. Một phóng viên đã chọn ngẫu nhiên 5 đại diện để phỏng vấn. Hãy tính xác suất để 5 đại diện đó có cả đại diện của nền kinh tế thành viên sáng lập Apec và nền kinh tế thành viên không sáng lập Apec.
Theo dõi (0) 1 Trả lời -


Giải phương trình sau đây: \(\left[ {1 + \cos \left( {x + \dfrac{\pi }{2}} \right)} \right]{\tan ^2}x - \cos x = 1\).
bởi Thùy Trang
 17/07/2021
17/07/2021
Giải phương trình sau đây: \(\left[ {1 + \cos \left( {x + \dfrac{\pi }{2}} \right)} \right]{\tan ^2}x - \cos x = 1\).
Theo dõi (0) 1 Trả lời -


Giải phương trình sau đây: \(\cos 2x - 5\sin x - 3 = 0\).
Theo dõi (0) 1 Trả lời -


Lấy ngẫu nhiên đồng thời 4 viên bi từ trong hộp đựng 16 viên bi trong đó có 5 viên bi màu xanh, 4 viên bi màu đỏ và 7 viên bi màu vàng. Hãy tính xác suất để trong 4 viên bi lấy ra có đúng 2 viên bi màu vàng.
bởi Trong Duy
 17/07/2021
17/07/2021
Lấy ngẫu nhiên đồng thời 4 viên bi từ trong hộp đựng 16 viên bi trong đó có 5 viên bi màu xanh, 4 viên bi màu đỏ và 7 viên bi màu vàng. Hãy tính xác suất để trong 4 viên bi lấy ra có đúng 2 viên bi màu vàng.
Theo dõi (0) 1 Trả lời -


Giải pt: \(2{\sin ^2}x + 3\sqrt 2 \sin \,x + 2 = 0\).
bởi May May
 17/07/2021
17/07/2021
Giải pt: \(2{\sin ^2}x + 3\sqrt 2 \sin \,x + 2 = 0\).
Theo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị của tham số của m để phương trình \(\sin 2x + m\cos x - 4\sin \,x - 2m = 0\) có nghiệm.
bởi Nhật Mai
 17/07/2021
17/07/2021
Tìm tất cả các giá trị của tham số của m để phương trình \(\sin 2x + m\cos x - 4\sin \,x - 2m = 0\) có nghiệm.
Theo dõi (0) 1 Trả lời -


Hãy giải phương trình sau đây: \(3A_{x - 2}^2 - 2C_x^{x - 2} - 2{x^2} + 38 = 0\)
bởi Thụy Mây
 16/07/2021
16/07/2021
Hãy giải phương trình sau đây: \(3A_{x - 2}^2 - 2C_x^{x - 2} - 2{x^2} + 38 = 0\)
Theo dõi (0) 1 Trả lời -


Có một lớp học gồm 16 học sinh nam và 14 học sinh nữ. Giáo viên chủ nhiệm chọn ngẫu nhiên 6 học sinh để tham gia lớp học về “AN TOÀN GIAO THÔNG”. Hãy tính xác suất để trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam?
bởi Nguyễn Vân
 17/07/2021
17/07/2021
Có một lớp học gồm 16 học sinh nam và 14 học sinh nữ. Giáo viên chủ nhiệm chọn ngẫu nhiên 6 học sinh để tham gia lớp học về “AN TOÀN GIAO THÔNG”. Hãy tính xác suất để trong 6 học sinh được chọn số học sinh nữ gấp đôi số học sinh nam?
Theo dõi (0) 1 Trả lời -


Giải phương trình đã cho sau: \(\sin \,x - \sqrt 3 \cos x = 1\).
Theo dõi (0) 1 Trả lời -


Giải phương trình đã cho sau: \({\sin ^2}x - \cos x + 1 = 0\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 20 trang 181 SGK Đại số & Giải tích 11
Bài tập 1 trang 223 SGK Toán 11 NC
Bài tập 3 trang 223 SGK Toán 11 NC
Bài tập 4 trang 223 SGK Toán 11 NC
Bài tập 5 trang 224 SGK Toán 11 NC
Bài tập 6 trang 224 SGK Toán 11 NC
Bài tập 7 trang 224 SGK Toán 11 NC
Bài tập 8 trang 224 SGK Toán 11 NC
Bài tập 9 trang 224 SGK Toán 11 NC
Bài tập 10 trang 224 SGK Toán 11 NC
Bài tập 11 trang 225 SGK Toán 11 NC
Bài tập 12 trang 225 SGK Toán 11 NC
Bài tập 13 trang 225 SGK Toán 11 NC
Bài tập 14 trang 225 SGK Toán 11 NC
Bài tập 15 trang 225 SGK Toán 11 NC
Bài tập 16 trang 226 SGK Toán 11 NC
Bài tập 17 trang 226 SGK Toán 11 NC
Bài tập 18 trang 226 SGK Toán 11 NC
Bài tập 19 trang 226 SGK Toán 11 NC
Bài tập 20 trang 226 SGK Toán 11 NC
Bài tập 21 trang 226 SGK Toán 11 NC
Bài tập 22 trang 227 SGK Toán 11 NC
Bài tập 23 trang 227 SGK Toán 11 NC





