Bài tập 5 trang 24 SGK Giải tích 12

Lý thuyết10 Trắc nghiệm

31 BT SGK

487 FAQ

Giải bài 5 tr 24 sách GK Toán GT lớp 12

Tính giá trị nhỏ nhất của các hàm số sau:

a) \(y = \left | x \right |\);

b) \(y = x+\frac{4}{x} ( x > 0)\)

ANYMIND360

Toán 12 Chương 1 Bài 3 Trắc nghiệm Toán 12 Chương 1 Bài 3 Giải bài tập Toán 12 Chương 1 Bài 3

Hướng dẫn giải chi tiết bài 5

Với bài 5 ta áp dụng cách giải sau:

Để tìm GTLN, GTNN của hàm số \(y=f(x)\) xác định trên tập hợp D, ta tiến hành khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số đưa ra kết luận về GTLN và GTNN của hàm số.

Có nhiều trường hợp ta có thể nhìn vào hàm số và đánh giá ngay được giá trị lớn nhất và nhỏ nhất của hàm số, cụ thể ở đây là câu a bài 5.

Áp dụng ta giải câu a, b bài 5 như sau:

Câu a:

Cách 1: Ứng dụng đạo hàm

\(y = |x| = \left\{ \begin{gathered} x\text{ nếu }x \geqslant 0 \hfill \\ - x\text{ nếu }x < 0 \hfill \\ \end{gathered} \right.\)

Tập xác định \(D=\mathbb{R}.\)

\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = 1.\)

\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f(x) - f(0)}}{{x - 0}} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{x} = - 1.\)

Vậy hàm số không có đạo hàm tại x=0.

Bảng biến thiên:

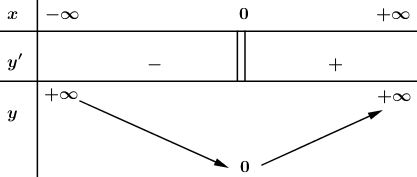
Từ bảng biến thiên ta thấy \(\min y = y(0) = 0.\)

Cách 2: Dùng tính chất của hàm số

Tập xác định \(D=\mathbb{R}.\)

Ta có: \(\left| x \right| \ge 0,\forall x \in\mathbb{R} ,\) dấu bằng xảy ra khi x=0. Vậy \(\min y = y(0) = 0.\)

Câu b:

Tập xác định \(D = \left( {0; + \infty } \right).\)

\(y' = 0 \Leftrightarrow x = 2.\)

\(y=x+\dfrac{4}{x}\ \ \ \left( x>0 \right).\)

Ta có: \(y'=1-\dfrac{4}{{{x}^{2}}}\)

\(\Rightarrow y'=0\Leftrightarrow 1-\dfrac{4}{{{x}^{2}}}=0\)

\(\Leftrightarrow {{x}^{2}}-4=0\Leftrightarrow \left[ \begin{align}& x=-2\notin \left( 0;+\infty \right) \\ & x=2\in \left( 0;+\infty \right) \\ \end{align} \right.\)

Bảng biến thiên:

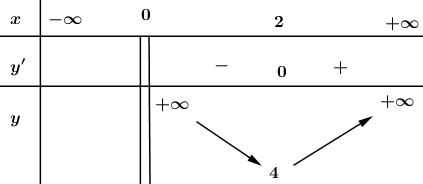
Vậy giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{x\left( {0; + \infty } \right)} = y(2) = 4.\)

Với câu b bài 5 ta cũng có thể dùng bất đẳng thức côsi để giải.

-- Mod Toán 12 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 5 trang 24 SGK Giải tích 12 HAY thì click chia sẻ

Tìm giá trị của \(m\) để hàm số \(f\left( x \right) = {{{x^2} + mx - 1} \over {x - 1}}\) có cực đại và cực tiểu.

bởi Bao Nhi 01/06/2021

Tìm giá trị của \(m\) để hàm số \(f\left( x \right) = {{{x^2} + mx - 1} \over {x - 1}}\) có cực đại và cực tiểu.

Theo dõi (0) 1 Trả lời
Tìm cực trị của hàm số sau: \(f\left( x \right) = x + \sqrt {{x^2} - 1} \).

bởi Nguyễn Thị Trang 02/06/2021

Tìm cực trị của hàm số sau: \(f\left( x \right) = x + \sqrt {{x^2} - 1} \).

Theo dõi (0) 1 Trả lời
Tìm cực trị của hàm số sau: \(f\left( x \right) = \sqrt {5 - {x^2}} \)

bởi Nguyễn Lê Thảo Trang 02/06/2021

Tìm cực trị của hàm số sau: \(f\left( x \right) = \sqrt {5 - {x^2}} \)

Theo dõi (0) 1 Trả lời
Tìm cực trị của hàm số sau: \(f\left( x \right) = {{{x^3}} \over {x + 1}}\)

bởi thu hảo 01/06/2021

Tìm cực trị của hàm số sau: \(f\left( x \right) = {{{x^3}} \over {x + 1}}\)

Theo dõi (0) 1 Trả lời
Tìm cực trị của hàm số sau: \(f\left( x \right) = {x \over {{x^2} + 1}}\).

bởi Mai Anh 02/06/2021

Tìm cực trị của hàm số sau: \(f\left( x \right) = {x \over {{x^2} + 1}}\).

Theo dõi (0) 1 Trả lời
Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.

bởi Phạm Khánh Linh 01/06/2021

Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng: \(P(n)=480 – 20n\). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.

Theo dõi (0) 1 Trả lời
Xác định vị trí của điểm \(M\) sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.

bởi Phạm Khánh Linh 02/06/2021

Cho một tam giác đều \(ABC\) cạnh \(a\). Người ta dựng một hình chữ nhật \(MNPQ\) có cạnh \(MN\) nằm trên cạnh \(BC\), hai đỉnh \(P\) và \(Q\) theo thứ tự nằm trên hai cạnh \(AC\) và \(AB\) của tam giác. Xác định vị trí của điểm \(M\) sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(y = {\cos ^2}2x - \sin x\cos x + 4\).

bởi Bao Nhi 01/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(y = {\cos ^2}2x - \sin x\cos x + 4\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(y = 2{\sin ^2}x + 2\sin x - 1\).

bởi can tu 01/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(y = 2{\sin ^2}x + 2\sin x - 1\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = x - {1 \over x}\) trên đoạn \(\left( {0;2} \right]\).

bởi Tường Vi 02/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = x - {1 \over x}\) trên đoạn \(\left( {0;2} \right]\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\).

bởi Vũ Hải Yến 02/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = - {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\).

bởi bala bala 01/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = - {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\).

bởi Vũ Hải Yến 02/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\).

bởi Trần Thị Trang 02/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {x^2} + 2x - 5\) trên đoạn \(\left[ { - 2;3} \right]\).

bởi Nguyễn Quang Thanh Tú 01/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: \(f\left( x \right) = {x^2} + 2x - 5\) trên đoạn \(\left[ { - 2;3} \right]\).

Theo dõi (0) 1 Trả lời
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f\left( x \right) = {\sin ^4}x + {\cos ^4}x\).

bởi Tường Vi 01/06/2021

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f\left( x \right) = {\sin ^4}x + {\cos ^4}x\).

Theo dõi (0) 1 Trả lời