Giải bài 1.34 tr 21 SBT Toán 12
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(f\left( x \right) = \sqrt {25 - {x^2}} \) trên đoạn ;
b) \(f\left( x \right) = |{x^2} - 3x + 2|\) trên đoạn ;
c) \(f\left( x \right) = \frac{1}{{\sin x}}\) trên đoạn \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\);
d) \(f\left( x \right) = 2\sin x + \sin 2x\) trên đoạn \(\left[ {0;\frac{{3\pi }}{2}} \right]\).
Hướng dẫn giải chi tiết
\(f'\left( x \right) = \frac{{ - x}}{{\sqrt {25 - {x^2}} }}\)
trên khoảng và trên khoảng
Vậy \(\mathop {\max }\limits_{\left[ { - 4;4} \right]} f\left( x \right) = 5;\)
b) \(f\left( x \right) = |{x^2} - 3x + 2|\) trên đoạn
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(g\left( x \right) = {x^2} - 3x + 2\)
Ta có: \(g'\left( x \right) = 2x - 3;g'\left( x \right) = 0 \Leftrightarrow x = \frac{3}{2}\)
.png)
g\left( x \right)\,\,\,\,khi\,\,{x^2} - 3x + 2 \ge 0\\
- g\left( x \right)\,khi\,\,{x^2} - 3x + 2 < 0
\end{array} \right.\)
nên ta có đồ thị của như sau:
.png)
\(\mathop {\max }\limits_{\left[ { - 10;10} \right]} f\left( x \right) = f\left( { - 10} \right) = 132;\)
c) \(f\left( x \right) = \frac{1}{{\sin x}}\) trên đoạn \(\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]\)
\(f'\left( x \right) = - \frac{{\cos x}}{{{{\sin }^2}x}};\)
trên \(\left[ {\frac{\pi }{3};\frac{\pi }{2}} \right)\) và trên \(\left( {\frac{\pi }{2};\frac{{5\pi }}{6}} \right]\) nên hàm số đạt cực tiểu tại \(x = \frac{\pi }{2}\) và \({f_{CT}} = f\left( {\frac{\pi }{2}} \right) = 1\)
Vậy \(\mathop {\max }\limits_{\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]} f\left( x \right) = 2;\mathop {\min }\limits_{\left[ {\frac{\pi }{3};\frac{{5\pi }}{6}} \right]} f\left( x \right) = 1\)
\(f\prime \left( x \right) = 2\cos x + 2\cos 2x\)
\(\begin{array}{l}
f\prime \left( x \right) = 2\cos x + 2\cos 2x\prime \left( x \right) = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\cos \frac{x}{2} = 0}\\
{\cos \frac{{3x}}{2} = 0}
\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pi }\\
{x = \frac{\pi }{3}}
\end{array}} \right.
\end{array}\)
Ta có:
Từ đó ta có:
-- Mod Toán 12 HỌC247
-


Tìm các tiệm cận của đồ thị hàm số sau: \(y=\dfrac{-x+7}{x+1}\).
Theo dõi (0) 1 Trả lời -


Tìm các tiệm cận của đồ thị hàm số sau: \(y=\dfrac{x}{2-x}\).
Theo dõi (0) 1 Trả lời -


Hãy tính \(\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{1}{x} + 2} \right)\) và nêu nhận xét về khoảng cách \(MH\) khi \(x → 0\) (H.17)
bởi Truc Ly
 31/05/2021
31/05/2021
Tính \(\mathop {\lim }\limits_{x \to 0} \left( {\dfrac{1}{x} + 2} \right)\) và nêu nhận xét về khoảng cách \(MH\) khi \(x → 0\) (H.17)
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hàm số: \(y = {{2 - x} \over {x - 1}}\) (H.16) có đồ thị (C). Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
bởi Nhat nheo
 01/06/2021
01/06/2021
Cho hàm số: \(y = {{2 - x} \over {x - 1}}\) (H.16) có đồ thị (C).
.png)
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
Theo dõi (0) 1 Trả lời -


Cho hàm số f(x), đồ thị của hàm số y=f’(x)là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x)=f(2x) -4xtrên đoạn bằng[-3/2;2] bằng
bởi Hoàng Hùng
 12/05/2021
Cho hàm số f(x), đồ thị của hàm số y=f’(x)là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x)=f(2x) -4xtrên đoạn bằng[-3/2;2] bằngTheo dõi (0) 0 Trả lời
12/05/2021
Cho hàm số f(x), đồ thị của hàm số y=f’(x)là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x)=f(2x) -4xtrên đoạn bằng[-3/2;2] bằngTheo dõi (0) 0 Trả lời -


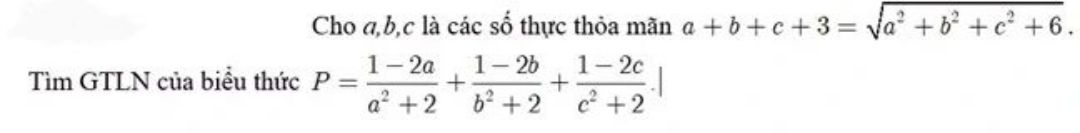 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -

 gtln
gtln Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -

 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Trong tất cả các hình chữ nhật cùng có diện tích \(48 m^2\) , hãy xác định hình chữ nhật có chu vi nhỏ nhất.
bởi Lê Nguyễn Hạ Anh
 01/03/2021
Theo dõi (0) 2 Trả lời
01/03/2021
Theo dõi (0) 2 Trả lời -


Trong số các hình chữ nhật cùng có chu vi \(16 cm\), hãy tìm hình chữ nhật có diện tích lớn nhất.
bởi Cam Ngan
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Lập bảng biến thiên của hàm số \(\displaystyle f(x) = -{{ 1} \over {1 + {x^2}}}\). Từ đó suy ra giá trị nhỏ nhất của f(x) trên tập xác định.
bởi A La
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = \sqrt {5 - 4{\rm{x}}}\) trên đoạn \([-1;1]\).
bởi Mai Trang
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = {{2 - x} \over {1 - x}}\) trên các đoạn \([2;4]\) và \([-3;-2]\).
bởi Minh Thắng
 28/02/2021
Theo dõi (0) 1 Trả lời
28/02/2021
Theo dõi (0) 1 Trả lời -


Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y{\rm{ }} = {\rm{ }}{x^4}-{\rm{ }}3{x^2} + {\rm{ }}2\) trên các đoạn \([0;3]\) và \([2;5]\).
bởi minh dương
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Tính GTLN,GTNN của hàm số f(x)= 2(cos^2)x 2cos x 1
bởi Đỗ Thúy Quỳnh
 15/02/2021
15/02/2021
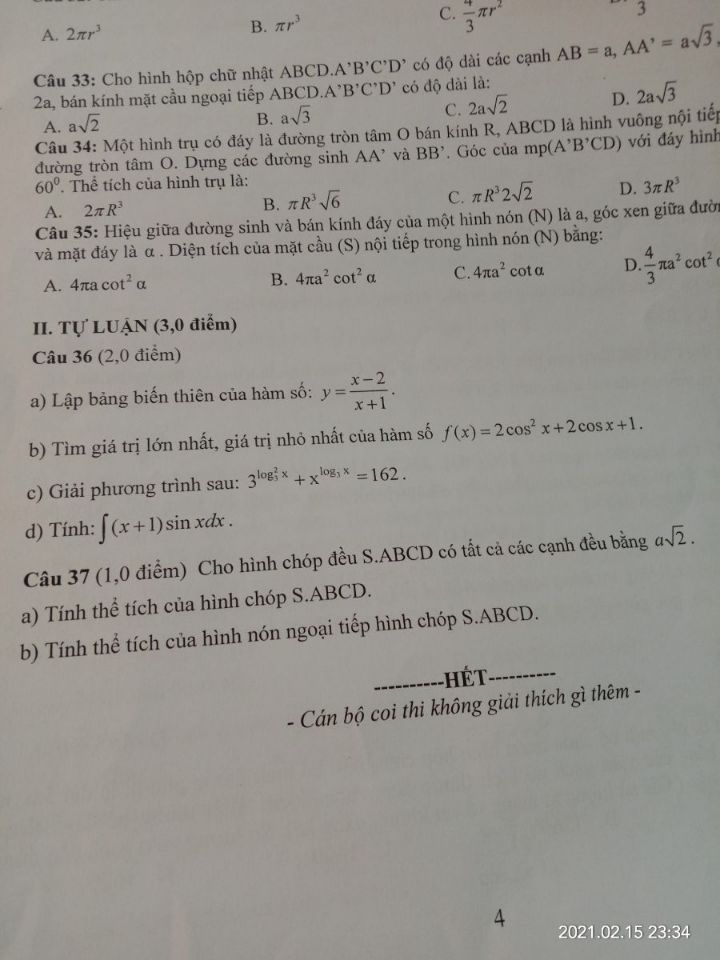 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời
Bài tập SGK khác
Bài tập 1.35 trang 21 SBT Toán 12
Bài tập 1.36 trang 21 SBT Toán 12
Bài tập 1.37 trang 21 SBT Toán 12
Bài tập 1.38 trang 21 SBT Toán 12
Bài tập 1.39 trang 21 SBT Toán 12
Bài tập 1.40 trang 21 SBT Toán 12
Bài tập 1.41 trang 21 SBT Toán 12
Bài tập 1.42 trang 22 SBT Toán 12
Bài tập 1.43 trang 22 SBT Toán 12
Bài tập 1.44 trang 22 SBT Toán 12
Bài tập 1.45 trang 22 SBT Toán 12
Bài tập 1.46 trang 22 SBT Toán 12
Bài tập 16 trang 22 SGK Toán 12 NC
Bài tập 17 trang 22 SGK Toán 12 NC
Bài tập 18 trang 22 SGK Toán 12 NC
Bài tập 19 trang 22 SGK Toán 12 NC
Bài tập 20 trang 22 SGK Toán 12 NC
Bài tập 21 trang 22 SGK Toán 12 NC
Bài tập 22 trang 23 SGK Toán 12 NC
Bài tập 23 trang 23 SGK Toán 12 NC
Bài tập 24 trang 23 SGK Toán 12 NC
Bài tập 25 trang 23 SGK Toán 12 NC
Bài tập 26 trang 23 SGK Toán 12 NC






