Bài học Ôn chương 6 sẽ giúp các em hệ thống lại toàn bộ kiến thức của Cung và góc lượng giác, Công thức lượng giác cũng như phương pháp giải các dạng bài tập liên quan đến lượng giác
1.2. Giá trị lượng giác của \(\alpha \)
1.3. Công thức lượng giác cơ bản
1.6. Công thức nhân đôi - nhân ba - hạ bậc
1.7. Công thức biến đổi tổng thành tích - tích thành tổng
3. Luyện tập bài 4 chương 6 đại số 10
3.1. Trắc nghiệm về Cung và góc lượng giác, công thức lượng giác
3.2. Bài tập SGK & Nâng cao về Cung và góc lượng giác, công thức lượng giác
Tóm tắt lý thuyết
Các kiến thức cần nhớ
1.1. Quan hệ giữa độ và rađian
\({180^ \circ } = \pi {\rm{ }}rad\)
Các góc đặc biệt \(0;\frac{\pi }{6};\frac{\pi }{4};\frac{\pi }{3};\frac{\pi }{2};\pi \)
1.2. Giá trị lượng giác của \(\alpha \)
|
\(\begin{array}{l} \(2.\left| {\sin \alpha } \right| \le 1\;\;\;\;\;\left| {\cos \alpha } \right| \le 1\) |
.PNG) |
1.3. Công thức lượng giác cơ bản
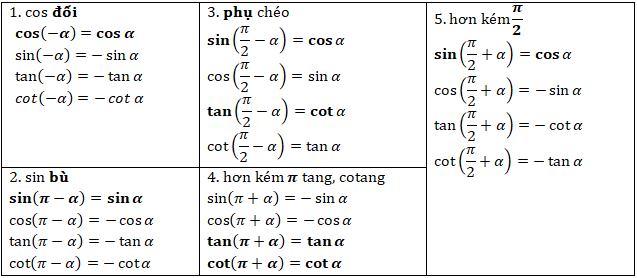
1.4. Công thức cung liên kết
1.5. Công thức cộng
1.6. Công thức nhân đôi - nhân ba - hạ bậc
1.7. Công thức biến đổi tổng thành tích - tích thành tổng
Bài tập minh họa
Dạng 1: Chứng minh đẳng thức lượng giác
1. Phương pháp:
Muốn chứng minh 1 đẳng thức lượng giác, ta dùng công thức lượng giác để biến đổi biểu thức lượng giác ở 1 vế thành biểu thức lượng giác ở vế kia.
Để ý rằng 1 biểu thức lượng giác có thể biến đổi thành nhiều dạng khác nhau. Ví dụ:
\({\sin ^2}2x = 1 - {\cos ^2}2x\) (CT LG cơ bản)
\({\sin ^2}2x = \frac{1}{2}\left( {1 - \cos 4x} \right)\) (CT hạ bậc)
\({\sin ^2}2x = 4{\sin ^2}x.{\cos ^2}x\) (CT nhân đôi)
Tùy theo mỗi bài toán, ta chọn CT thích hợp để biến đổi
2. Ví dụ minh họa
Ví dụ 1: Chứng minh
\(a.\;{\sin ^4}\alpha + {\cos ^4}\alpha = 1 - \frac{1}{2}{\sin ^2}2\alpha \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b.\;{\sin ^6}\alpha + {\cos ^6}\alpha = 1 - \frac{3}{4}{\sin ^2}2\alpha \)
Hướng dẫn: Áp dụng CT LG cơ bản và HĐT \({a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab{\rm{ }}{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\)
\(a.\;{\sin ^4}\alpha + {\cos ^4}\alpha = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha } \right)^2} + {\left( {{\rm{co}}{{\rm{s}}^2}\alpha } \right)^2} = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)^2} - 2{\rm{si}}{{\rm{n}}^2}\alpha .{\rm{co}}{{\rm{s}}^2}\alpha \)
\( = 1 - \frac{1}{2}{\left( {2\sin \alpha .\cos \alpha } \right)^2} = 1 - \frac{1}{2}{\sin ^2}2\alpha \)
\(b.\;{\sin ^6}\alpha + {\cos ^6}\alpha = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha } \right)^3} + {\left( {{\rm{co}}{{\rm{s}}^2}\alpha } \right)^3} = {\left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)^3} - 3{\rm{si}}{{\rm{n}}^2}\alpha .{\rm{co}}{{\rm{s}}^2}\alpha \left( {{\rm{si}}{{\rm{n}}^2}\alpha + {\rm{co}}{{\rm{s}}^2}\alpha } \right)\)
\( = 1 - 3si{n^2}\alpha .co{s^2}\alpha = 1 - \frac{3}{4}{\sin ^2}2\alpha \)
Ví dụ 2: Chứng minh
\(a.\cos 3a.{\rm{si}}{{\rm{n}}^3}a + \sin 3a.{\rm{co}}{{\rm{s}}^3}a = \frac{3}{4}\sin 4a\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b.\;\cos 3a.{\rm{co}}{{\rm{s}}^3}a + \sin 3a.{\rm{si}}{{\rm{n}}^3}a = {\rm{co}}{{\rm{s}}^3}2a\)
Hướng dẫn: Áp dụng CT nhân ba – CT cộng \(4{\rm{si}}{{\rm{n}}^3}a = 3\sin a - \sin 3a\;\;\;\;\;\;\;4{\rm{co}}{{\rm{s}}^3}a = \cos 3a + 3\cos a\)
\(\begin{array}{l}
a.\cos 3a.{\rm{si}}{{\rm{n}}^3}a + \sin 3a.{\rm{co}}{{\rm{s}}^3}a = \cos 3a\frac{{3\sin a - \sin 3a}}{4} + \sin 3a\frac{{\cos 3a + 3\cos a}}{4}\\
= \frac{1}{4}\left[ {\cos 3a\left( {3\sin a - \sin 3a} \right) + \sin 3a\left( {\cos 3a + 3\cos a} \right)} \right]\\
= \frac{1}{4}\left( {3\sin a.\cos 3a - \cos 3a.\sin 3a + \sin 3a.\cos 3a + 3.\cos a.\sin 3a} \right)\\
= \frac{3}{4}\left( {\sin a.\cos 3a + \cos a.\sin 3a} \right) = \frac{3}{4}\sin \left( {a + 3a} \right) = \frac{3}{4}\sin 4a
\end{array}\)
\(\begin{array}{l}
b.\cos 3a.{\rm{co}}{{\rm{s}}^3}a + \sin 3a.{\rm{si}}{{\rm{n}}^3}a = \frac{1}{4}\left[ {\cos 3a\left( {\cos 3a + 3\cos a} \right) + \sin 3a\left( {3\sin a - \sin 3a} \right)} \right]\\
= \frac{1}{4}\left( {{\rm{co}}{{\rm{s}}^3}3a + 3\cos 3a.\cos a + 3.\sin a.\sin 3a - {\rm{si}}{{\rm{n}}^3}3a} \right)\\
= \frac{1}{4}\left[ {{\rm{co}}{{\rm{s}}^3}3a - {\rm{si}}{{\rm{n}}^3}3a + 3\left( {\cos 3a.\cos a + \sin a.\sin 3a} \right)} \right]\\
= \frac{1}{4}\left[ {\cos 6a + 3\cos \left( {3a - a} \right)} \right]\\
= \frac{1}{4}\left( {4{\rm{co}}{{\rm{s}}^3}2a - 3\cos 2a + 3\cos 2a} \right) = {\rm{co}}{{\rm{s}}^3}2a
\end{array}\)
Ví dụ 3: Chứng minh
\(\begin{array}{l}
a.\sin \left( {a + b} \right).\sin \left( {a - b} \right) = {\rm{co}}{{\rm{s}}^2}a - {\rm{co}}{{\rm{s}}^2}b\;\\
b.\sin x.\sin \left( {\frac{\pi }{3} - x} \right).\sin \left( {\frac{\pi }{3} + x} \right) = \frac{1}{4}\sin 3x\\
c.\tan x.\tan \left( {\frac{\pi }{3} - x} \right).\tan \left( {\frac{\pi }{3} + x} \right) = \tan 3x\;\;\;\;\;\;\;\;\;\;\;\;\;
\end{array}\)
Hướng dẫn: Áp dụng CT biến đổi tích thành tổng
\(a.\sin \left( {a + b} \right).\sin \left( {a - b} \right) = \frac{1}{2}\left( {\cos 2b - \cos 2a} \right) = \frac{1}{2}\left[ {2{{\cos }^2}b - 1 - \left( {2{{\cos }^2}a - 1} \right)} \right] = {\rm{co}}{{\rm{s}}^2}b - {\rm{co}}{{\rm{s}}^2}a\)
\(\begin{array}{l}
b.\sin x.\sin \left( {\frac{\pi }{3} - x} \right).\sin \left( {\frac{\pi }{3} + x} \right) = \frac{1}{2}\sin x\left( {\cos 2x - \cos \frac{{2\pi }}{3}} \right) = \frac{1}{2}\sin x.\cos 2x - \frac{1}{4}\sin x\\
= \frac{1}{4}\left( {\sin 3x - \sin x} \right) - \frac{1}{4}\sin x = \frac{1}{4}\sin 3x
\end{array}\)
\(\begin{array}{l}
c.\tan x.\tan \left( {\frac{\pi }{3} - x} \right).\tan \left( {\frac{\pi }{3} + x} \right) = \tan x.\frac{{\tan \frac{\pi }{3} - \tan x}}{{1 + \tan \frac{\pi }{3}.\tan x}}.\frac{{\tan \frac{\pi }{3} + \tan x}}{{1 - \tan \frac{\pi }{3}.\tan x}}\\
= \tan x.\frac{{\sqrt 3 - \tan x}}{{1 + \sqrt 3 \tan x}}.\frac{{\sqrt 3 + \tan x}}{{1 - \sqrt 3 \tan x}}\\
= \tan x.\frac{{3 - {{\tan }^2}x}}{{1 - 3{{\tan }^2}x}} = \tan 3x
\end{array}\)
Dạng 2: Rút gọn, tính giá trị của 1 biểu thức lượng giác
1. Phương pháp
Muốn rút gọn 1 biểu thức lượng giác, ta dung các CTLG để biến đổi biểu thức đã cho.
Muốn tính giá trị của 1 biểu thức lượng giác, ta tìm cách rút gọn biểu thức này. Ngoài việc dùng các CTLG, nên xem xét biểu thức đã cho có dạng gì đặc biệt, từ đó chọn cách giải thích hợp.
2. Ví dụ minh họa
Ví dụ 1: Rút gọn các biểu thức sau
\(\begin{array}{l}
a.A = \;\sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \cos \left( {\frac{{2\pi }}{3} - x} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\
b.\;B = \cos x + \cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right)
\end{array}\)
Hướng dẫn: Áp dụng CT cung phụ - CT biến đổi tổng thành tích – tích thành tổng
a. Ta có \(\;\frac{{2\pi }}{3} - x = \frac{\pi }{2} - \left( {x - \frac{\pi }{6}} \right) \Rightarrow \cos \left( {\frac{{2\pi }}{3} - x} \right) = \cos \left[ {\frac{\pi }{2} - \left( {x - \frac{\pi }{6}} \right)} \right] = \sin \left( {x - \frac{\pi }{6}} \right)\)
\(\begin{array}{l}
A = \;\sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \cos \left( {\frac{{2\pi }}{3} - x} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\\
= \sin \left( {2x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) - \sin \left( {x - \frac{\pi }{6}} \right).\cos \left( {2x + \frac{\pi }{3}} \right)\\
= \sin \left[ {\left( {2x + \frac{\pi }{3}} \right) - \left( {x - \frac{\pi }{6}} \right)} \right] = \sin \left( {x + \frac{\pi }{2}} \right) = \cos x
\end{array}\)
\(\begin{array}{l}
b. B = \cos x + \cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right)\\
= \cos x + \left[ {\cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x - \frac{{2\pi }}{3}} \right)} \right]\\
= \cos x + 2\cos x.\cos \frac{{2\pi }}{3} = \cos x + 2\cos x.\left( { - \frac{1}{2}} \right)\\
= \cos x - \cos x = 0
\end{array}\)
Ví dụ 2: Chứng minh các biểu thức sau không phụ vào:
\(\begin{array}{l}
a.\;A = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\\
b.\;B = {\cos ^2}x + {\cos ^2}\left( {x + a} \right) - 2\cos a.\cos x.\cos \left( {x + a} \right)\\
c.\;C = {\cos ^2}x + {\sin ^2}\left( {x + a} \right) - 2\sin a.\cos x.\sin \left( {x + a} \right)
\end{array}\)
Hướng dẫn: Áp dụng CT biến đổi tổng thành tích – tích thành tổng và HĐT
\(\begin{array}{l}
a.\;A = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\\
= 3{\sin ^4}x + 3{\cos ^4}x - 2\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\left( {{{\sin }^4}x - {{\sin }^2}x.{{\cos }^2}x + {{\cos }^4}x} \right)\\
= 3{\sin ^4}x + 3{\cos ^4}x - 2{\sin ^4}x + 2{\sin ^2}x.{\cos ^2}x - 2{\cos ^4}x\\
= {\sin ^4}x + 2{\sin ^2}x.{\cos ^2}x + {\cos ^4}x\\
= {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} = 1,\;\forall x
\end{array}\)
Vậy A không phụ thuộc vào x
\(\begin{array}{l}
b.\;B = {\cos ^2}x + {\cos ^2}\left( {x + a} \right) - \cos a.\left[ {2\cos x.\cos \left( {x + a} \right)} \right]\\
= \frac{1}{2}\left( {1 + \cos 2x} \right) + \frac{1}{2}\left[ {1 + \cos \left( {2x + 2a} \right)} \right] - \cos a\left[ {\cos \left( {2x + a} \right) + \cos a} \right]\\
= 1 + \frac{1}{2}\left[ {\cos 2x + \cos \left( {2x + 2a} \right)} \right] - \cos a.\cos \left( {2x + a} \right) - {\cos ^2}a\\
= 1 + \cos a.\cos \left( {2x + a} \right) - \cos a.\cos \left( {2x + a} \right) - {\cos ^2}a\\
= 1 - {\cos ^2}a = {\sin ^2}a,\;\forall x
\end{array}\)
Vậy B không phụ thuộc vào x
\(\begin{array}{l}
c.\;C = {\cos ^2}x + {\sin ^2}\left( {x + a} \right) - 2\sin a.\cos x.\sin \left( {x + a} \right)\\
= 1 + \frac{1}{2}\left[ {\cos 2x - \cos \left( {2x + 2a} \right)} \right] - \sin a\left[ {\sin \left( {2x + a} \right) + \sin a} \right]\\
= 1 - \sin \left( {2x + a} \right).\sin \left( { - a} \right) - \sin \left( {2x + a} \right).\sin a - {\sin ^2}a\\
= 1 - {\sin ^2}a = {\cos ^2}a,\;\forall x
\end{array}\)
Vậy C không phụ thuộc vào x
Ví dụ 3: Tính giá trị biểu thức
\(\begin{array}{l}
a.A = \frac{1}{{\sin 10^\circ }} - 4\sin 70^\circ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\
b.\;B = \sin 20^\circ .\sin 40^\circ .\sin 80^\circ \\
c.C = \cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9} + \cos \frac{{7\pi }}{9}\;
\end{array}\)
Hướng dẫn: Áp dụng CT phụ - CT tổng thành tích–tích thành tổng
\(\begin{array}{l}
a.A = \frac{1}{{\sin 10^\circ }} - 4\sin 70^\circ = \frac{1}{{\sin 10^\circ }} - 4\cos 20^\circ = \frac{{1 - 4\cos 20^\circ .\sin 10^\circ }}{{\sin 10^\circ }}\\
= \frac{{1 - 2\left( {\cos 30^\circ - \sin 10^\circ } \right)}}{{\sin 10^\circ }} = \frac{{2\sin 10^\circ }}{{\sin 10^\circ }} = 2
\end{array}\)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
b.\;B = \sin {20^^\circ }.\sin {40^^\circ }.\sin {80^^\circ }\\
= \frac{1}{2}\sin {20^^\circ }\left( {\cos {{40}^^\circ } - \cos {{120}^^\circ }} \right)\\
= \frac{1}{2}\sin {20^^\circ }.\cos {40^^\circ } + \frac{1}{4}\sin {20^^\circ }
\end{array}\\
\begin{array}{l}
= \frac{1}{4}\left( {\sin {{60}^^\circ } - \sin {{20}^^\circ }} \right) + \frac{1}{4}\sin {20^^\circ }\\
= \frac{1}{4}\sin {60^^\circ } = \frac{{\sqrt 3 }}{8}
\end{array}
\end{array}\)
\(c.C = \cos \frac{\pi }{9} + \left( {\cos \frac{{5\pi }}{9} + \cos \frac{{7\pi }}{9}} \right) = \cos \frac{\pi }{9} + 2\cos \frac{{6\pi }}{9}.\cos \frac{\pi }{9} = \cos \frac{\pi }{9} - \cos \frac{\pi }{9} = 0\)
3. Luyện tập Bài 4 chương 6 đại số 10
Bài học Ôn chương 6 sẽ giúp các em hệ thống lại toàn bộ kiến thức của Cung và góc lượng giác, Công thức lượng giác cũng như phương pháp giải các dạng bài tập liên quan đến lượng giác
3.1 Trắc nghiệm về cung và góc lượng giác, công thức lượng giác
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Ôn tập chương VI - Toán 10 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. \(\cos \alpha = \;\frac{1}{2}\;;\;\;\sin \alpha = \;\frac{{\sqrt 3 }}{2}\;;\quad \tan \alpha \; = \;\sqrt 3 \;;\;\;\cot \alpha = \;\frac{1}{{\sqrt 3 }}\)
- B. \(\cos \alpha = \; - \frac{1}{2}\;;\;\;\sin \alpha = \; - \frac{{\sqrt 3 }}{2}\;;\quad \tan \alpha \; = \; - \sqrt 3 \;;\;\;\cot \alpha = \; - \frac{1}{{\sqrt 3 }}\)
- C. \(\cos \alpha = \; - \frac{{\sqrt 2 }}{2}\;;\;\;\sin \alpha = \;\frac{{\sqrt 2 }}{2}\;;\quad \tan \alpha \; = \; - 1\;;\;\;\cot \alpha = \; - 1\)
- D. \(\cos \alpha = \;\frac{{\sqrt 3 }}{2}\;;\;\;\sin \alpha = \; - \frac{1}{2}\;;\quad \tan \alpha \; = \; - \frac{1}{{\sqrt 3 }}\;;\;\;\cot \alpha = \; - \sqrt 3 \)
-
- A. \(\frac{1}{{\sin x}}\)
- B. \(\frac{1}{{\cos x}}\)
- C. cosx
- D. sinx
-
- A. \(\frac{1}{{\sin x}}\)
- B. \(\frac{1}{{\cos x}}\)
- C. cosx
- D. sinx
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK và Nâng Cao về cung và góc lượng giác, công thức lượng giác
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Ôn tập chương VI - Toán 10 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
Bài tập 1 trang 155 SGK Đại số 10
Bài tập 2 trang 155 SGK Đại số 10
Bài tập 3 trang 155 SGK Đại số 10
Bài tập 4 trang 155 SGK Đại số 10
Bài tập 5 trang 156 SGK Đại số 10
Bài tập 6 trang 156 SGK Đại số 10
Bài tập 7 trang 156 SGK Đại số 10
Bài tập 8 trang 156 SGK Đại số 10
Bài tập 9 trang 157 SGK Đại số 10
Bài 10 trang 157 SGK Đại số 10
Bài tập 11 trang 157 SGK Đại số 10
Bài tập 12 trang 157 SGK Đại số 10
Bài tập 13 trang 157 SGK Đại số 10
Bài tập 14 trang 157 SGK Đại số 10
Bài tập 6.42 trang 191 SBT Toán 10
Bài tập 6.43 trang 191 SBT Toán 10
Bài tập 6.44 trang 191 SBT Toán 10
Bài tập 6.45 trang 191 SBT Toán 10
Bài tập 6.46 trang 192 SBT Toán 10
Bài tập 6.47 trang 192 SBT Toán 10
Bài tập 6.48 trang 192 SBT Toán 10
Bài tập 6.49 trang 192 SBT Toán 10
Bài tập 6.50 trang 192 SBT Toán 10
Bài tập 6.51 trang 192 SBT Toán 10
Bài tập 6.52 trang 192 SBT Toán 10
Bài tập 6.53 trang 192 SBT Toán 10
Bài tập 6.54 trang 193 SBT Toán 10
Bài tập 6.55 trang 193 SBT Toán 10
Bài tập 6.56 trang 193 SBT Toán 10
Bài tập 6.57 trang 193 SBT Toán 10
Bài tập 6.59 trang 193 SBT Toán 10
Bài tập 6.58 trang 193 SBT Toán 10
Bài tập 55 trang 217 SGK Toán 10 NC
Bài tập 56 trang 218 SGK Toán 10 NC
Bài tập 57 trang 218 SGK Toán 10 NC
Bài tập 58 trang 218 SGK Toán 10 NC
Bài tập 59 trang 218 SGK Toán 10 NC
Bài tập 60 trang 219 SGK Toán 10 NC
Bài tập 61 trang 219 SGK Toán 10 NC
Bài tập 62 trang 219 SGK Toán 10 NC
Bài tập 63 trang 219 SGK Toán 10 NC
Bài tập 64 trang 219 SGK Toán 10 NC
Bài tập 65 trang 219 SGK Toán 10 NC
Bài tập 66 trang 219 SGK Toán 10 NC
Bài tập 67 trang 220 SGK Toán 10 NC
Bài tập 68 trang 220 SGK Toán 10 NC
Bài tập 69 trang 220 SGK Toán 10 NC
4. Hỏi đáp về bài 4 chương 6 đại số 10
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 10 HỌC247





.PNG)
.PNG)
.PNG)
.PNG)





