Toán 11 Ôn tập chương 5 Đạo hàm

Lý thuyết10 Trắc nghiệm48 BT SGK 290 FAQ

Nội dung bài Ôn tập chương V Đạo hàm sẽ giúp các em hệ thống những nội dung kiến thức trọng tâm của toàn chương từ đó làm nền tảng để các em có thể giải được các bài tập từ cơ bản đến nâng cao. Đạo hàm là kiến thức nền tảng phục vụ cho chương trình Giải tích 12, nên đòi hỏi các em phải học thật tốt chương này và ghi nhớ được các công thức tính đạo hàm.

YOMEDIA

1. Tóm tắt lý thuyết

1.1. Hệ thống kiến thức chương V Đại số và Giải tích 11

1.2. Các công thức tính đạo hàm

2. Bài tập minh hoạ

3. Luyện tập bài 6 chương 5 giải tích 11

3.1. Trắc nghiệm về Đạo hàm

3.2. Bài tập SGK & Nâng cao về Đạo hàm

4. Hỏi đáp về bài 6 chương 5 giải tích 11

Tóm tắt lý thuyết

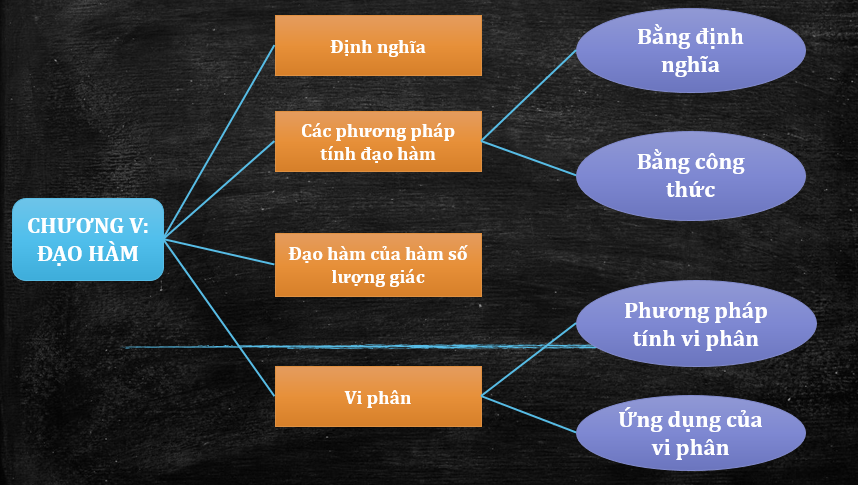
1.1. Hệ thống kiến thức chương V Đại số và Giải tích 11

Hệ thống kiến thức chương đạo hàm

Hình 1: Hệ thống kiến thức chương đạo hàm

1.2. Các công thức tính đạo hàm

BẢNG 1: CÁC CÔNG THỨC ĐẠO HÀM LỚP 11

Hàm số	Hàm hợp tương ứng
\({\left( C \right)^\prime } = 0\,\,\,\,\,;\,\,\,\,{\left( x \right)^\prime } = 1\)
\({\left( {{x^n}} \right)^\prime } = n.{x^{n - 1}}\,\,\left( {n \in \mathbb{N}\,\,,\,\,n \ge 2} \right)\)	\({\left( {{u^n}} \right)^\prime } = n.{u^{n - 1}}.u'\,\,\,\,\,,\,\,\,\left( {n \in \mathbb{N}\,\,,\,\,n \ge 2} \right)\)
\({\left( {\sqrt x } \right)^\prime } = \frac{1}{{2\sqrt x }}\,\,\,\,,\,\,\left( {x > 0} \right)\)	\(\,\,\,{\left( {\sqrt u } \right)^\prime } = \frac{{u'\,}}{{2\sqrt u }}\,\,\,\,\,,\,\,\left( {u > 0} \right)\)
\({\left( {\sin x} \right)^\prime } = \cos x\,\,\,\)	\({\left( {\sin u} \right)^\prime } = u.'\cos u\)
\({\left( {\cos x} \right)^\prime } = - \sin x\,\)	\({\left( {\cos u} \right)^\prime } = - u'.\sin u\)
\({\left( {\tan x} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\,\,\)	\(\,\,{\left( {\tan u} \right)^\prime } = \frac{{u'}}{{{{\cos }^2}u}}\,\)
\({\left( {\cot x} \right)^\prime } = - \frac{1}{{{{\sin }^2}x}}\,\,\)	\(\,\,{\left( {\cot u} \right)^\prime } = - \frac{{u'}}{{{{\sin }^2}u}}\,\)

Bài tập minh họa

Ví dụ 1: Tính đạo hàm các hàm số sau:

a) \(y = {x^3} - 2{x^2} + 3x + 4\) b) \(y = \sin x - \cos x + \tan x\)

c) \(y = {x^4} + 2\sqrt x \) d) \(y = \cot x - 3x + 2\)

Hướng dẫn:

a) \(y' = \left( {{x^3} - 2{x^2} + 3x + 4} \right)' = 3{x^2} - 4x + 3\)

b) \(y' = \left( {\sin x - \cos x + \tan x} \right)' = \cos x + \sin x + \frac{1}{{{{\cos }^2}x}}\)

c) \(y' = \left( {{x^4} + 2\sqrt x } \right)' = 4{x^3} + \frac{1}{{\sqrt x }}\)

d) \(y' = \left( {\cot x - 3x + 2} \right)' = - \frac{1}{{{{\sin }^2}x}} - 3\)

Ví dụ 2: Tính đạo hàm các hàm số tại các điểm tương ứng

a) \(y = - {x^3} + 3{x^2} - 4x + 1\) tại \({x_0} = - 1\)

b) \(y = \sin 2x + \cos x\) tại \({x_0} = - \frac{\pi }{4}\)

c) \(y = \sqrt x - 2x\) tại \({x_0} = 2\)

Hướng dẫn:

\(\begin{array}{l}
a) y' = \left( { - {x^3} + 3{x^2} - 4x + 1} \right)' = - 3{x^2} + 6x - 4\\
\Rightarrow y'\left( { - 1} \right) = - 3 - 6 - 4 = - 13
\end{array}\)

\(\begin{array}{l}
b) y' = \left( {\sin 2x + \cos x} \right)' = 2\cos 2x - \sin x\\
\Rightarrow y'\left( { - \frac{\pi }{4}} \right) = 2\cos \left( { - \frac{\pi }{2}} \right) - \sin \left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}
\end{array}\)

\(\begin{array}{l}
c) y' = \left( {\sqrt x - 2x} \right)' = \frac{1}{{2\sqrt x }} - 2\\
\Rightarrow y'\left( 2 \right) = \frac{1}{{2\sqrt 2 }} - 2 = \frac{{1 - 4\sqrt 2 }}{{2\sqrt 2 }}
\end{array}\)

Ví dụ 3: Tính đạo hàm các hàm số

\(\begin{array}{l}
{\rm{a) }}y = \frac{{{x^2} + 3x - 1}}{{x + 1}}\\
{\rm{b) }}y = \sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)\\
{\rm{c) }}y = \sqrt {{x^2} + 4x + 1} \\
{\rm{d) }}y = \tan \left( {{x^2} + 2\sqrt x + 1} \right)
\end{array}\)

Hướng dẫn:

a) \({\rm{ }}y' = \left( {\frac{{{x^2} + 3x - 1}}{{x + 1}}} \right)' = \frac{{\left( {2x + 3} \right)\left( {x + 1} \right) - \left( {{x^2} + 3x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x + 4}}{{{{\left( {x + 1} \right)}^2}}}\)

b) \(y' = \left( {\sin \left( {2x + 1} \right) + \cos \left( {1 - x} \right)} \right)' = 2\cos \left( {2x + 1} \right) + \sin \left( {1 - x} \right)\)

c) \(y' = \left( {\sqrt {{x^2} + 4x + 1} } \right)' = \frac{{2x + 4}}{{2\sqrt {{x^2} + 4x + 1} }} = \frac{{x + 2}}{{\sqrt {{x^2} + 4x + 1} }}\)

\(\begin{array}{l}
d) y' = \left( {\tan \left( {{x^2} + 2\sqrt x + 1} \right)} \right)' = \frac{{\left( {{x^2} + 2\sqrt x + 1} \right)'}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}\\
= \frac{{2x + \frac{1}{{\sqrt x }}}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}} = \frac{{2x\sqrt x + 1}}{{{\rm{co}}{{\rm{s}}^2}\left( {{x^2} + 2\sqrt x + 1} \right)}}
\end{array}\)

Ví dụ 4: Chứng minh \(y' + 2{y^2} + 2 = 0\) với \(y = \cot 2x\)

Hướng dẫn:

Ta có \(y' = - \frac{2}{{{{\sin }^2}2x}}\)

Khi đó \(y' + 2{y^2} + 2 = - \frac{2}{{{{\sin }^2}2x}} + \frac{{2{{\cos }^2}2x}}{{{{\sin }^2}2x}} + 2 = \frac{{ - 2 + 2\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right)}}{{{{\sin }^2}2x}} = 0\) (đpcm)

3. Luyện tập Bài 6 chương 5 giải tích 11

Trên đây, bài viết đã giới thiệu đến các em những nội dung kiến thức trọng tâm của chương V Đại số và Giải tích 11. Từ đó làm nền tảng để các em có thể giải được các bài tập từ cơ bản đến nâng cao.

3.1 Trắc nghiệm về Đạo hàm

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Ôn tập chương V - Toán 11 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Đạo hàm của hàm số f(t)=a³t⁴-2at²+3t-5a bằng biểu thức nào sau đây?
- A. 4a³t³-4at+3
- B. 3a² t⁴-2t²-5
- C. 12a²t³-4at-2
- D. 4a³t³-4at-5
Câu 2:
Đạo hàm của hàm số \(y = \frac{{2{x^2} - 3x + 4}}{{ - 2x + 1}}\) bằng biểu thức nào sau đây?
- A. \(\frac{{ - 4{x^2} + 4x + 5}}{{ - 2x + 1}}\)
- B. \(\frac{{ - 4{x^2} + 4x + 5}}{{{{\left( { - 2x + 1} \right)}^2}}}\)
- C. \(\frac{{ - 12{x^2} + 16x - 11}}{{{{\left( { - 2x + 1} \right)}^2}}}\)
- D. \(\frac{{ - 6{x^2} + 7x + 1}}{{{{\left( { - 2x + 1} \right)}^2}}}\)
Câu 3:
Đạo hàm cuả hàm số \(y = \left( {\frac{3}{x} - 2x} \right)\left( {\sqrt x - 4} \right)\) bằng biểu thức nào sau đây?
- A. \(\frac{{ - 3}}{{2x\sqrt x }} - 3\sqrt x + \frac{{12}}{{{x^2}}} + 8\)
- B. \(\frac{{ - 9}}{{2x\sqrt x }} - \sqrt x + \frac{{12}}{{{x^2}}} + 8\)
- C. \(\frac{{ - 3}}{{2x\sqrt x }} + 3\sqrt x + \frac{{12}}{{{x^2}}} + 8\)
- D. \(\frac{3}{{2x\sqrt x }} + 3\sqrt x + \frac{{12}}{{{x^2}}} + 8\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK và Nâng Cao về Đạo hàm

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Ôn tập chương V - Toán 11 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 11 Cơ bản và Nâng cao.

Bài tập 1 trang 176 SGK Đại số & Giải tích 11

Bài tập 2 trang 176 SGK Đại số & Giải tích 11

Bài tập 3 trang 176 SGK Đại số & Giải tích 11

Bài tập 4 trang 176 SGK Đại số & Giải tích 11

Bài tập 5 trang 176 SGK Đại số & Giải tích 11

Bài tập 6 trang 176 SGK Đại số & Giải tích 11

Bài tập 7 trang 176 SGK Đại số & Giải tích 11

Bài tập 8 trang 177 SGK Đại số & Giải tích 11

Bài tập 9 trang 177 SGK Đại số & Giải tích 11

Bài tập 10 trang 177 SGK Đại số & Giải tích 11

Bài tập 11 trang 177 SGK Đại số & Giải tích 11

Bài tập 12 trang 177 SGK Đại số & Giải tích 11