Bài tập 52 trang 221 SGK Toán 11 NC
Tính vi phân của hàm số \(y = \frac{1}{{{{(1 + tanx)}^2}}}\) tại điểm \(x = \frac{\pi }{6}\) ứng với \(\Delta x = \frac{\pi }{{360}}\) (tính chính xác đến hàng phần vạn).
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
df(x) = \frac{{ - 2(1 + \tan x)\frac{1}{{{{\cos }^2}x}}}}{{{{(1 + \tan x)}^4}}}.\Delta x\\
= \frac{{ - 2\Delta x}}{{{{\cos }^2}x{{(1 + \tan x)}^3}}}
\end{array}\)
\(\begin{array}{l}
\Rightarrow df(\pi 6) = \frac{{ - 2.\frac{\pi }{{360}}}}{{{{\cos }^2}\frac{\pi }{6}{{\left( {1 + \tan \frac{\pi }{6}} \right)}^3}}}\\
= \frac{{ - \pi }}{{180.\frac{3}{4}{{\left( {1 + \frac{1}{{\sqrt 3 }}} \right)}^3}}} \approx - 0,0059
\end{array}\)
-- Mod Toán 11 HỌC247
-


Tính tích a.b sao cho hàm số có đạo hàm trên R?
bởi Ngọc Hương
 29/05/2020
29/05/2020
Giúp mình câu 10 với ạ
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Số đường thẳng đi qua điểm A(2;0) và tiếp xúc với đồ thị (C) của hàm số y=-x^4+2x^2
bởi nhun
 11/05/2020
11/05/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


a) Cho hàm số y = xsinx. Chứng minh x.yn-2(y'-sinx) + xy = 0
b) Cho hàm số y =
chứng minh y3.yn + 1 =0
Theo dõi (0) 0 Trả lời -


Chứng minh y'^2+4y^2=4 với y=sin2x
bởi Cherry Dao
 09/05/2020
09/05/2020
y'2+4y2=4 với y=sin2x
Theo dõi (0) 1 Trả lời -


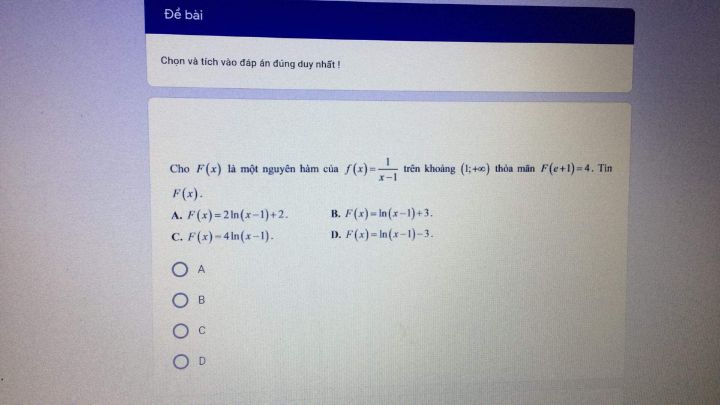
Tìm nguyên hàm F(x) của f(x)=1/(x-1) trên khoảng (1;+∞) thỏa mãn F(e+1)=4
bởi Truong Hai Anh
 10/03/2020
10/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính đạo hàm y=-cosx/sin^3x+4/3cotx
bởi Nhi Vân
 30/07/2019
Giúp m câu i với ạ
30/07/2019
Giúp m câu i với ạ Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Viết phương trình tiếp tuyến của (C): y= x^3 - 3x biết tiếp tuyến tạo với d: y= x+1
bởi Phạm Thanh Tâm
 13/04/2019
13/04/2019
các bạn giúp mình câu này với
viết pt tiếp tuyến của (C): y= X3 - 3X. biết tiếp tuyến tạo với d: y= X+1 góc þ, cos Þ= 5/căn 41
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 50 trang 221 SGK Toán 11 NC
Bài tập 51 trang 221 SGK Toán 11 NC
Bài tập 53 trang 221 SGK Toán 11 NC
Bài tập 54 trang 221 SGK Toán 11 NC
Bài tập 55 trang 221 SGK Toán 11 NC
Bài tập 56 trang 221 SGK Toán 11 NC
Bài tập 57 trang 222 SGK Toán 11 NC
Bài tập 58 trang 222 SGK Toán 11 NC
Bài tập 59 trang 222 SGK Toán 11 NC
Bài tập 60 trang 222 SGK Toán 11 NC
Bài tập 61 trang 222 SGK Toán 11 NC





