Bài tập 56 trang 221 SGK Toán 11 NC
Cho parabol (P) : y = x2. Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = - 2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
Hướng dẫn giải chi tiết
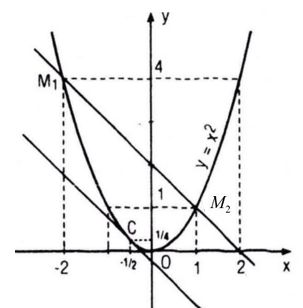
Các điểm M1 và M2 có tọa độ là M1(-2 ; 4); M2(1 ; 1)
Hệ số góc của cát tuyến M1M2 là
\(tan\varphi = \frac{{\Delta y}}{{\Delta x}} = \frac{{4 - 1}}{{ - 2 - 1}} = - 1\)
Vì tiếp tuyến tại điểm \(C({x_0};x_0^2)\) song song với cát tuyến M1M2 nên ta có :
y′(x0) = −1 ⇔ 2x0 = −1 ⇔ x0 = −1/2
Suy ra tọa độ của điểm C là (−1/2; 1/4)
Vậy phương trình tiếp tuyến phải tìm là:
\(y = ( - 1)\left( {x + \frac{1}{2}} \right) + \frac{1}{4} \Leftrightarrow y = - x - \frac{1}{4}\)
-- Mod Toán 11 HỌC247
-
Viết phương trình tiếp tuyến của đồ thị (C). Biết tiếp tuyến đó vuông góc với đường thẳng (d) \(y=\frac{8}{27}x +1\)
bởi Nguyễn Hạ Lan
08/02/2017
Cho hàm số \(y=\frac{x^3}{2}-\frac{3}{4}x^2-3x+\frac{1}{2} (1)\). Viết phương trình tiếp tuyến của đồ thị (C). Biết tiếp tuyến đó vuông góc với đường thẳng (d)
\(y=\frac{8}{27}x +1\)Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x + 5
bởi can tu
08/02/2017
Cho hàm số \(\small y=-x^3+3x^2\). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x + 5.
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị hàm số (C) biết tiếp tuyến có hệ số góc k = 9
bởi Aser Aser
07/02/2017
Cho hàm số \(y=x^3-3x^2+1\) có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C) biết tiếp tuyến có hệ số góc k = 9
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ thỏa mãn f''(x) = 18
bởi na na
08/02/2017
Cho hàm số \(y=f(x)=-x^3+6x^2-9x+2\) có đồ thị là (C). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ thỏa mãn f''(x) = 18.
Theo dõi (0) 1 Trả lời -
Tìm tọa độ điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M và hai trục tọa độ tạo thành một tam giác cân
bởi Bin Nguyễn
07/02/2017
Cho hàm số \(y=\frac{2x-1}{x-1}(1).\) Tìm tọa độ điểm M thuộc (C) sao cho tiếp tuyến của (C) tại M và hai trục tọa độ tạo thành một tam giác cân.
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị (C) tại điểm thuộc đồ thị (C) có tung độ là nghiệm phương trình \(f''(x)-x.f''(x)-6=0\)
bởi Trần Phương Khanh
08/02/2017
Cho hàm số \(y=x^3-6x^2+9x+1\). Viết phương trình tiếp tuyến của đồ thị (C) tại điểm thuộc đồ thị (C) có tung độ là nghiệm phương trình \(f''(x)-x.f''(x)-6=0\)
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến đó có hệ số góc nhỏ nhất
bởi Đặng Ngọc Trâm
08/02/2017
Cho hàm số \(y=2x^{3}-3x^{2}+1\). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến đó có hệ số góc nhỏ nhất.
Theo dõi (0) 1 Trả lời
