Bài tập 51 trang 221 SGK Toán 11 NC
Tìm đạo hàm đến cấp được nêu kèm theo của các hàm số sau (n ϵ N*)
\(\begin{array}{*{20}{l}}
{a)y = \sin x,\:y'''}\\
{b)y = \sin x\sin 5x,{y^{(4)}}}\\
{c)y = {{(4 - x)}^5},{y^{(n)}}}\\
{d)y = \frac{1}{{2 + x}},{y^{(n)}}}\\
{e)y = \frac{1}{{2x + 1}},{y^{(n)}}}\\
{f)y = {{\cos }^2}x,{y^{(2n)}}}
\end{array}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
y\prime = \cos x\\
y = - \sin x\\
y\prime \prime \prime = - \cos x
\end{array}\)
b)
\(\begin{array}{*{20}{l}}
{y = \frac{1}{2}(\cos 4x - \cos 6x)}\\
{y\prime = - 2\sin 4x + 3\sin 6x}\\
{y = - 8\cos 4x + 18\cos 6x}\\
{y\prime = 32\sin 4x - 108\sin 6x}\\
{{y^{(4)}} = 128\cos 4x - 648\cos 6x}
\end{array}\)
c)
\(\begin{array}{l}
y\prime = - 5{(4 - x)^4}\\
y = 20{(4 - x)^3}\\
y\prime = - 60{(4 - x)^2}\\
{y^{(4)}} = 120(4 - x)\\
{y^{(5)}} = - 120\\
{y^{(n)}} = 0(\forall n \ge 6)
\end{array}\)
d)
\(\begin{array}{l}
y = \frac{1}{{x + 2}} = {(x + 2)^{ - 1}}\\
y\prime = - 1{(x + 2)^{ - 2}}\\
y'' = ( - 1)( - 2){(x + 2)^{ - 3}},...
\end{array}\)
Bằng quy nạp ta chứng minh được:
\(\begin{array}{l}
{y^{(n)}} = ( - 1)( - 2)...( - n).{(x + 2)^{ - n - 1}}\\
= {( - 1)^n}.\frac{{n!}}{{{{(x + 2)}^{n + 1}}}}
\end{array}\)
e)
\(\begin{array}{l}
y = {(2x + 1)^{ - 1}}\\
y\prime = ( - 1)(2{(2x + 1)^{ - 2}})\\
y'' = ( - 1)( - 2){.2^2}{(2x + 1)^{ - 3}},...
\end{array}\)
Bằng quy nạp ta chứng minh được:
\({y^{(n)}} = {( - 1)^n}.\frac{{{2^n}.n!}}{{{{(2x + 1)}^{n + 1}}}}\)
f)
\(\begin{array}{*{20}{l}}
{y\prime = - \sin 2x}\\
{y = - 2\cos 2x}\\
{y''' = {2^2}\sin 2x}\\
{{y^{(4)}} = {2^3}\cos 2x}\\
{{y^{(5)}} = - {2^4}\sin 2x}\\
{{y^{(6)}} = - {2^5}\cos 2x,...}
\end{array}\)
Bằng quy nạp ta chứng minh được:
\({y^{(2n)}} = {( - 1)^n}{.22^{n - 1}}\cos 2x\)
-- Mod Toán 11 HỌC247
-


Chứng minh rằng : 4xy+ 2sin2x +xy’’=2y’ với y=x.sin2x?
bởi Đức
 18/06/2020
18/06/2020
Cho hàm số y=x.sin2x. Chứng minh rằng : 4xy+ 2sin2x +xy’’=2y’
Theo dõi (0) 1 Trả lời -


Chứng minh rằng hàm số sau thỏa mãn hệ thức?
bởi Băng Trần Châu
 17/06/2020
17/06/2020
Bài 7 ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để phương trình \(y = \frac{2}{3}{x^3} - \left( {m + 1} \right){x^2} + 3\left( {m + 1} \right) + 2\) có hai nghiệm trái dấu?
bởi Băng Trần Châu
 14/06/2020
14/06/2020
Giúp mình câu b với
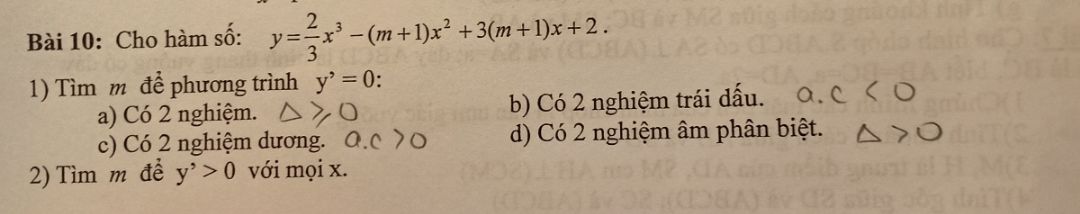 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


giúp mình y=căn(x^2-1). giải phương trình xy'=1
Theo dõi (1) 0 Trả lời -


Tính đạo hàm \(y = 3{x^{ - 3}} - 3x + 2\)?
bởi Nguyễn Trung Hiếu
 09/06/2020
09/06/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 là bao nhiêu?
bởi minh hải
 08/06/2020
08/06/2020
Giúp mình với ạ!
Cho hàm số y=f(x) có đạo hàm liên tục trên R, thỏa mãn \(2f(2x) + f(1 - 2x) = 12{x^2}\). Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 là?
Theo dõi (0) 0 Trả lời -


Toạ độ điểm M là bao nhiêu?
bởi Thản Lương
 01/06/2020
01/06/2020
Giải giùm em bài này với ạ
Cho hàm số y= (2x +1)/(x-1) có đồ thị (c). Gọi d là tiếp tuyến của (c), biết d đi qua điểm A(4;-1). Gọi M là tiếp điểm của d và (c), toạ độ điểm M là bao nhiêu?
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 49 trang 220 SGK Toán 11 NC
Bài tập 50 trang 221 SGK Toán 11 NC
Bài tập 52 trang 221 SGK Toán 11 NC
Bài tập 53 trang 221 SGK Toán 11 NC
Bài tập 54 trang 221 SGK Toán 11 NC
Bài tập 55 trang 221 SGK Toán 11 NC
Bài tập 56 trang 221 SGK Toán 11 NC
Bài tập 57 trang 222 SGK Toán 11 NC
Bài tập 58 trang 222 SGK Toán 11 NC
Bài tập 59 trang 222 SGK Toán 11 NC
Bài tập 60 trang 222 SGK Toán 11 NC
Bài tập 61 trang 222 SGK Toán 11 NC





