Bài tập 50 trang 221 SGK Toán 11 NC
a. Chứng minh rằng \(\left( {\frac{1}{{{x^n}}}} \right)\prime = - \frac{n}{{{x^{n + 1}}}},\) trong đó n ϵ N*
b. Với x ≠ 0 và n ϵ N*, ta đặt \({x^{ - n}} = \frac{1}{{{x^n}}}\). Từ đó hãy so sánh đẳng thức trong câu a với công thức \({\left( {{x^n}} \right)^\prime } = n{x^{n - 1}}\) và nêu nhận xét.
Hướng dẫn giải chi tiết
a) Ta có:
\(\left( {\frac{1}{{{x^n}}}} \right)' = \frac{{ - ({x^n})\prime }}{{{x^{2n}}}} = \frac{{ - n{x^{n - 1}}}}{{{x^{2n}}}} = - \frac{n}{{{x^{n + 1}}}}\)
b) Ta có: \(({x^{ - n}})\prime = - n{x^{ - n - 1}}\) (theo câu a)
Nhận xét : Công thức \(({x^n})\prime = - n{x^{n - 1}}\) đúng với mọi giá trị nguyên của n (chú ý rằng khi n ≤ 0 thì chỉ có thể xét đạo hàm trên \(( - \infty ;0) \cup (0; + \infty )\))
-- Mod Toán 11 HỌC247
-


Tính đạo hàm của hàm số sau: \(\displaystyle y = ({2 \over x} + 3x)(\sqrt x - 1)\)
bởi thu hảo
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Tính đạo hàm của hàm số sau: \(\displaystyle y = {{3{x^2} - 6x + 7} \over {4x}}\)
bởi Thuy Kim
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Tính đạo hàm của hàm số sau: \(\displaystyle y = {2 \over x} - {4 \over {{x^2}}} + {5 \over {{x^3}}} - {6 \over {7{x^4}}}\)
bởi minh thuận
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Tính đạo hàm của hàm số sau: \(y = {{{x^3}} \over 3} - {{{x^2}} \over 2} + x - 5\)
bởi Lê Tấn Vũ
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính đạo hàm của hàm số sau:
bởi Hoàng Nguyễn Thúy Vân
 26/06/2020
26/06/2020
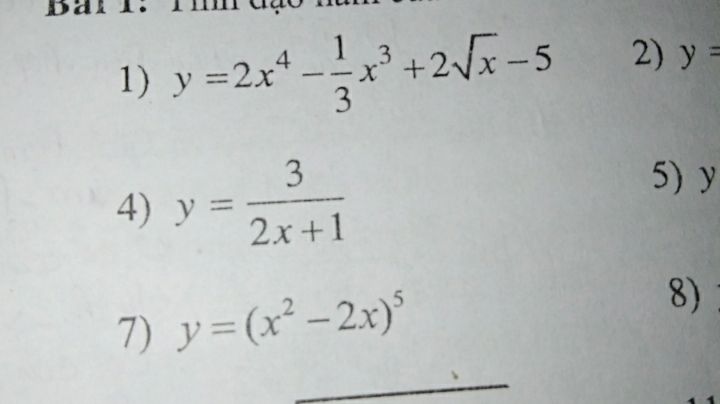 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm đạo hàm cấp 2n của y=sin3x?
bởi Mỹ Linh
 23/06/2020
giúp mình voiTheo dõi (0) 0 Trả lời
23/06/2020
giúp mình voiTheo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 5.131 trang 219 SBT Toán 11
Bài tập 49 trang 220 SGK Toán 11 NC
Bài tập 51 trang 221 SGK Toán 11 NC
Bài tập 52 trang 221 SGK Toán 11 NC
Bài tập 53 trang 221 SGK Toán 11 NC
Bài tập 54 trang 221 SGK Toán 11 NC
Bài tập 55 trang 221 SGK Toán 11 NC
Bài tập 56 trang 221 SGK Toán 11 NC
Bài tập 57 trang 222 SGK Toán 11 NC
Bài tập 58 trang 222 SGK Toán 11 NC
Bài tập 59 trang 222 SGK Toán 11 NC
Bài tập 60 trang 222 SGK Toán 11 NC
Bài tập 61 trang 222 SGK Toán 11 NC





