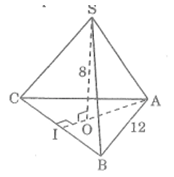
Bài tập 58 trang 149 SBT Toán 8 Tập 2
Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước trên hình vẽ.
Hướng dẫn giải chi tiết
Hình vẽ đã cho là hình chóp có 3 mặt xung quanh và mặt đáy là tam giác đều bằng nhau có cạnh là a.Áp dụng định lí pi-ta-go vào tam giác vuông CIA, ta có: AC2 = AI2 + CI2
Suy ra: CI2 = AC2 – AI2 = \({a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\)
Vậy CI = \(\frac{{a\sqrt 3 }}{2}\)
Ta có: \({S_{ABC}} = \frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{4}\)(đvdt)
Vậy \({S_{tp}} = 4.\frac{{{a^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \) (đvdt)
-- Mod Toán 8 HỌC247
-


Tìm x để x^4-x^2+2x+2 là số chính phương
bởi Nguyễn Lê Thảo Trang
 26/02/2019
26/02/2019
Tìm x để \(x^4-x^2+2x+2\) là số chính phương
Theo dõi (0) 1 Trả lời -


Chứng minh 2^51-1 chia hết cho 7
bởi Lê Tấn Thanh
 26/02/2019
26/02/2019
cm 251-1 chia het cho7
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2+1)^2+3x(x^2+1)+2x^2=0
bởi Phan Thị Trinh
 26/02/2019
26/02/2019
Giải phương trình:
(x2+1)2+3x(x2+1)+2x2=0
Theo dõi (0) 1 Trả lời -


Rút gọn 7x^2 +14x +7/ 3x^2 + 3x
bởi Bi do
 26/02/2019
26/02/2019
rút gọn
a) 7x^2 +14x +7/ 3x^2 + 3x
b) 2a^2 - 20ab / ac + ad - bc - bd
c) x^2 - xy / y^2 - x^2Theo dõi (0) 1 Trả lời -


Tính GTNN của A=x^2+2y^2 biết x+2y=1
bởi Thanh Truc
 26/02/2019
26/02/2019
Cho x+2y=1.Tính GTNN của A=x^2+2y^2
Theo dõi (0) 1 Trả lời -


Chứng minh 8^5+2^11 chia hết cho 17
bởi My Le
 26/02/2019
26/02/2019
CM: \(8^5+2^{11}\)chia hết cho 17
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2 + x)^2 + 4(x^2 + x) = 12
bởi thu trang
 26/02/2019
26/02/2019
Bài 1: (3đ)Phân tích đa thức x3 – 5x2 + 8x – 4 thành nhân tử
Bài 2: (3đ) Giải các phương trình sau:
(x2 + x)2 + 4(x2 + x) = 12
Bài 3: (2đ) Cho hình vuông ABCD; Trên tia đối tia BA lấy E, trên tia đối tia CB lấy F sao cho AE = CF
a) Chứng minh EDF vuông cân
b) Gọi O là giao điểm của 2 đường chéo AC và BD. Gọi I là trung điểm EF. Chứng minh O, C, I thẳng hàng.
Bài 4: (2)Cho tam giác ABC vuông cân tại A. Các điểm D, E theo thứ tự di chuyển trên AB, AC sao cho BD = AE. Xác địnhvị trí điểm D, E sao cho:
a/ DE có độ dài nhỏ nhất
b/ Tứ giác BDEC có diện tích nhỏ nhất.
Theo dõi (0) 1 Trả lời -


Tìm x biết x^2-4x+8=2x-1
bởi thanh duy
 26/02/2019
26/02/2019
x^2-4x+8=2x-1
Tìm x
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của đa thức P=2x-x^2
bởi Dương Quá
 26/02/2019
26/02/2019
Tìm giá trị lớn nhất của đa thức:
\(P=2x-x^2\)
\(Q=1-x-x^2\)
Theo dõi (0) 1 Trả lời -


Tìm các cặp số nguyên x, y sao cho x^2 + 102 = y^2
bởi Nhat nheo
 26/02/2019
26/02/2019
Tìm các cặp số nguyên x ; y sao cho: x2 + 102 = y2
Theo dõi (0) 1 Trả lời -


Chứng minh n^3+(n+1)^3+(n+2)^3 chia hết cho 9
bởi Thùy Nguyễn
 26/02/2019
26/02/2019
C/m : \(n^3+\left(n+1\right)^3+\left(n+2\right)^3\) \(⋮\) \(9\) \(\forall n\in N\) \(\ne0\)
Theo dõi (0) 1 Trả lời -


Giải bất phương trình (m^2+1)x+1
bởi Nguyễn Thị An
 26/02/2019
26/02/2019
Giải bpt
(m2+1)x+1<m
Theo dõi (0) 1 Trả lời -


Phân tích (x+y)^2 - ( x-y)^2 thành nhân tử
bởi Lan Ha
 26/02/2019
26/02/2019
Bài : Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức:
(x+y)2 - ( x-y)2
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x(x-2016) - x+2016=0
bởi Thanh Nguyên
 26/02/2019
26/02/2019
Tìm x, biết:
a) 2x(x-2016) - x+2016=0
b)(x+2)2-(x-2)(x+2)=0
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của 2x^2 + x + 1
bởi thi trang
 26/02/2019
26/02/2019
Tìm giá trị nhỏ nhất của 2x2 + x + 1
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^3+ x^2+x thành nhân tử
bởi Nguyễn Thị An
 26/02/2019
26/02/2019
Câu 1: phân tích đa thức thành nhân tử
a, x3+ x2+x b, xy + y2-x-y
Câu 2: tìm x biết
a, 3x(x2-4)=0 b,2x2-x-6=0
Câu 3: tính giả thiết của đẳng thức
P=x(x-y)+y(x+y) tại x=6, y=-8
Câu 4: Tính chia
(x3+x2=2x):(x+2)Theo dõi (0) 1 Trả lời -


Tính 27-x^3/5x+5 : 2x-6/3x+3
bởi Phạm Hoàng Thị Trà Giang
 26/02/2019
26/02/2019
bài 3:
a) 27-x3/5x+5 : 2x-6/3x+3
b) (4x2-16) : 3x+6/7x-2
c) 3x3+3/x-1 : (x2-x+1)
d) 4x+6y/x-1 : 4x2+12xy+9y2/1-x3
Theo dõi (0) 1 Trả lời -


Tìm x biết |2-x|=0,5x-4
bởi Nguyễn Bảo Trâm
 26/02/2019
26/02/2019
|2-x|=0,5x-4
|x+2|=2x-10
Theo dõi (0) 1 Trả lời -


Phân tích đa thức 4x^4 + 81 thành nhân tử
bởi trang lan
 26/02/2019
26/02/2019
Phân tích đa thức thành nhân tử :
a) 4x4 + 81
b) x7 + x2 + 1
Theo dõi (0) 1 Trả lời -


Thực hiện phép tính 5x/x-1+-5/x-1
bởi Lê Minh Bảo Bảo
 26/02/2019
26/02/2019
thực hiện phép tính
a.5x/x-1+-5/x-1
b.1/x-3+2/x+3+9-x/x2-9
c.4x+8/4-x2.(x2-2x)
Theo dõi (0) 1 Trả lời -


Giải phương trình (x-2)(x+2)-(2x+1)^2 =x(2-3x)
bởi Lê Gia Bảo
 26/02/2019
26/02/2019
Giải các pt sau :
(x-2)(x+2)-(2x+1)2 =x(2-3x)
#tick_3_bạn_nhanh_nhất
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức A = -x^2 - 4x +1
bởi Hoa Hong
 26/02/2019
26/02/2019
Tìm GTLN của:
A = -x2 - 4x +1
B = -2(x+1)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A=x^3-8/x-2
bởi bich thu
 26/02/2019
26/02/2019
Cho A=\(\dfrac{x^3-8}{x-2}\)
Tìm GTNN của A
Theo dõi (0) 1 Trả lời -


Chứng minh n^3+6n^2+8n chia hết cho 48
bởi May May
 26/02/2019
26/02/2019
+Chứng minh:
\(n^3+6n^2+8n\text{ }⋮\text{ }48\text{ }\left(n\text{ }ch\text{ẵn}\right)\)Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A = x^2 - 4x + 15
bởi Dell dell
 26/02/2019
26/02/2019
Tìm GTNN của :
A = x2 - 4x + 15
B = x.(x - 3x)
C = x2 + y2 +4x + 6y +20
Theo dõi (0) 1 Trả lời -


Chứng minh a.(a-1)-(a+3)(a+2) chia hết cho 6
bởi Thụy Mây
 26/02/2019
26/02/2019
Bài 1: Cmr
a, a.(a-1)-(a+3)(a+2):hết cho 6
b,a.(a+2)-(a-7).(a-5):cho 7
c,cho a.(b+1)+b.(a+1)=(a+1)(b+1) .Cm a.b=1
Theo dõi (0) 1 Trả lời -


Tìm x biết 4x(x-5)-(x-1)(4x-3)=5
bởi Spider man
 26/02/2019
26/02/2019
tim x:
a)4x(x-5)-(x-1)(4x-3)=5
b)(3x-4)(x-2)=3x(x-9)-3
c)x^2-81=0
d)3x^2-75=0
e)x^2-14x+3=0
minh can gap. thank you
Theo dõi (0) 1 Trả lời -


Tìm a sao cho (27x^2+a) chia hết cho 3x+2
bởi Nguyễn Minh Minh
 26/02/2019
26/02/2019
Tìm a sao cho:
a) \(\left(27x^2+a\right)⋮\left(3x+2\right)\)
b) \(\left(x^4+ax^2+1\right)⋮\left(x^2+2x+1\right)\)
c) \(\left(3x^2+ã+27\right)\) chia cho x+5 dư 2
Theo dõi (0) 1 Trả lời -


Tính x^2/x^4+x^2+1 biết x/x^2-x+1=1/5
bởi Nguyễn Hoài Thương
 26/02/2019
26/02/2019
Cho \(\dfrac{x}{x^2-x+1}=\dfrac{1}{5}\). Tính \(\dfrac{x^2}{x^4+x^2+1}\)
Theo dõi (0) 1 Trả lời -


Tìm x biết x/7=6/x+1
bởi Sam sung
 26/02/2019
26/02/2019
Câu 1: Tìm x
\(\dfrac{x}{7}=\dfrac{6}{x+1}\)
Giúp mik gấp nhá!
Thank you very much!
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A=x^2+4x+4/x
bởi truc lam
 26/02/2019
26/02/2019
A=\(\dfrac{x^2+4x+4}{x}\) \(\left(x>0\right)\). Tìm giá trị nhỏ nhất.
B=\(\dfrac{x^2}{x-1}\)\(\left(x>1\right)\). Tìm giá trị nhỏ nhất.
Giải bằng cách dùng bất đẳng thức cô si giùm mk nhé ^_^
Theo dõi (0) 1 Trả lời -


Giải phương trình (x-2)(x+2)-(2x+102 =x(2-3x)
bởi Nguyễn Hiền
 26/02/2019
26/02/2019
Giải pt :
(x-2)(x+2)-(2x+102 =x(2-3x)
<có tick cho 3 bạn nhanh nhất>
Theo dõi (0) 1 Trả lời -


Chứng minh a^2+b^2 >= 2ab
bởi Xuan Xuan
 26/02/2019
26/02/2019
Chứng minh:
a) \(a^2+b^2\ge2ab\)
b) \(a^2+b^2+c^2\ge ab+ac+bc\)
c) Cho a, b, c >0. Chứng minh \(a^3+b^3+c^3\ge3abc\). Dấu bằng xảy ra khi nào?
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức M=x^2+5y^2+2xy-2y+2017
bởi Nguyễn Thị Lưu
 26/02/2019
26/02/2019
Tìm GTNN của
M=x^2+5y^2+2xy-2y+2017
Theo dõi (0) 1 Trả lời -


Tìm số nguyên x, y thỏa mãn x^3+2x^2+3x+2 =y^3
bởi Thanh Nguyên
 26/02/2019
26/02/2019
Tìm số nguyên x,y thỏa mãn
x3+2x2+3x+2 =y3
Theo dõi (0) 1 Trả lời -


Tìm x biết x^4-4x^3+3x^2+4x-4=0
bởi cuc trang
 26/02/2019
26/02/2019
tìm x:
\(1,x^4-4x^3+3x^2+4x-4=0\)
\(2,x^2-3x+2=0\)
Theo dõi (0) 1 Trả lời -


Tính 1.2.3+2.3.4+3.4.5+.....+2013.2014.2015
bởi Bin Nguyễn
 26/02/2019
26/02/2019
Bài 1. Tính: \(1.2.3+2.3.4+3.4.5+.....+2013.2014.2015\)
Bài 2. Cho đa thức \(M=\left(a^2+b^2-c^2\right)^2-4a^2b^2\)
a) Phân tích đa thức ra nhân tử
b) Chứng minh rằng nếu a, b, c là số đo các cạnh của tam giác thì M < 0.Theo dõi (0) 1 Trả lời -


Chứng minh a^7-a chia hết cho 7
bởi hành thư
 26/02/2019
26/02/2019
+Chứng minh:
\(a^7-a\text{ }⋮\text{ }7\text{ }\left(a\in Z\right)\)Theo dõi (0) 1 Trả lời -


Chứng minh nếu (a+b+c) chia hết cho 4 thì P chia hết cho 4 biết P=(a+b)(b+c)(c+a)-abc
bởi Lê Minh Trí
 26/02/2019
26/02/2019
Cho P=(a+b)(b+c)(c+a)-abc
CMR nếu (a+b+c) chia hết cho 4 thì P chia hết cho 4
Theo dõi (0) 1 Trả lời -


Phân tích đa thức 2x^2-6x thành nhân tử
bởi Hong Van
 26/02/2019
26/02/2019
phân tích đa thức sau thành nhân tử
a.2x^2-6x
b.2x^2-18
c.x^3+3x^2+x+3
d.x^2-y^2+6y-9
Theo dõi (0) 1 Trả lời -


Chứng minh a^2+b^2+c^2 >= 3/4
bởi thuy linh
 26/02/2019
26/02/2019
Cho cac so a,b,c thoa man: a+b+c=\(\dfrac{3}{2}\)
CMR: \(a^2+b^2+c^2\ge\dfrac{3}{4}\)
Theo dõi (0) 1 Trả lời -


Bai 1 ; Giai phuong trinh
(x3 - x2) - 4x2 + 8x - 4 = 0Theo dõi (0) 1 Trả lời -


Chứng minh a^3-a chia hết cho 3
bởi Nguyễn Vân
 26/02/2019
26/02/2019
+Chứng minh:
\(a^3-a\text{ }⋮\text{ }3\text{ }\left(a\in Z\right)\)Theo dõi (0) 1 Trả lời -


Phân tích đa thức 5x^2-20x+20-5y^2 thành nhân tử
bởi Nguyễn Thị Trang
 26/02/2019
26/02/2019
a)5x2-20x+20-5y2
b)(x-y+5)2-2(x-y+5)+1
c)7x-7y+5x-5y
d)16x2-8x+1
e)100x2-(x2+25)2
chỉ dùm e vs em cần gấp
Theo dõi (0) 1 Trả lời -


Tính GTBT P=2x^6+3x^3y^3+y^3+y^6 biết x^3+y^3=1
bởi Bình Nguyen
 26/02/2019
26/02/2019
Cho\(x^3+y^3=1\). Tính giá trị của biểu thức P= \(2x^6+3x^3y^{^{ }3}+y^3+y^6\)
Theo dõi (0) 1 Trả lời -


Tìm các số nguyên n để 2n^2+n-7 chia hết cho n-2
bởi Bảo Lộc
 26/02/2019
26/02/2019
Tim tat ca cac so nguyen n de: \(2n^2+n-7\) chia het cho n-2
Theo dõi (0) 1 Trả lời -


Chứng minh a/ b+c + b/ c+a + c/ a+b >=2 biết a,b,c > 0
bởi Hoa Hong
 26/02/2019
26/02/2019
CMR: với a,b,c > 0
a/ b+c + b/ c+a + c/ a+b >=2
Theo dõi (0) 1 Trả lời -


Phân tích đa thức 27a^3-1 thành nhân tử
bởi Anh Trần
 26/02/2019
26/02/2019
1. Phân tích đa thức thành nhân tử :
a) 27a\(^3\) - 1
b) 5x\(^2\) - 5xy - 7x + 7y
c) 2x - 2y + ã - ay
2 . Tìm x :
a) 3x\(^2\) - 3x + x - 1 = 0
b) x\(^2\) - 4x + 4 = 1 .
3. Cho hình thang ABCD có BC//AD , góc D = 60độ , AC vuông góc CD , AC là tia phân giác của góc BAD .
a) Tính góc A , gócB , góc C ?
b) Gỉa sử BC = 3cm . Tính chu vi hình thang ABCD .
HELP ME !!!!!!!!!!~ CÁC BẠN NÊU 7 HẰNG ĐẲNG THỨC ĐÃ ÁP DỤNG VÀO TỪNG CÂU NHA !
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của thương (4x^5 + 2x^4 + 4x^3 -x-1) chia hết cho 2x^3+x-1
bởi Thùy Trang
 26/02/2019
26/02/2019
Tìm giá trị nhỏ nhất của thương
(4x5 + 2x4 + 4x3 - x -1):(2x3+x-1)
Theo dõi (0) 1 Trả lời -


Thực hiện phép nhân 5x(3x^2-4x+1)
bởi Bin Nguyễn
 26/02/2019
26/02/2019
Câu 1: Thực hiện phép nhân
a. \(5x.\left(3x^2-4x+1\right)\)
b. \(\left(x+3\right)\left(x^2+3x-5\right)\)
Câu 2: Phân tích ĐT thành NT
a. \(2x^2-4x\)
b. \(x^2-2xy+y^2-9\)
c. \(x^2+x-6\)
Câu 3: Cho biểu thức: \(A=\dfrac{1}{x+2}-\dfrac{1}{x-2}+\dfrac{2x}{x^2-4}\)
a. Tìm ĐKXĐ
b. Rút gọn A
c. Tính giá trị của A khi \(x=\dfrac{1}{2}\)
Câu 4: Cho tam giác ABC cân tại A, có đường cao AH. Gọi I là trung điểm của AC, K là điểm đối xứng của H qua I.
a. Chứng mình rằng tứ giác AHCK là HCN
b. Biết AH = 12cm, HC = 5cm. Tính diện tích HCN AHCK và tính chu vi tam giác ABC.
c. Tìm điều kiện của tam giác ABC để tứ giác AHCK là hình vuông.
Câu 5: Cho đa thức \(f\left(x\right)=x^{2016}+x^{2015}+x^{200}+x^2\)
Tìm đa thức dư trong phép chia \(f\left(x\right):\left(x^2-1\right)\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 6x - 2(3+x) - 4(x+3) = 0
bởi Ban Mai
 26/02/2019
26/02/2019
Giải phương trình sau: 6x - 2(3+x) - 4(x+3) = 0
Theo dõi (0) 1 Trả lời -


Chứng minh ab + ac + bc < a^ + b^2 + c^2 < 2(ab+ac+bc)
bởi Thụy Mây
 26/02/2019
26/02/2019
Cho a,b,c là 3 cạnh của 1 tam giác. Chứng minh ab + ac + bc < a2 + b2 + c2 < 2(ab+ac+bc).
Ai biết giải thì giúp mình với mình xin cảm ơnTheo dõi (0) 1 Trả lời -


Giải phương trình 2x^2-x-1/2-3x^2+x+4=(5-x)(2x+4)
bởi Lê Viết Khánh
 26/02/2019
26/02/2019
Giải phương trình:
a) \(\dfrac{2x^2-x-1}{2}-3x^2+x+4=\left(5-x\right)\left(2x+4\right)\)
b) \(\dfrac{\left(2x-5\right)\left(3x+7\right)}{4}+2x-1=\dfrac{\left(x-1\right)\left(2x+4\right)}{2}+1\)
c) 8x3 - 1 = 8x2 + 4x + 2
d) (x2 + x + 1)(x2 - x + 1) = x6 - 1
e) (x3 + 2x)(x2 + 4) = (x4 + 6x2 + 8)(3 - 2x)
f) \(\dfrac{x+97}{125}+\dfrac{x-63}{35}=\dfrac{x-7}{21}+\dfrac{x-27}{49}\)
Giúp mình với!!! Mình cần gấp!!! Câu nào cũng được nhe!!!
Theo dõi (1) 1 Trả lời -


Tìm a nguyên để a^3-2a^2+7a-7 chia hết cho a^2+3
bởi Hong Van
 26/02/2019
26/02/2019
Tìm a nguyên để:
\(a^3-2a^2+7a-7⋮a^2+3\)
Theo dõi (0) 1 Trả lời -


Tìm max của biểu thức A=-x^2 -4x+6
bởi Nguyễn Anh Hưng
 26/02/2019
26/02/2019
tìm max
A=-x2 -4x+6
B= -x2 +2x+2
C= -3x2 -6x-4
D=-2x2+5x+7
E= 5-x2+2x-4y2-4y
Theo dõi (0) 1 Trả lời -


Phân tích đa thức sau thành nhân tử:
(x + 2)(x + 3)(x + 4)(x + 5) - 24
Theo dõi (0) 1 Trả lời -


Chứng minh A = x^2 - 3x + 5 > 0
bởi Nguyễn Xuân Ngạn
 26/02/2019
26/02/2019
B1: Cho A = x2 - 3x + 5
a) Chứng minh A > 0 với mọi x
b) Tìm giá trị nhỏ nhất của A
B2: Tìm cặp (x;y) thỏa mãn:
a) x2 - 6x + y2 - 4y +13 = 0
b) 4x2 - 4x + y2 + 6y + 10 = 0
B3: Cho Q = x2 - 6x + y2 - 2x + 13
a) Chứng minh Q > 0 với mọi x;y
b) Tìm x;y để Q đạt giá trị nhỏ nhất.
~~ GIÚP vớI!!!!!!!!! Mk gấp lắm rùi!!!!!!!
~~~ Tks trước ạ!
Theo dõi (0) 1 Trả lời -


Tìm min của E=2x^2 +3x+4
bởi Ngoc Nga
 26/02/2019
26/02/2019
tìm min
E=2x2 +3x+4
F= x2 -2x+y2-4y+7
Theo dõi (0) 1 Trả lời -


1) Tính giá trị của đa thức
a) P(x) = x7 - 80x6 + 80x5 - 80x4 +...+ 80x + 15 với x = 79
b) Q(x) = x14 - 10x13 + 10x12 - 10x11 +...+ 10x2 - 10x + 10 với x = 9
c) R(x) = x4 - 17x3 + 17x2 - 17x + 20 với x = 16
d) S(x) = x10 - 13x9 + 13x8 - 13x7 +...+ 13x2 - 13x + 10 với x = 12
Theo dõi (0) 1 Trả lời -


Tìm x biết x(x-2)+2-x=0
bởi na na
 26/02/2019
26/02/2019
Tìm x biết:
\(x\left(x-2\right)+2-x=0\)
Theo dõi (0) 1 Trả lời -


Chứng minh x^4 - x^3 + 3x^2+ 2x + 2 luôn dương
bởi Nguyễn Thanh Trà
 26/02/2019
26/02/2019
x4 - x3 + 3x2 2x + 2 chứng minh biểu thức luôn dương
Theo dõi (0) 1 Trả lời -


Tìm min của B= x^2 + 10 +29
bởi Ngoc Nga
 26/02/2019
26/02/2019
tìm min
B= x2 + 10 +29
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+1)^4+(x-3)^4=82
bởi Anh Nguyễn
 26/02/2019
26/02/2019
Giải Phương trình:
1) (x+1)4+(x-3)4=82.2) x4-2x3+5x2-2x+1=0.
3) ((29-x)/21)+((27-x)/23)+((25-x)/25)+((23-x)/27)+((21-x)/29)=0
MONG M.N GIÚP MIK NHA. MIK CẢM ƠN NHÌU...
Theo dõi (0) 1 Trả lời -


Tìm số tự nhiên n biết 2^n/32=4
bởi Tram Anh
 26/02/2019
26/02/2019
Tìm số tự nhiên n , biết
a) \(\dfrac{2^n}{32}\) = 4
b) \(^{^{ }}27^n\) . 9\(^n\) = 9\(^{27}\) : 81
Theo dõi (0) 1 Trả lời -


Cho a,b,c là 3 cạnh của 1 tam giác thỏa mãn a3+b3+c3=3abc. CMR tam giác đó là tam giác đều.
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2 +x )2 +4(x^2+x) =12
bởi Dương Quá
 26/02/2019
26/02/2019
Giải các phương trình
(x2 +x )2 +4(x2+x) =12
Theo dõi (0) 1 Trả lời -


So sánh 3^21 và 2^31
bởi Nguyễn Tiểu Ly
 26/02/2019
26/02/2019
So sánh
a) 3^21 và 2^31
b) 32^9 và 16^13
Theo dõi (0) 1 Trả lời -


Giải phương trình |x^2-5x-6|=x^2-x-24
bởi nguyen bao anh
 26/02/2019
26/02/2019
Giải phương trình
\(\left|x^2-5x-6\right|=x^2-x-24\)
Theo dõi (0) 1 Trả lời -


Tìm số tự nhiên n sao cho \(2^n-1⋮7\)
Theo dõi (0) 1 Trả lời -


Tìm x biết (x-4)(x-5)(x-6)(x-7)=1680
bởi Lê Nhật Minh
 26/02/2019
26/02/2019
tìm x:
(x-4)(x-5)(x-6)(x-7)=1680
Theo dõi (0) 1 Trả lời -


Tìm x biết (x-2).(x+3)-x(x+1)=10
bởi Lan Ha
 26/02/2019
26/02/2019
(x-2).(x+3)-x(x+1)=10
Theo dõi (0) 1 Trả lời -


Thực hiện phép tính 2x(x^2-3x+4)
bởi Anh Trần
 26/02/2019
26/02/2019
thực hiện phép tính
a.2x(x^2-3x+4)
b.(x+2)(x-1)
c.(4x^4-2x^3+6x^2):2x
Theo dõi (0) 1 Trả lời -


chứng minh rằng 9x^2 - 12x + 8 luôn luôn dương với mọi x
Theo dõi (0) 1 Trả lời -


Tìm P biết a^2P + 2aP + a^2 = 4
bởi thu hằng
 26/02/2019
26/02/2019
Tìm P biết:
a2P + 2aP + a2 = 4
Tìm GTNN của đa thức:
B= 2x2 - 4x
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2=y(y+1)(y+2)(y+3)
bởi Van Tho
 26/02/2019
26/02/2019
giải phương trình
x2=y(y+1)(y+2)(y+3) với x,y thuộcZ
Theo dõi (0) 1 Trả lời -


Tìm m để đa thức 2x^3 - 5x^2 + 10x -m chia hết cho đa thức 2x - 1
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức 2x^2 + 4x - 1
bởi Aser Aser
 26/02/2019
26/02/2019
Tìm GTNN cûa biêu thuc:
2x2 + 4x - 1
Theo dõi (0) 1 Trả lời -


Tìm x biết (x-1)(2x+3)-x (x-1)=0
bởi Phan Quân
 26/02/2019
26/02/2019
Tìm x, biết:
(x-1)(2x+3)-x (x-1)=0
giúp mk nha mk cần gấp
Theo dõi (0) 1 Trả lời -


Chứng minh phương trình |x^2+3x+20|+|x+3|=0 vô nghiệm
bởi cuc trang
 27/02/2019
27/02/2019
C/m phương trình sau là vô nghiệm
\(\left|x^2+3x+20\right|+\left|x-3\right|=0\)
Theo dõi (0) 1 Trả lời -


Tìm tất cả các số nguyên n để 2n2 +n-7 chia hết cho n-2
Theo dõi (0) 1 Trả lời -


Rút gọn 3(2^2+1)(2^4+1)(2^8+1)(2^16+1)
bởi can tu
 26/02/2019
26/02/2019
a/ 3(22+1)(24+1)(28+1)(216+1)
b/ 3x(x-2)-5x(1-x) -8x(x2-3)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A=x^2+xy+y^2-3x-3y
bởi Thùy Nguyễn
 26/02/2019
26/02/2019
Tìm GTNN:
A=x2+xy+y2-3x-3y
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Làm tính chia (6x^3 - 7x^2 - x + 2) : (2x + 1)
bởi Tuấn Huy
 26/02/2019
26/02/2019
Làm tính chia
a) (6x3 - 7x2 - x + 2) : (2x + 1)
b) (2x4 - 10x3 - x2 + 15x - 3 ) : (2x2 - 3)
b) (x2 - y2 + 6y + 9 ) : (x - y + 3)
Theo dõi (0) 1 Trả lời -


Giải phương trình (m-5)x=m+3 với m=5
bởi Huong Duong
 26/02/2019
26/02/2019
Cho phương trình: (m-5)x=m+3. (m:tham số)
a. Giải phương trình với m=5
b. Tìm m để phương trình có nghiệm duy nhất x thỏa mãn điều kiện x>1
Lam nhanh giup mk nhe
Theo dõi (0) 1 Trả lời -


C/m nếu a^3 +b^3+c^3=3abc thì a+b+c = 0 hoặc a=b=c
Theo dõi (0) 1 Trả lời -


Tính giá trị x^4-12x^3+12x^2-12x+111 tại x=11
bởi Hoàng My
 27/02/2019
27/02/2019
Tính nhanh giá trị của mỗi biểu thức sau:
\(x^4-12x^3+12x^2-12x+111\) tại x =11
Theo dõi (0) 1 Trả lời -


Tìm số dư trong phép chia 97^20021 cho 51
bởi Hoa Lan
 26/02/2019
26/02/2019
Tìm số dư trong phép chia 9720021 cho 51
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức A=2x^2+y^2-2xy-2x+3
bởi Dell dell
 27/02/2019
27/02/2019
Tìm giá trị nhỏ nhất của các biểu thức :
a, \(A=2x^2+y^2-2xy-2x+3\)b, \(B=x^2-2xy+2y^2+2x-10y+17\)
c, \(C=x^2-xy+y^2-2x-2y\)
Theo dõi (0) 1 Trả lời -


Tìm x biết (x-3)^3+3-x =0
bởi Nguyễn Thị Thanh
 27/02/2019
27/02/2019
Tìm x, biết :
(x-3)3+3-x =0Theo dõi (0) 1 Trả lời -


Tìm n để n=8/2n-5 là số nguyên tố
bởi na na
 27/02/2019
27/02/2019
a=\(\dfrac{n+8}{2n-5}\) tìm n để a là một số nguyên tố
Theo dõi (0) 1 Trả lời -


Tìm x biết (2x+1)(4x^2-2x+1)-8x(x^2+2)=17
bởi Lê Tấn Vũ
 26/02/2019
26/02/2019
(2x+1)(4x^2-2x+1)-8x(x^2+2)=17
Theo dõi (0) 1 Trả lời -


Tìm các số tự nhiên n để (n^2-8)2+36 là số nguyên tố
bởi Quế Anh
 26/02/2019
26/02/2019
Tìm các số tự nhiên n để (n2-8)2+36 là số nguyên tố.
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^4 + 64 thành nhân tử
bởi hi hi
 26/02/2019
26/02/2019
Phân tích đa thức thành nhân tử:
x4 + 64
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^2 + 4x + 3 thành nhân tử
bởi thu hảo
 26/02/2019
26/02/2019
Phân tích đa thức thành nhân tử:
x2 + 4x + 3
Theo dõi (0) 1 Trả lời -


tìm GTNN của biểu thức A+2x^2 +2y^2-2xy-2x-2y+2017
Theo dõi (0) 1 Trả lời -


Chứng minh n^2(n+1)+2n(n+1) chia hết cho 6
bởi Chai Chai
 26/02/2019
26/02/2019
1) Thực hiện phép tính
a) (2x+3)^2+(2x-3)^2-(2x+3)(4x-6)+xy
b) (4x^2+4x+1): (2x+1)
2)Phân tích đa thức sau thành nhân tử
x^3-x+3x^2y+3xy^2-y
3) Tìm x
a)4x^2-12x =-9
b) (5-2x)(2x+7) =4x^2-25
c) x^3+27+(x+3)(x-9) =0
d) 4(2x+7)^2-9(x+3)^2=0
4)CMR với mọi số nguyên n thì:
a)n^2(n+1)+2n(n+1) chia hết cho 6
b)(2n-1)^3-(2n-1) chia hết cho 8
c)(n+7)^2-(n-5)^2 chia hết cho 24
Theo dõi (0) 1 Trả lời -


Tính nhanh 101^2, 97.101
bởi Dell dell
 26/02/2019
26/02/2019
Tính nhanh
\(101^2\)
97.103
\(77^2+23^2+77.46\)
\(105^2-5^2\)
Theo dõi (0) 1 Trả lời -


Phân tích đa thức thành nhân tử:
5x2 - 10xy + 5y2 - 20z2
Theo dõi (0) 1 Trả lời -


Tìm số tự nhiên n sao cho n^2+17 là số chính phương
bởi Spider man
 26/02/2019
26/02/2019
Tìm n thuộc N sao cho \(n^2+17\) là số chính phương
Theo dõi (0) 1 Trả lời -


Tìm n để n+8/2n-5 là số chính phương
bởi hi hi
 26/02/2019
26/02/2019
a=\(\dfrac{n+8}{2n-5}\) tìm n để a là một số chính phương
Theo dõi (0) 1 Trả lời -


Tìm x, y thỏa mãn |3x-1| + 2017 | y-2018 | = 0
bởi Chai Chai
 26/02/2019
26/02/2019
I : Tìm x, y thỏa mãn
|3x-1| + 2017 | y-2018 | = 0
Theo dõi (0) 1 Trả lời -


Tìm nghiệm nguyên của phương trình x + y = xy
bởi Thu Hang
 26/02/2019
26/02/2019
Tìm nghiệm nguyên của phương trình:
1. x + y = xy
2. p(x + y) = xy với p nguyên tố
Theo dõi (0) 1 Trả lời -


Tìm ĐKXĐ của x+5/x^2-5x-x+25/2x^2-50=x-5/2x^2+10x
bởi Trieu Tien
 26/02/2019
26/02/2019
1) \(\dfrac{x+5}{x^2-5x}\)- \(\dfrac{x+25}{2x^2-50}\)=\(\dfrac{x-5}{2x^2+10x}\)
a) Tìm ĐkXĐ
b) Giải PT
2)Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm, đường cao AH. Đường pg BD cắt AH tại I ( CD thuộc AC )
a) Tính BC, AD, DC
b, CM tam giác ABD đồng dạng vs tam giác HBI
-> AB. BI = BD .BH
c) Gọi K là t điểm của ID . Tính S tam giác AKD
Theo dõi (0) 1 Trả lời -


Phân tích đa thức thành nhân tử:
x3- x + 3x2y + 3xy2 + y2 - y
Theo dõi (0) 1 Trả lời -


Tính giá trị biểu thức A=3x^2-2x+3y^2-2y+6xy-100
bởi het roi
 27/02/2019
27/02/2019
\(A=3x^2-2x+3y^2-2y+6xy-100\) Tính giá trị biểu thức biết x+y=5
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức 3x-1/(x+1)(x-3) - 1/(x+1)
bởi Trịnh Lan Trinh
 27/02/2019
27/02/2019
3x-1/(x+1)(x-3) - 1/(x+1)
a, rút gọn biểu thức
b, tìm x thuộc Z để A là số nguyên
Theo dõi (0) 1 Trả lời -


Chứng minh:
x2 + 5y2 + 2x - 4xy - 10y + 14 > 0 với mọi x, y.
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^2+6xy+5y^2-5y-x thành nhân tử
bởi Hy Vũ
 27/02/2019
27/02/2019
Phân tích đa thức thành nhân tử \(x^2+6xy+5y^2-5y-x\)
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A=x^2-2x-6
bởi Nguyễn Minh Hải
 26/02/2019
26/02/2019
Tìm GTNN của biểu thức:
A=x\(^2\)-2x-6 E=x\(^2\)-3x
B=4x\(^2\)4x+7 F=4x\(^2\)-+5x
C=9x\(^2\)-6x G=3x\(^2\)-2\(\sqrt{3}\)x
D=x\(^2\)+12x. H=5x\(^2\)-4\(\sqrt{5}\)x+7
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x(x^2 -4)=0
bởi Phan Thiện Hải
 26/02/2019
26/02/2019
tìm x:
a)2x(x2 -4)=0
Theo dõi (0) 1 Trả lời -


x+2/2008 + x+3/2007 + x+4/2006 + x+2028/6 =0
Theo dõi (0) 1 Trả lời -


Tìm giá trị nhỏ nhất của biểu thức Q=x^2+2y^2+2xy-2x+2015
bởi Lê Minh
 26/02/2019
26/02/2019
Tìm giá trị nhỏ nhất của biểu thức
Q=x2+2y2+2xy-2x+2015
Theo dõi (0) 1 Trả lời -


Tìm x biết x^2+4.x.4-9 = 0
bởi My Le
 26/02/2019
26/02/2019
tính x
x2+4.x.4-9 = 0
Theo dõi (0) 1 Trả lời -


Tính M=x+y/x-y biết 2x^2+2y^2=5xy
bởi Hương Lan
 27/02/2019
27/02/2019
Cho x>y>0 và 2x2+2y2=5xy. Tính M=\(\dfrac{x+y}{x-y}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 2x-2017=1
bởi Chai Chai
 26/02/2019
26/02/2019
1/ Giải các phương trình sau:
a.\(2x-2017=1\)
b.\(x\times\left(2x-3\right)+4x-6=0\)
c.\(\dfrac{x+4}{x+1}+\dfrac{x-2}{x}=2\)
2/ Giải bất phương trình: \(3x-8\ge4-x\)
3/ Giải bài toán bằng cách lập phương trình :
Biết rằng tổng của 2 số bằng 125 và số này gấp 4 lần số kia, tìm 2 số đó?
4/ Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm và AH là đường cao (\(H\in BC\)).
a. Chứng minh tam giác ABC đồng dạng với tam giác HBA.Tính tỉ số diện tích của hai tam ABC và HBA.
b.Tính độ dài.
c. Vẽ đường phân giác BE (E\(\in\)AC) của tam giác ABC.Tính đọ dài AE?
Theo dõi (0) 1 Trả lời